Números primos

Conhecemos como número primo o número natural que possui exatamente dois divisores, 1 e ele mesmo. Encontrar números primos não é uma tarefa fácil, pois não existe nenhum método visual de identificar de forma direta se esse número é primo ou não, então, para isso, foi desenvolvido um método que torna essa tarefa um pouco menos difícil, o crivo de Eratóstenes.

O crivo nada mais é que passos que seguimos para encontrar os números que são múltiplos de um número primo e removê-los de uma lista de números, restando somente os números primos. Quando um número não é primo, podemos escrevê-lo como a multiplicação de números primos, processo esse chamado de fatoração.

Leia também: Quais são os subconjuntos dos números naturais?

Tópicos deste artigo

• 1 - O que são números primos?
• 2 - Como identificar um número primo
• 3 - Crivo de Erastóstenes
• 4 - Números primos de 1 a 1000
• 5 - Fatoração
• 6 - Exercícios resolvidos

O que são números primos?

No conjunto dos números naturais, um número é classificado como número primo ou não dependendo da quantidade de divisores que ele possui. Classificamos um número como primo todo número que possui exatamente dois divisores, sendo eles 1 e ele mesmo.

Como identificar um número primo

Para saber se um número é primo ou não, é necessário analisar os seus possíveis divisores.

Exemplos:

a) 5 é um número primo, pois ele é divisível somente por 1 e por 5.

b) 8 não é um número primo, pois, além de ser divisível por 1 e por 8, também é divisível por 2 e 4.

Existe muita dificuldade para verificar se números muito grandes são primos ou não, para isso foram desenvolvidos alguns programas de computadores que fazem essa testagem. Para identificar os números primos em uma sequência de números, utilizamos o crivo Eratóstenes.

Crivo de Erastóstenes

O crivo de Erastóstenes é um método para encontrar números primos em um intervalo de números naturais. Encontraremos, como exemplo, todos os números primos que existem entre 1 e 100, e, para isso, vamos seguir alguns passos. Primeiro construiremos uma lista com todos os números de 1 até 100.

Sabemos que 1 não é primo, pois ele possui somente a si como divisor. Após o 1, vamos encontrar o primeiro número primo, que é o 2. Sabemos que todos os números divisíveis por 2, exceto o próprio 2, não são primos, pois eles possuem mais de dois divisores, logo, vamos retirar da lista todos os números pares.

O número que vem depois do 2 e que ainda está na lista é o 3, que é um número primo, pois possui somente dois divisores. Vamos retirar da lista todos os números múltiplos de 3, pois eles não são primos.

Na lista, o próximo número é o 5, e ele é primo, agora, vamos remover todos os números múltiplos de 5.

Após o 5, o próximo número da lista é o 7, que é um número primo. Retirando os números que são múltiplos de 7, encontraremos a tabela a seguir.

O próximo número da lista é o 11, que é um número primo. Note que não existe nenhum múltiplo de 11 que ainda não tenha sido tirado da lista, sendo assim, os números restantes são todos números primos.

Os números primos entre 1 e 100 são:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 e 97

Veja também: Curiosidades sobre os números

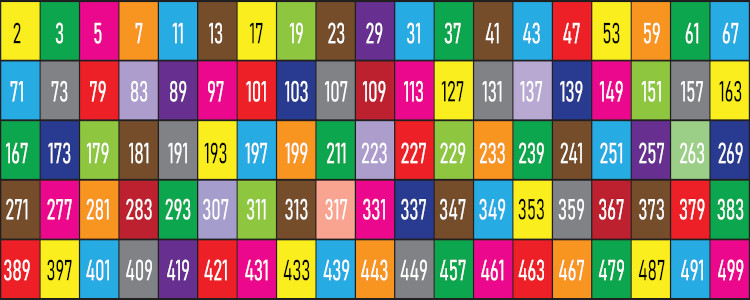
Números primos de 1 a 1000

Todos os números primos que existem entre 1 e 1000.

Fatoração

Quando o número não é primo, podemos escrevê-lo como a multiplicação entre números primos. Essa representação por meio de multiplicação de números primos é conhecida como decomposição em fatores primos. Para encontrar essa decomposição, utilizamos o método da fatoração. Fatorar um número é encontrar os números primos que o dividem.

Exemplo:

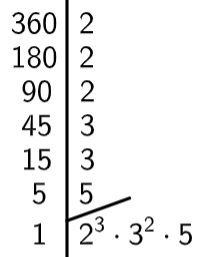
Acesse também: O que são os números reais?

Exercícios resolvidos

Questão 1 – Sobre os números primos, julgue as afirmativas a seguir:

I - Todo número ímpar é primo.

II - Todo número primo é ímpar.

III - O número 2 é o único número primo par.

IV - O menor número primo é o número 1.

Marque a alternativa correta:

A) Somente a afirmativa I é verdadeira.

B) Somente a afirmativa II é verdadeira.

C) Somente a afirmativa III é verdadeira

D) Somente a afirmativa IV é verdadeira.

E) Somente as afirmativas II e IV são verdadeiras.

Resolução

Alternativa C

Analisando as afirmativas, temos que:

I – Falsa. Nem todo número ímpar é primo, por exemplo o 9, que é divisível por 3.

II – Falsa. 2 é um número primo e é par.

III – Verdadeira. 2 é o único número primo par.

IV – Falsa. 1 não é um número primo.

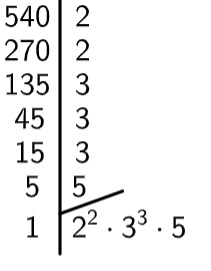
Questão 2 – Sabendo que 540 não é um número primo, marque a alternativa que contém a decomposição em fatores primos correta desse número:

A) 2³· 3² · 5
B) 2² · 3³ · 5² · 7
C) 4 · 9 · 5
D) 2² · 3³ · 5
E) 2 · 3 · 5 · 7

Resolução

Alternativa D