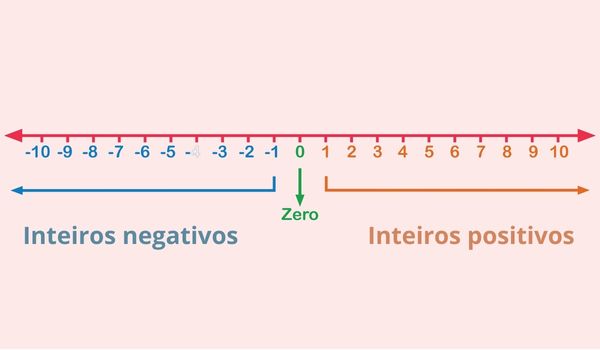
O conjunto dos números inteiros pode ser subdividido em diversos outros conjuntos, que recebem o nome de subconjuntos. Os subconjuntos mais conhecidos dos números inteiros são: Conjunto dos números negativos, conjunto dos números positivos, conjunto dos números pares e conjunto dos números ímpares.
Os números pares e ímpares são identificados por seus algarismos finais: se um número termina nos algarismos 0, 2, 4, 6 e 8 então é considerado par. Se um número termina nos algarismos 1, 3, 5, 7 e 9 é considerado ímpar. Por exemplo, 23 é ímpar pois termina em 3.
Contudo, a definição oficial de “número par” ou “número ímpar” não é essa. Números pares são aqueles que podem ser escritos na forma 2 · n, ou seja, todo número par é resultado de uma multiplicação por 2. Números ímpares são todos aqueles que podem ser escritos na forma 2 · n + 1, ou seja, todo número ímpar é um número par acrescido de uma unidade.
Ao dividir um número por 2, caso o resto seja zero, o número é par, caso o resto seja 1 o número é ímpar.
É possível verificar o que acontece caso operações básicas sejam realizadas entre números pares e/ou ímpares quaisquer. Essa verificação deu origem às seguintes propriedades:
Propriedade 1 – Ao somar ou subtrair dois números pares, o resultado também será par.
Demonstração: Tome os dois números pares 2 · k e 2 · l e some-os
2 · k + 2 · l
2 · (k + l)
Fazendo (k + l) = n teremos o resultado
2 · n
Observe que somando dois números pares o resultado que se obtém é um número par.
Propriedade 2 – A soma ou subtração de dois números ímpares resulta em um número par.
Demonstração: Dados os números ímpares 2 · k +1 e 2 · g + 1,
(2 · k +1) + (2 · g + 1)
2 · k + 2 · g + 2
2 · (k + g + 1)
Fazendo k + g + 1 = n teremos o resultado:
2 · n
Que é um número par!
Propriedade 3 – A multiplicação entre dois números pares terá como resultado um número par.
Demonstração: Dados os números pares 2 · k e 2 · m,
(2 · k) · (2 · m)
4 · k · m
Fazendo k · m = n teremos:
2 · 2 · n
Que é um número par, pois é o produto de um número par (2 · n) por 2.
Propriedade 4 – A multiplicação entre dois números ímpares terá como resultado um número ímpar.
Demonstração: Dados os números ímpares 2 · k + 1 e 2 · g + 1,
(2 · k +1) · (2 · g +1)
4 · k · g + 2 · g + 2 · k + 1
2 (2 · k · g + k + g) + 1
Fazendo (2 · k · g + k + g) = n teremos:
2 · n + 1
Que é um número ímpar.
Propriedade 5 – A soma entre um número par e um número ímpar terá como resultado um número ímpar.
Demonstração: Dados os números 2 · k e 2 · h +1,
2 · k + 2 · h +1
2 · (k + h) + 1
Fazendo k + h = n, teremos:
2 · n + 1
Que é um número ímpar.