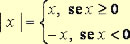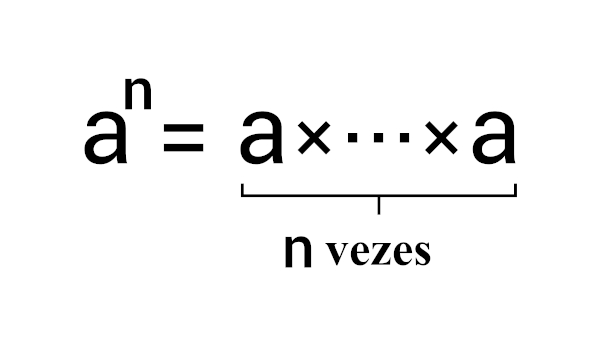Classificamos um número como irracional quando a sua representação decimal é uma dízima não periódica, ou seja, um número decimal infinito não periódico. O que leva esses números a serem conhecidos como irracionais é o fato de que eles não possuem representação fracionária.
São conhecidos como números irracionais as dízimas não periódicas — que são encontradas a partir de raízes não exatas, por exemplo — e também alguns casos particulares, como o π (lê-se: pi).
Leia também: Como resolver operações com conjuntos?
Tópicos deste artigo
- 1 - O que são os números irracionais?
- 2 - Conjunto dos números irracionais
- 3 - Números irracionais e números racionais
- 4 - Operações com números irracionais
- 5 - Exercícios resolvidos
O que são os números irracionais?

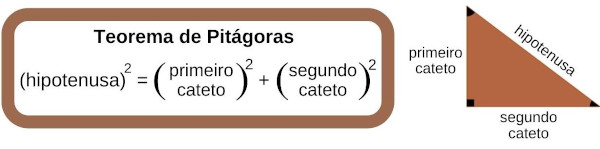
A descoberta dos números irracionais foi feita durante o estudo da geometria. Na tentativa de descobrir o comprimento da hipotenusa de um triângulo que possui lados medindo 1, ao aplicar o teorema de Pitágoras, o resultado encontrado foi um número irracional.
h² = 1² + 1²
h² = 1 + 1
h = √2
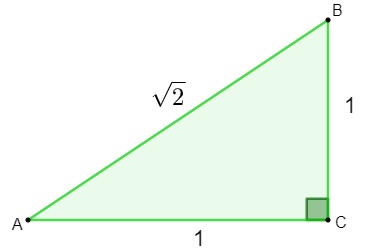
Ao encontrar o número √2, os matemáticos perceberam que esse número não poderia ser classificado como racional, pois não pode ser escrito como uma fração. Surgiu, então, a necessidade da criação e do estudo de um novo conjunto, o conjunto dos números irracionais.
|
Para que um número seja irracional, a sua representação deve ser uma dízima não periódica. Um número irracional não pode ser representado como uma fração. |
Na tentativa de encontrar um número que, multiplicado por ele mesmo, resulte em 2, chegamos a uma dízima não periódica:
√2 = 1,41421356…
Toda raiz não exata é um número irracional.
Exemplos:
-
√3 = 1,7320508…
-
√5 = 2,2360679…
-
√7 = 2,6457513…
-
√8 = 2,8284271…
-
√10 = 3,1622776…
Além das raízes não exatas, qualquer dízima não periódica é um número irracional.
Exemplos:
-
4,123493…
-
0,01230933…
-
2,15141617…
Existem alguns casos especiais de dízimas não periódicas, como o número π, que é encontrado em problemas envolvendo a circunferência, e o número ɸ (lê-se: fi), que é bastante comum em problemas envolvendo proporções na natureza.
π = 3,14159265…
ɸ = 1,61803399…
Leia também: Números primos — números que têm como divisores apenas o 1 e eles mesmos
Conjunto dos números irracionais
Com a descoberta das dízimas não periódicas e a constatação de que esses números não podem ser escritos como uma fração, surgiu um novo conjunto, o conjunto dos números irracionais, que é formado por todos os números cuja representação decimal é uma dízima não periódica.
Para representar o conjunto dos números irracionais, é comum o uso da letra I. Como existem infinitas dízimas periódicas, esse conjunto também é infinito. Da união dos números irracionais com os números racionais surgiu o conjunto dos números reais.
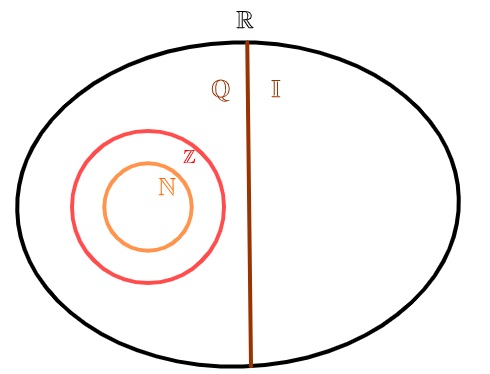
Números irracionais e números racionais
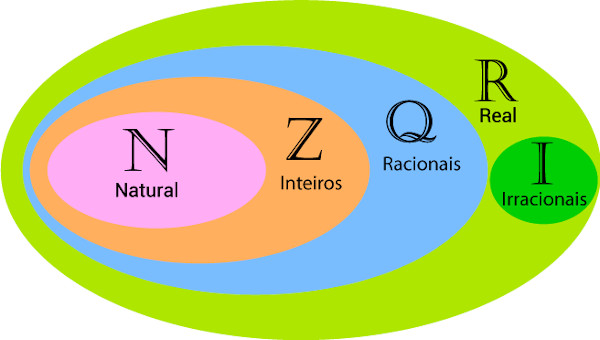
Os números reais podem ser divididos em dois conjuntos: o conjunto dos números racionais e o conjunto dos números irracionais. Diferentemente dos números naturais e inteiros, que são também racionais, o conjunto dos números irracionais não possui nenhum elemento em comum com o conjunto dos números racionais, ou seja, ou um número é racional, ou um número é irracional, mas nunca os dois ao mesmo tempo.
O conjunto dos números racionais é formado por todos os números que podem ser representados como uma fração. Já o conjunto dos números irracionais é formado por números que não podem ser representados como uma fração.
São elementos do conjunto dos números racionais:
- Números inteiros:
{ … – 3, – 2, – 1, 0, 1, 2, 3 …}
- Números decimais exatos:
a) 1,5
b) 4,321
c) 9,83
a) 5,011111…
b) 8,14141414…
c) 0,33333…
Em resumo, todos os números que podem ser representados como uma fração fazem parte do conjunto dos números racionais.
Veja também: Diagrama de Venn — método de representação geométrica dos conjuntos numéricos
Operações com números irracionais
-
Adição e subtração de números irracionais
Para somar ou subtrair números irracionais, o mais comum é usar uma aproximação racional desses números para conseguir realizar as operações. Muitas vezes, ao realizar a soma de dois números racionais, por exemplo, deixamos a operação indicada, mas não realizamos o cálculo em si.
Exemplos:
-
√2 +√3
-
√2 – √3
-
0,0123543… + 4,151492304…
-
Multiplicação e divisão
A multiplicação ou a divisão quando o número é uma raiz não exata é uma operação possível, e o resultado nem sempre é um número irracional.
Exemplos:
-
√50 : √2 =√25 = 5 → Sabemos que 5 é um número racional.
-
√5 · √3 = √15 → Nesse caso, √15 é um número irracional, pois não possui raiz exata.
Exercícios resolvidos
Questão 1 - Durante a resolução de um problema envolvendo o teorema de Pitágoras, Marcelo encontrou o valor √20. Ao tentar calcular essa raiz quadrada, sobre o resultado encontrado, ele escreveu três afirmações.
I. O resultado é um número irracional.
II. A representação decimal é uma dízima periódica.
III. A representação decimal desse número está entre 4 e 5.
Das afirmativas feitas por Marcelo, ele acertou:
A) somente I e II.
B) somente II e III.
C) somente I e III.
D) todas as afirmativas.
E) somente a II.
Resolução
Alternativa C.
I → Correta, pois é uma raiz não exata.
II → Errada, pois uma raiz não exata é uma dízima não periódica.
III → Correta. √20 não é uma raiz exata, mas está entre √16 = 4 e entre √25 = 5.
Somente as afirmativas I e III estão corretas.
Questão 2 - Analise os números a seguir e classifique-os como racionais ou irracionais.
I) 3,1415
II) π
III) 1,123902123…
IV) √36
São considerados números irracionais:
A) somente I e IV.
B) somente II e III.
C) somente II e IV.
D) somente I e II.
E) somente III e IV.
Resolução
Alternativa B.
I → É um número decimal exato, logo é considerado um número racional.
II → O π é um número irracional, pois sua representação decimal é uma dízima não periódica.
III → Esse número é uma dízima não periódica, logo é um número irracional.
IV → Se calcularmos √36, o resultado é 6, que é um número racional.
São números irracionais somente II e III.