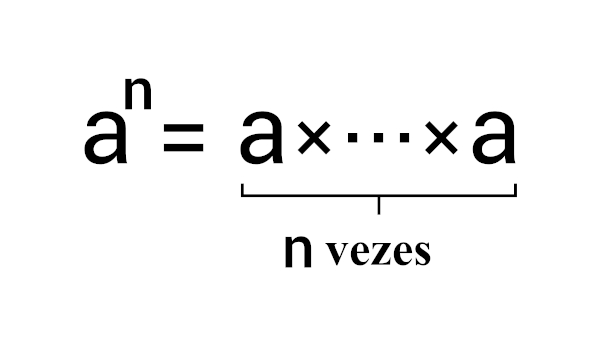A notação científica é uma maneira simplificada de representar os números. Utilizamos a notação científica para representar valores muito grandes ou muito pequenos e para facilitar na realização de operações. Colocar um número em notação científica é escrevê-lo como uma potência de base 10.
Os números que representam valores muito grandes ou valores muito pequenos são frequentemente representados em notação científica como um meio de facilitar tanto a representação quanto a realização de operações com esses números. No estudo da química, da física e da biologia, é bastante comum o uso da notação científica para representar as medidas de algumas grandezas. Um número em notação científica é representado desta forma: k ⸳10n.
Leia também: Técnicas para fazer divisão de números decimais
Tópicos deste artigo
- 1 - Resumo sobre notação científica
- 2 - Videoaula sobre notação científica
- 3 - O que é notação científica?
- 4 - Como colocar um número em notação científica?
- 5 - Operações com números em notação científica
- 6 - Exercícios resolvidos com notação científica
Resumo sobre notação científica
-
Utilizamos a notação científica para representar números muito grandes ou números muito pequenos.
-
Escrever o número em notação científica é representá-lo como uma potência de 10.
-
Um número em notação científica é representado da forma k · 10n.
Videoaula sobre notação científica
O que é notação científica?
Um número em representação científica é escrito sempre em potência de base 10, da seguinte forma:
k ⸳ 10n
Em que k é um número real menor que 10 e n é um expoente inteiro.
Vejamos alguns exemplos:
-
A distância do planeta Terra até Saturno é de 1.673.000.000 de km. Em notação científica, esse número pode ser representado por 1,7 · 109 km.
-
O diâmetro de um átomo mede 0,000.000.000.1 m. Esse número pode ser representado em notação por 1 ·10–10 metros.
Leia também: Propriedades da potenciação — conhecê-las ajuda bastante na notação científica
Como colocar um número em notação científica?
Para a representação de um número em notação científica, é necessário seguir alguns passos:
-
1º passo: deslocar a vírgula do número, de modo que ele se torne um número decimal com apenas um número diferente de zero em sua parte inteira.
-
2º passo: escrever o produto entre o número encontrado anteriormente e uma potência de base 10.
-
3º passo: contar a quantidade de casas que a vírgula deslocou para definir o expoente da potência de base 10.
Observação:
Há dois casos para o expoente: ele pode ser negativo ou positivo.
-
O expoente será positivo se o número representava uma quantidade muito grande e a vírgula foi deslocada da direita para a esquerda, diminuindo o valor do número.
-
O expoente será negativo se o número representava uma quantidade muito pequena e a vírgula foi deslocada da esquerda para direita.
Exemplo 1:
5.420.000.000 m
Quando a vírgula não aparece, ela está no final do número, logo, ela será deslocada da direita para a esquerda, diminuindo o número. Então, nesse caso, em notação científica, colocaremos a vírgula entre 5 e 4, e deslocaremos 9 casas. Assim, esse número em notação científica será:
5,42 · 109 m
Exemplo 2:
0,000.000.000.000.000.000.012 kg
Nesse caso, a vírgula vai ser deslocada da esquerda para a direita, diminuindo o número, e ficará entre 1 e 2, deslocando 20 casas. Como o deslocamento foi da esquerda para a direita, então o expoente será negativo, assim, a representação desse número em notação científica será:
1,2 · 10-20 kg
Operações com números em notação científica
Podemos realizar as quatro operações básicas entre números em notação científica.
-
Soma e subtração com números em notação científica
Para realizar a soma ou a subtração entre dois números em notação científica, é necessário que as potências possuam os mesmos expoentes. Quando os expoentes forem iguais, realizamos as operações entre os números decimais e conservamos a potência. Exemplos:
4,5 · 107 + 3,2 · 10 7 = 7,7 · 107
9,8 · 10³ – 7,4 · 10³ = 2,4 · 10³
-
Multiplicação com números em notação científica
Para realizar a multiplicação entre dois números em notação científica, multiplicamos os números, repetimos a base 10 e somamos os expoentes. Exemplo:
2,3 · 106 × 1,4 · 105 = (2,3 · 1,4) · 105+6 = 3,22 · 1011
-
Divisão com números em notação científica
Ao realizar a divisão de dois números em notação científica, dividimos os números, repetimos a base 10 e subtraímos os expoentes. Exemplo:
8,4 · 108 : 3,5 · 106 = (8,4 : 3,5) ·108-6 = 2,4 · 102
Leia também: Sistema de numeração decimal — o modo como fazemos a representação dos números
Exercícios resolvidos com notação científica
Questão 1
(Enem – 2019) Um asteroide batizado de 2013-TV135 passou a aproximadamente 6,7 × 106 quilômetros da Terra. A presença do objeto espacial nas proximidades da Terra foi detectada por astrônomos ucranianos, que alertaram para uma possível volta do asteroide em 2032.
Disponível em: www1.folha.uol.com.br. Acesso em: 30 out. 2013.
O valor posicional do algarismo 7, presente na notação científica da distância, em quilômetro, entre o asteroide e a Terra, corresponde a
A) 7 décimos de quilômetro.
B) 7 centenas de quilômetros.
C) 7 dezenas de milhar de quilômetros.
D) 7 centenas de milhar de quilômetros.
E) 7 unidades de milhão de quilômetros
Resolução:
Alternativa D
6,7 × 106 = 6.700.000
Então o 7 corresponde à centena de milhar.
Questão 2
(Enem) A Agência Espacial Norte Americana (NASA) informou que o asteroide YU 55 cruzou o espaço entre a Terra e a Lua no mês de novembro de 2011. A ilustração a seguir sugere que o asteroide percorreu sua trajetória no mesmo plano que contém a órbita descrita pela Lua em torno da Terra. Na figura, está indicada a proximidade do asteroide em relação à Terra, ou seja, a menor distância que ele passou da superfície terrestre.
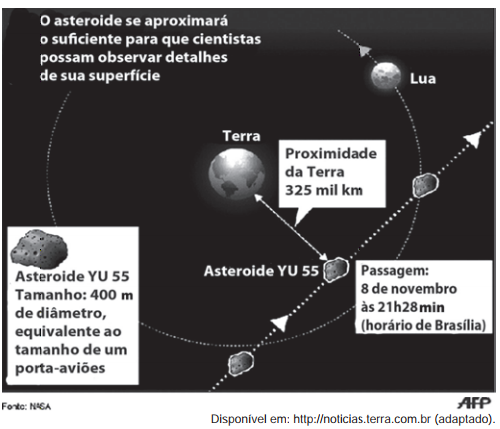
Com base nessas informações, a menor distância que o asteroide YU 55 passou da superfície da Terra é igual a:
A) 3,25 × 102 km
B) 3,25 × 103 km
C) 3,25 × 104 km
D) 3,25 × 105 km
E) 3,25 × 106 km
Resolução:
Alternativa D
Queremos representar 325 mil em notação científica:
325000
Ao colocar a vírgula entre 3 e 2, teremos 5 números após ela. Então, esse número em notação científica será 3,25 × 105 km.