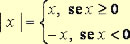Norma de um vetor

Para calcular a norma, ou módulo, de um vetor, é importante ter em mente algumas definições importantes.

Vetores são objetos, geralmente definidos na Geometria Analítica, responsáveis pela orientação de um movimento, isto é, por meio de um vetor, é possível indicar o sentido, a direção e a intensidade de um objeto em movimento.

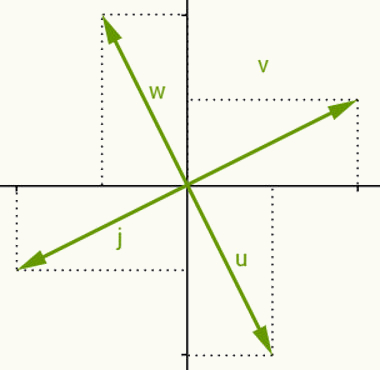
Geralmente os vetores são representados por flechas e são descritos por meio de seus pontos final e inicial. Um vetor v, por exemplo, tem coordenadas a e b. Para descrevê-lo, escreve-se v = (a,b), quando seu ponto inicial é a origem (0,0) e o seu ponto final é o ponto A (a,b).

Exemplo de vetor no plano

Um vetor v no espaço de três dimensões, por sua vez, possui três coordenadas. Escreve-se: v = (a,b,c). No espaço de quatro dimensões, o vetor possui quatro coordenadas e v = (a,b,c,d) e assim por diante.

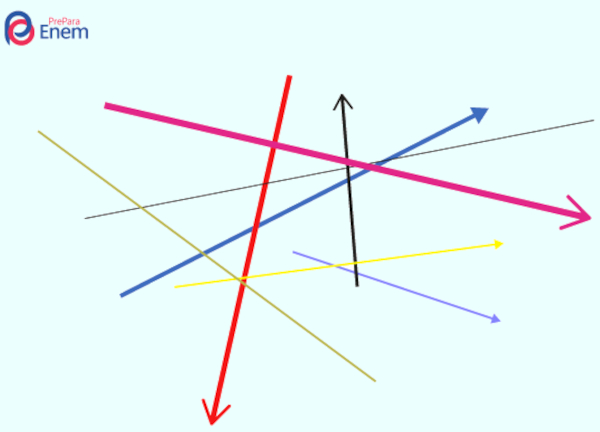
Módulo de um número real

O módulo de um número real é calculado pela distância desse número até a origem. Vale lembrar que a reta numérica, além de constituir um espaço unidimensional, contém todos os números reais. Por esse motivo, podemos utilizá-la como espaço para esses cálculos.

Dado o número real a, a distância de a até zero é o módulo do número real a:

|a| = d(a,0)

Observe o exemplo abaixo, em que fica claro que |10| = |–10| = 10, pois as distâncias de A até a origem C e de B até a origem C são iguais a 10.

Módulo ou norma de um vetor

A ideia de módulo de um número real é a mesma para definir a norma de um vetor. Considerando u = (a,b) como o vetor que parte da origem e finda nas coordenadas (a,b), a norma ou módulo desse vetor é a distância entre o ponto (a,b) e a origem (0,0). Em outras palavras, calcular a norma do vetor v resulta em calcular seu comprimento.

Como esse vetor possui apenas duas coordenadas e, portanto, pertence ao plano bidimensional, utiliza-se a distância entre dois pontos do plano para calcular seu comprimento. Dessa maneira, a norma do vetor u = (a,b) é dada por:

|u| = √(a² + b²)

A norma de um vetor – também conhecida como módulo de um vetor –, portanto, é um número real ligado ao comprimento desse vetor.

Exemplo: Calcule a norma do vetor v = (-9,12)

|v| = √(a² + b²)

|v| = √((-9)² + 12²)

|v| = √(81 + 144)

|v| = √225

|v| = 15