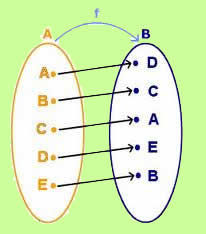
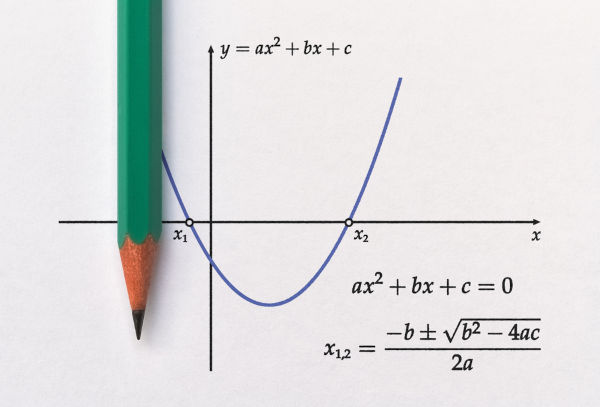
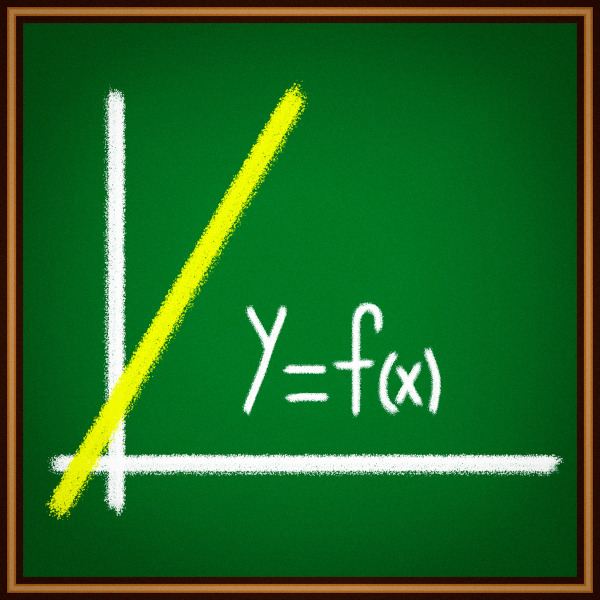
Podemos definir função como uma relação entre duas ou mais grandezas. Veja a seguinte situação:
Exemplo 1
O preço do litro da gasolina em um posto é R$ 2,50.
|
Litros |
Valor a pagar |
|
1 |
R$ 2,50 |
|
2 |
R$ 5,00 |
|
3 |
R$ 7,50 |
|
4 |
R$ 10,00 |
|
5 |
R$ 12,50 |
|
10 |
R$ 25,00 |
|
15 |
R$ 37,50 |
|
20 |
R$ 50,00 |
|
........... |
............... |
O total a pagar depende da quantidade de gasolina abastecida. Podemos estabelecer uma relação entre a quantidade de litros de gasolina e o valor a ser pago:
f(x): preço a pagar (varia de acordo com a quantidade de litros abastecidos)
x: litros (variável)
y: preço do litro (valor pré-fixado)
Temos que a lei de formação da função é: f(x) = 2,50x
Exemplo 2
Um taxista cobra um valor fixo de R$ 4,20 mais R$ 0,30 por quilômetro rodado. Escreva a função que determina o valor de uma corrida e qual o valor que uma pessoa irá pagar por ter usado os serviços do taxista após rodar 20 km.
Função: f(x) = 0,30x + 4,20 (onde x: km rodados e R$ 4,20 valor fixo)
f(x) = 0,30x + 4,20
f(20) = 0,30 * 20 + 4,20
f(20) = 6 + 4,20
f(20) = 10,20
A pessoa irá pagar R$ 10,20 pelo serviço prestado.
Exemplo 3
Carlos é um técnico em eletrônica e presta serviços autônomos. Por uma visita ele cobra R$ 40,00 mais R$ 5,00 por hora de trabalho. Quanto Carlos irá cobrar por um trabalho que demorou 9 horas?
Função: f(x) = 5x + 40
f(x) = 5x + 40
f(9) = 5 * 9 + 40
f(9) = 45 + 40
f(9) = 85
Carlos irá cobrar R$ 85,00.
Exemplo 4
Para produzir um determinado produto, uma indústria tem um custo fixo de R$ 32,00 mais R$ 1,50 por peça produzida. Qual o custo de produção de 500 peças?
Função: f(x) = 1,5x + 32
f(500) = 1,5 * 500 + 32
f(500) = 750 + 32
f(500) = 782
O custo para a produção de 500 peças será de R$ 782,00.