A divisão de frações é uma operação matemática. Essa operação determina que a divisão entre duas frações é igual à multiplicação entre a primeira fração pelo inverso da segunda fração.
Leia também: Adição e subtração de frações
Resumo sobre divisão de frações
-
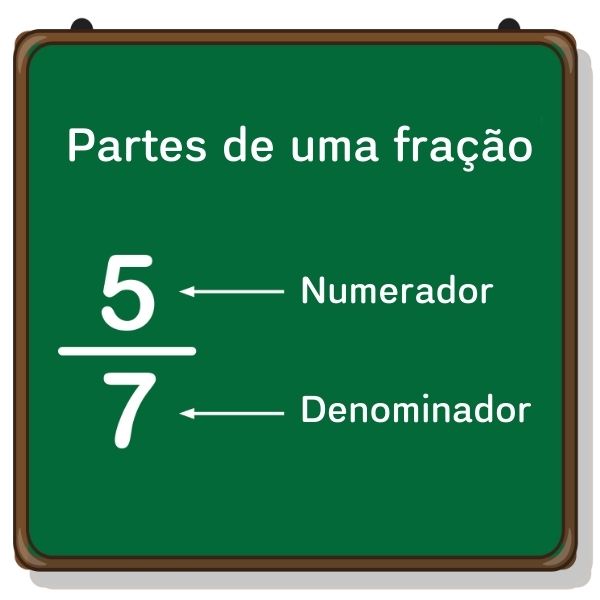
Divisão de frações é uma operação matemática.
-
A divisão entre as frações \(\frac{a}b\) e \(\frac{c}d\) é igual à multiplicação entre as frações \(\frac{a}b\) e \(\frac{d}c\).
-
Podemos representar a divisão entre as frações \(\frac{a}b\) e \(\frac{c}d\) das seguintes maneiras: \(\frac{a}{b}÷\frac{c}{d}=a/b÷c/d=\frac{\frac{a}{b}}{\frac{c}{d}}\)
Como se faz a divisão de frações?
Considere as frações \(\frac{a}b\) e \(\frac{c}d\), em que a, b, c e d representam números quaisquer, com \(b≠0\ e\ d≠0\). Assim, a divisão de \(\frac{a}b\) e \(\frac{c}d\) é a multiplicação de \(\frac{a}b\) e \(\frac{d}c\) . Em notação matemática:
\(\frac{a}b÷\frac{c}d=\frac{a}b×\frac{d}c=\frac{ad}{bc}\)
Em outras palavras, a divisão de duas frações é calculada pela multiplicação da primeira fração pelo inverso da segunda (ou seja, trocando o numerador pelo denominador e vice-versa). Vejamos um exemplo.
Exemplo 1: Calcule a divisão \(\frac{2}{3}÷\frac{1}4\).
A divisão de \(\frac{2}3\) por \(\frac{1}4\) é a multiplicação de \(\frac{2}3\) por \(\frac{4}1\):
\(\frac{2}3÷\frac{1}4=\frac{2}3×\frac{4}1=\frac{2‧ 4}{3‧1}=\frac{8}3 \)
Observação: A operação de divisão de frações ocorre da mesma maneira para frações com denominadores iguais ou diferentes. Isso significa que o procedimento para resolver uma operação de divisão de frações é único.
Exemplo 2: Calcule a divisão \(\frac{1}2÷\frac{5}2\).
A divisão de \(\frac{1}2\) por \(\frac{5}2\) é a multiplicação de \(\frac{1}2\) por \(\frac{2}5\):
\(\frac{1}2÷\frac{5}2=\frac{1}2×\frac{2}5=\frac{1‧2}{2‧5}=\frac{2}{10}=\frac{1}5\)
Representação da divisão de frações
Até aqui, representamos a divisão das frações \(\frac{a}b\) e \(\frac{c}d\) pela notação \(\frac{a}{b}÷\frac{c}d\). No entanto, há outras maneiras de escrever essa operação, como identificando a barra da fração pelo símbolo /, escrevendo \(a/b÷c/d\).
Uma terceira possibilidade é considerar que a barra de fração simboliza uma divisão, e, portanto, uma fração pode ser utilizada para expressar a divisão entre duas frações. Parece confuso, mas é apenas uma questão de escrita. Observe a representação a seguir:
\(\frac{\frac{a}{b}}{\frac{c}{d}}\)
Perceba que é possível visualizar essa composição como uma fração de numerador \(\frac{a}b\) e denominador \(\frac{c}d\). Portanto, isso se refere à divisão \(\frac{ a}b÷\frac{c}d\).
Em resumo, as representações são:
\(\frac{a}{b}÷\frac{c}{d}=a/b÷c/d=\frac{\frac{a}{b}}{\frac{c}{d}}\)
No exemplo anterior, calculamos a divisão \(\frac{1}2÷\frac{5}2\). Essa operação pode ser expressa por:
\(\frac{\frac{1}{2}}{\frac{5}{2}}\)
Leia também: Como fazer a simplificação de frações?
Exercícios resolvidos sobre divisão de frações
Questão 1
Qual o resultado da operação \(\frac{3}2÷\frac{1}7 \)?
A) 3,7
B) 9,1
C) 2,3
D) 10,5
E) 8,7
Solução
Alternativa D
A divisão de \(\frac{3}2\) por \(\frac{1}7\) é calculada pela multiplicação entre \(\frac{3}2\) por \(\frac{7}1\):
\(\frac{3}2÷\frac{1}7=\frac{3}2×\frac{7}1=\frac{3‧7}{2‧1}=\frac{21}2\)
Como as alternativas estão em formato decimal, devemos converter o resultado \(\frac{21}2\) em notação decimal: \(\frac{ 21}2=10,5\).
Questão 2
Considere \( A=\frac{7}9÷\frac{2}3\) e \(B=\frac{1}5÷\frac{1}6\). Qual o valor de A/B?
Solução
Primeiramente, vamos determinar o valor de A:
\(A=\frac{7}9÷\frac{2}3=\frac{7}9×\frac{3}2=\frac{7‧3}{9‧2}=\frac{21}{18}=\frac{7}6\)
Agora, determinamos o valor de B:
\(B=\frac{1}5÷\frac{1}6=\frac{1}5×\frac{6}1=\frac{1‧6}{5‧1}=\frac{6}5\)
Assim, A/B é a divisão de \(\frac{7}6\) por \(\frac{6}5\):
\(A/B=\frac{7}6÷\frac{6}5=\frac{7}6×\frac{5}6=\frac{35}{36} \)
