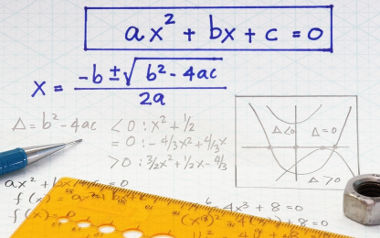O método de completar quadrados é uma alternativa que pode ser usada para encontrar soluções de equações do segundo grau em sua forma normal (ou reduzida). Dependendo da prática, é possível calcular os resultados de algumas equações apenas com cálculo mental a partir desse método. Para tanto, é importante saber o que são produtos notáveis, a forma como as equações do segundo grau podem ser escritas e a relação que existe entre esses dois fatores.
Relação entre equações do segundo grau e produtos notáveis
As equações do segundo grau, na forma normal, são escritas da seguinte maneira:
ax2 + bx + c = 0
Essa forma em muito se parece com o trinômio quadrado perfeito, que é resultado de um dos produtos notáveis: quadrado da soma ou quadrado da diferença. Observe o primeiro deles:
(y + k)2 = y2 + 2xk + k2
Note que, se a = 1, b = 2k e c = k2, podemos escrever:
(y + k)2 = y2 + 2xk + k2 = ax2 + bx + c
Dessa maneira, é possível resolver equações do segundo grau comparando os termos de sua forma reduzida com um produto notável e, assim, evitar o método resolutivo de Bhaskara. Isso será feito em dois casos: no primeiro, a equação do segundo grau é um trinômio quadrado perfeito e resultado direto de um produto notável; no segundo, as equações do segundo grau não são.
Primeiro caso: O trinômio quadrado perfeito
Quando uma equação do segundo grau é um trinômio quadrado perfeito, é possível escrevê-la na forma fatorada, ou seja, retornar ao produto notável que a originou. Veja esta equação:
x2 + 8x + 16 = 0
Trata-se de um trinômio quadrado perfeito. O método para provar isso pode ser encontrado clicando aqui. Em resumo, o termo do meio é igual a duas vezes a raiz do primeiro termo vezes a raiz do segundo termo. Quando isso não acontece, a expressão observada não é fruto de um produto notável.
Resolver essa equação pode ser fácil quando se sabe que o produto notável que gerou essa equação é:
(x + 4)2 = x2 + 8x + 16 = 0
Logo, podemos escrever:
(x + 4)2 = 0
O próximo passo é calcular a raiz quadrada dos dois lados da equação. Observe que o lado esquerdo resultará na própria base da potência por causa das propriedades dos radicais. Já o lado direito continuará sendo zero, pois a raiz de zero é zero.
√[(x + 4)2] = √0
x + 4 = 0
Agora, basta finalizar utilizando conhecimentos sobre equações:
X + 4 = 0
x = – 4
As equações do segundo grau podem ter de zero a dois resultados dentro do conjunto dos números reais. A equação acima possui apenas 1. Na realidade, todas as equações que são trinômios quadrados perfeitos possuem apenas um resultado real.
Segundo caso: a equação do segundo grau não é trinômio quadrado perfeito
Quando a equação não for trinômio quadrado perfeito, é possível resolvê-la usando o mesmo princípio. Só é necessário realizar um pequeno procedimento antes. Observe o exemplo:
x2 + 8x – 48 = 0
Para que essa equação seja trinômio quadrado perfeito, o seu último termo deve ser + 16, e não o – 48. Se esse número estivesse no lado esquerdo da equação, poderíamos escrevê-la como um produto notável e resolvê-la de modo parecido com o que foi feito no exemplo anterior. O procedimento a ser realizado nesse caso é justamente para que esse + 16 apareça e o – 48 suma.
Para isso, apenas some 16 nos dois lados da equação. Isso não mudará seu resultado final, pois essa é uma das propriedades das equações.
x2 + 8x – 48 + 16 = 0 + 16
Para que seja possível transformar a equação em trinômio quadrado perfeito, basta tirar o – 48 do lado esquerdo. O método para fazer isso também é uma das propriedades das equações. Observe:
x2 + 8x – 48 + 16 = 0 + 16
x2 + 8x + 16 = 16 + 48
x2 + 8x + 16 = 64
Agora escreva o lado esquerdo como trinômio quadrado perfeito e calcule a raiz quadrada em ambos os lados.
x2 + 8x + 16 = 64
(x + 4)2 = 64
√[(x + 4)2] = √64
Observe que, dessa vez, o lado direito da igualdade não é zero, portanto, teremos um resultado não nulo. Em equações, os resultados de raízes quadradas podem ser negativos ou positivos. Por isso, usamos o símbolo ± da seguinte maneira:
x + 4 = ± 8
Isso significa que essa equação deve ser resolvida uma vez para 8 positivo e outra para 8 negativo.
X + 4 = 8
x = 8 – 4
x = 4
ou
x + 4 = – 8
x = – 8 – 4
x = – 12
Logo, as raízes da equação x2 + 8x – 48 = 0 são: 4 e – 12.