Mediatriz

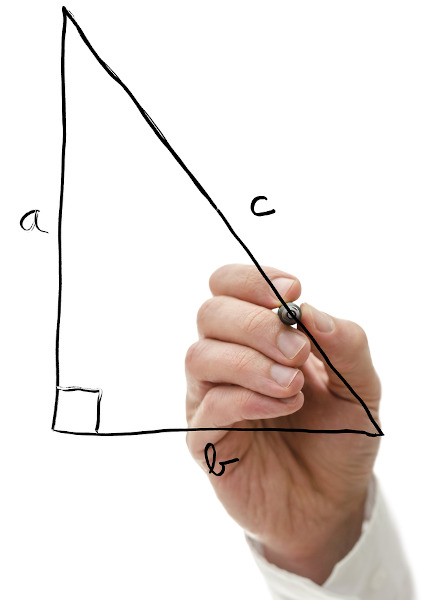
A mediatriz de um segmento é a reta perpendicular ao segmento que cruza o ponto médio. Uma propriedade importante da mediatriz é que cada um de seus pontos está à mesma distância das extremidades do segmento.

Leia também: Como determinar o ponto médio de um segmento no plano?

Tópicos deste artigo

• 1 - Resumo sobre mediatriz
• 2 - O que é mediatriz?
• 3 - Como se constrói a mediatriz?
• 4 - Como se calcula a equação da mediatriz?
• 5 - Mediatriz de um triângulo
• 6 - Quais são as diferenças entre mediatriz, mediana, bissetriz e altura de um triângulo?
• 7 - Exercícios resolvidos sobre mediatriz

Resumo sobre mediatriz

• A reta perpendicular a um segmento que intercepta seu ponto médio é chamada de mediatriz do segmento.

• Utilizando régua e compasso é possível construir a mediatriz de um segmento.

• A equação de uma mediatriz está associada às coordenadas das extremidades do segmento.

• A mediatriz de um triângulo é a reta perpendicular a um dos lados que cruzam o ponto médio.

• O ponto de encontro das mediatrizes de um triângulo é chamado de circuncentro.

• A mediatriz de um triângulo não pode ser confundida com a mediana, a bissetriz ou a altura do triângulo.

• A mediana de um triângulo é o segmento que une um vértice com o ponto médio do lado oposto.

• A bissetriz de um triângulo é o segmento que divide ao meio um dos ângulos internos.

• A altura de um triângulo é o segmento perpendicular a um dos lados com extremidade no vértice oposto.

O que é mediatriz?

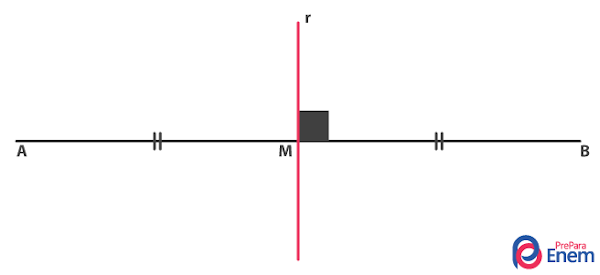
Dado um segmento AB de ponto médio M, a mediatriz é a reta perpendicular a AB que contém M. Na imagem abaixo, r é a mediatriz de AB. 

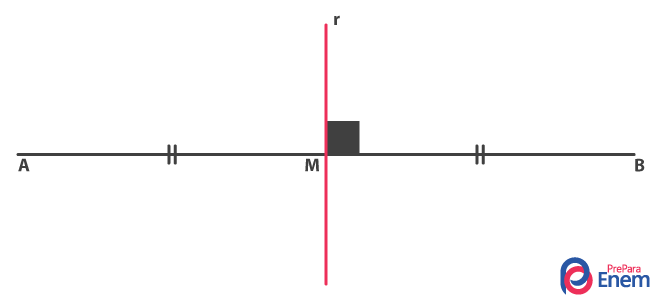
Cada ponto da mediatriz r é equidistante de A e B. Isso significa que se P é um ponto de r, então \(PA = PB\).

Como se constrói a mediatriz?

Para construir a mediatriz de um segmento, utilizamos régua e compasso. Considere o segmento abaixo.

A construção da mediatriz desse segmento deve seguir 3 passos.

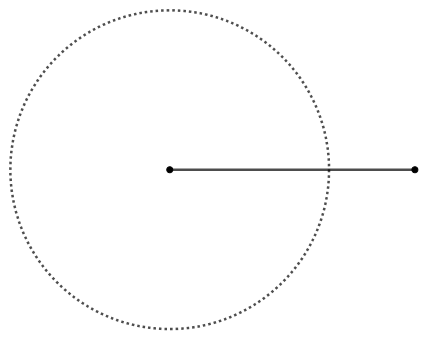
• Passo 1: Abra o compasso em uma medida maior que metade do segmento. Posicione a ponta seca do compasso em uma das extremidades do segmento e desenhe uma circunferência.

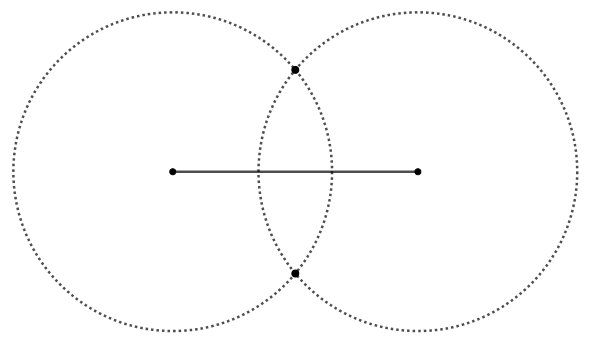
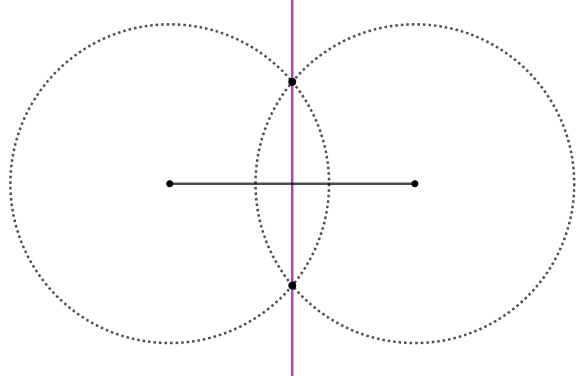
• Passo 2: Repita o passo anterior na outra extremidade do segmento. Observe que as circunferências se interseccionam em dois pontos.

• Passo 3: Com uma régua, construa a reta que contém os dois pontos em comum das circunferências. Essa reta, representada em roxo na imagem a seguir, é a mediatriz do segmento original.

Como se calcula a equação da mediatriz?

A equação da mediatriz é a equação de uma reta. Assim, uma possibilidade é utilizar a equação fundamental da reta

\(y-y_0=m(x-x_0 )\)

• \((x_0,y_0 )\) → um dos pontos da mediatriz e m é seu coeficiente angular.

Exemplo:

Qual a equação da mediatriz do segmento formado por \(A=(2,2)\) e \(B=(4,1)\)?

Resolução:

Procuramos a equação da reta perpendicular a AB que contém o ponto médio de AB. Isso significa que podemos utilizar as coordenadas \((x_0,y_0 )\) desse ponto médio na expressão da equação fundamental da reta.

Considere \(M =(x_0,y_0 )\) o ponto médio de AB. Assim,

\(x_0=\frac{x_A+x_B}2=\frac{2+4}2=3\)

\(y_0=\frac{y_A+y_B}2=\frac{2+1}2=1,5\)

Logo, \(M =(3 ,1,5)\).

Para aplicar a equação fundamental da reta, ainda precisamos descobrir o coeficiente angular da mediatriz.

Considere r a mediatriz de AB e s a reta que contém o segmento AB. Como as retas r e s são perpendiculares, então seus coeficientes angulares \(m_r\) e \(m_s\) se relacionam da seguinte maneira:

\(m_r=-\frac{1}{m_s }\)

Como \(A=(2,2)\) e \(B=(4,1)\) são pontos de s, temos que

\(m_s=\frac{Δy}{Δx}=\frac{(1-2)}{(4-2)}=\frac{-1}2\)

Portanto, o coeficiente da reta r (ou seja, da mediatriz de AB) é

\(m_r=-\frac{1}{\frac{-1}{2}}=2\)

Por fim, utilizamos a equação fundamental da reta para encontrar a equação da mediatriz:

\(y-y_0=m(x-x_0 )\)

\(y-1,5=2(x-3)\)

\(y = 2x -4,5\)

Mediatriz de um triângulo

As mediatrizes de um triângulo (polígono que possui três lados e três ângulos) são as mediatrizes de cada um dos lados, ou seja, as retas perpendiculares aos lados que cruzam os pontos médios.

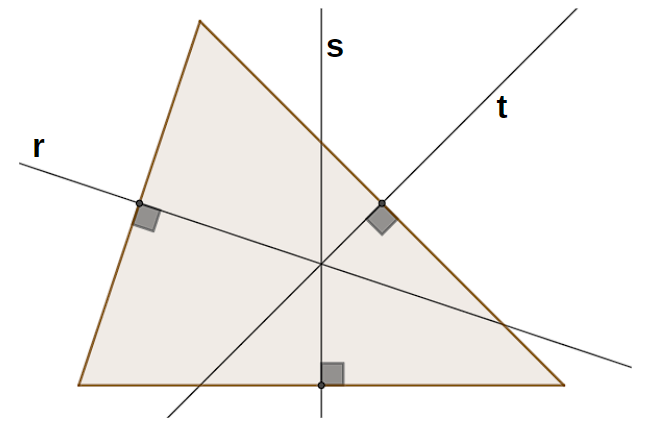
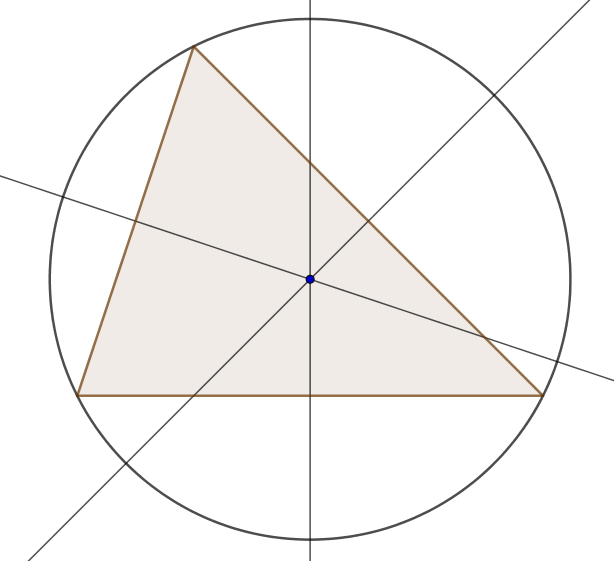
O ponto de encontro das mediatrizes é conhecido como circuncentro. Esse ponto é o centro da circunferência circunscrita ao triângulo.

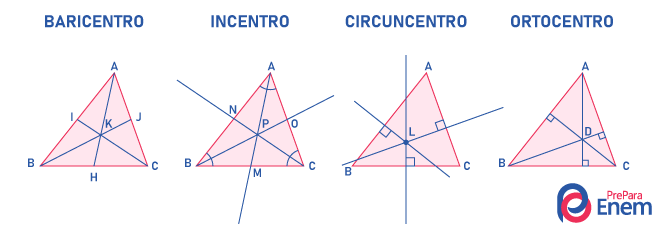
Quais são as diferenças entre mediatriz, mediana, bissetriz e altura de um triângulo?

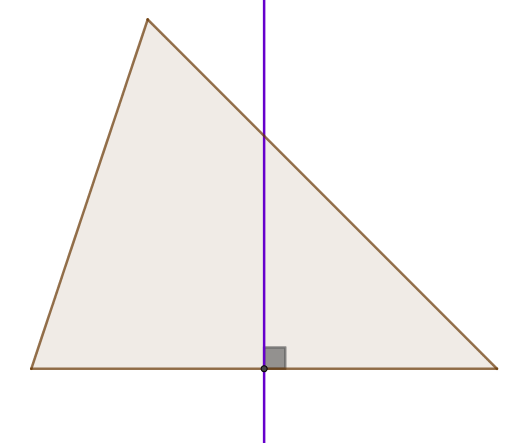
• Mediatriz de um triângulo: é a reta perpendicular a um dos lados que cruza o ponto médio.

• Mediana de um triângulo: é o segmento que une um vértice com o ponto médio do lado oposto.

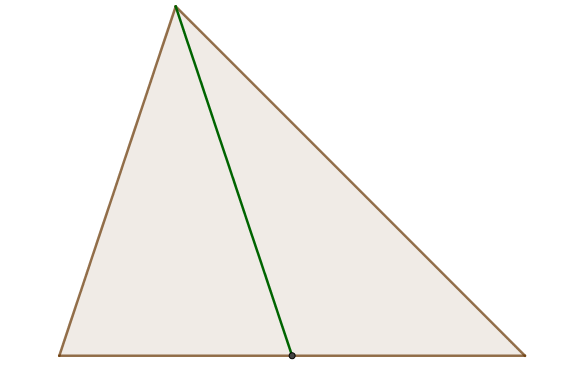
• Bissetriz de um triângulo: é o segmento que divide um dos ângulos internos em ângulos congruentes.

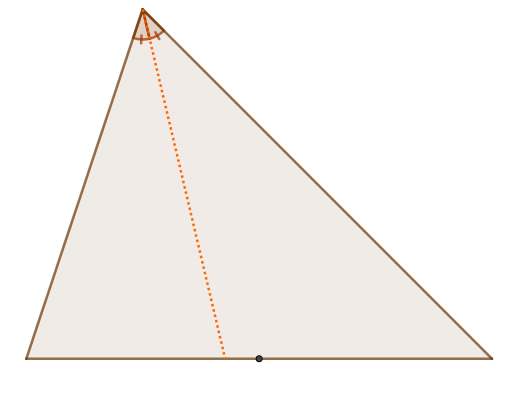
• Altura de um triângulo: é o segmento perpendicular a um dos lados com extremidade no vértice oposto.

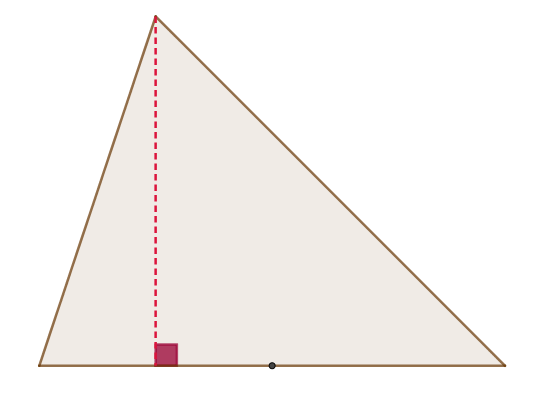
Veja também: O que o teorema da bissetriz interna demonstra?

Exercícios resolvidos sobre mediatriz

Questão 1

Classifique as afirmações abaixo em V (verdadeira) ou F (falsa).

I. Se r é a mediatriz do segmento AB, então r contém os pontos A e B.

II. O ponto de encontro das mediatrizes de um triângulo é o centro da circunferência inscrita no triângulo.

III. A mediatriz de um triângulo divide um dos ângulos em dois ângulos de mesma medida.

A ordem correta, de cima para baixo, é

A) V-V-V

B) V-F-V

C) F-V-F

D) F-F-V

E) F-F-F

Resolução:

Alternativa E.

I. Se r é a mediatriz do segmento AB, então r contém os pontos A e B. (falsa)

Se r é a mediatriz do segmento AB, então r contém o ponto médio de A e B, mas não os pontos A e B.

II. O ponto de encontro das mediatrizes de um triângulo é o centro da circunferência inscrita no triângulo. (falsa)

O ponto de encontro das mediatrizes de um triângulo é o circuncentro do triângulo, ou seja, o centro da circunferência circunscrita ao triângulo.

III. A mediatriz de um triângulo divide um dos ângulos em dois ângulos de mesma medida. (falsa)

Essa é a definição da bissetriz de um triângulo.

Questão 2

(Unicamp) No plano cartesiano, considere a reta de equação x + 2y = 4, sendo A, B os pontos de interseção dessa reta com os eixos coordenados. A equação da reta mediatriz do segmento de reta AB é dada por

A) 2x – y = 3.

B) 2x – y = 5.

C) 2x + y = 3.

D) 2x + y = 5.

Resolução:

Alternativa A.

Considere r a equação dada. Note que \(x+2y=4⇒y=-\frac{1}2 x+2\). Ou seja, \(m_r=-\frac{1}2\) é o coeficiente angular de r.

Perceba que r intercepta os eixos coordenados nos pontos em que x = 0 e y = 0, ou seja

\(A=(0,2)\ e\ B=(4,0)\)

O ponto médio M de AB é

\(M=(\frac{0+4}{2},\frac{2+0}{2})=(2,1)\)

Considere s a mediatriz de AB. Assim, s cruza o ponto M = (2,1) e possui o seguinte coeficiente angular:

\(m_s=-\frac{1}{m_r} =2\)

Utilizando a equação fundamental da reta, temos que a equação de s é

\(y-y_0=m(x-x_0 )\)

\(y-1=2(x-2)\)

\(2x - y =3\)