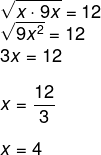Média geométrica

Na estatística, não só a média geométrica, mas todas as médias são essenciais para buscar um único valor que melhor represente os resultados obtidos em um conjunto de dados. São conhecidas como médias pitagóricas a média geométrica, a média aritmética e a média harmônica. O conjunto de dados e a forma como seus elementos se relacionam indicam qual deve ser a melhor média a ser aplicada.

A média geométrica é aplicada em dados que se comportam como uma progressão geométrica, cujo crescimento é próximo ao de uma função exponencial. Para encontrar o valor dela, utilizamos uma fórmula específica. Dado um conjunto com n elementos, a média geométrica é dada pela raiz enésima do produto desses elementos.

Leia também: Estatística no Enem: como esse tema é cobrado?

Tópicos deste artigo

• 1 - Fórmula da média geométrica
• 2 - Como se calcula a média geométrica
• 3 - Aplicações da média geométrica
  • → Aplicação na geometria
• 4 - → Aplicação em progressão geométrica
• 5 - Diferença entre média geométrica e média aritmética
• 6 - Exercícios resolvidos

Fórmula da média geométrica

Para encontrar a média geométrica em um conjunto A, sendo A = {x₁, x₂, x₃, ... x_n} um conjunto de valores com n elementos, utilizamos a fórmula:

Como se calcula a média geométrica

Basta aplicar a fórmula para encontrar o valor da média geométrica.

Exemplo:

Vamos calcular a média geométrica do conjunto a seguir.

A:{3,9, 12, 24, 32}

Em primeira análise, é possível perceber que esse conjunto possui 5 elementos, logo vamos calcular a raiz 5ª do produto entre esses números.

Para realizar a simplificação, podemos contar com a ajuda de uma calculadora e realizar a multiplicação de todos esses números e, posteriormente, calcular a raiz quinta. Outra forma, que é a que vamos utilizar, é reescrever os números em fatores primos para facilitar a conta.

Realizando a decomposição em fatores primos, temos:

Então:

3 = 3

9 = 3²

12 = 3·2²

24 = 3· 2³

32 = 2⁵

Realizando as substituições na fórmula, teremos:

Agora aplicando a propriedade das potências, podemos somar os expoentes de base igual, logo encontraremos:

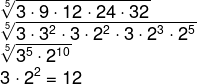
Logo, a média geométrica do conjunto A é igual a 12.

Veja também: Medidas de dispersão: amplitude e desvio

Aplicações da média geométrica

Podemos aplicar a média geométrica em situações cotidianas que envolvam progressões geométricas. Tendo um conjunto de dados, é sempre possível encontrar a média geométrica entre eles.

Exemplo 1

→ Aplicação na geometria

Um quadrado e um retângulo possuem a mesma área. Sabendo que as dimensões do retângulo são 12 e 4, calcule o valor do lado do quadrado.

Como a área é calculada pelo produto entre a base e a altura do retângulo e, nesse caso, elas são iguais, então basta calcular a média geométrica dos lados do retângulo.

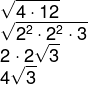
Exemplo 2

→ Aplicação em progressão geométrica

A população de uma determinada cultura de bactérias foi medida diariamente durante 5 dias e pode ser representada pela PG (1,3,9,27,81). Qual é a média geométrica desse conjunto?

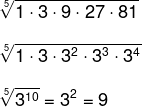
Note que a média geométrica da progressão foi o termo central. Isso sempre vai ocorrer em se tratando de uma progressão geométrica.

Diferença entre média geométrica e média aritmética

A média geométrica e a média aritmética, junto com a média harmônica, são conhecidas como médias pitagóricas. Todas as três são utilizadas na estatística, cada uma delas em um caso. A média aritmética é a mais comum delas, e a diferença entre ela e a média geométrica não está na importância entre elas, mas sim na fórmula utilizada para calculá-las. Como as fórmulas são diferentes, dado um mesmo conjunto de dados, a média aritmética e a média geométrica são quase sempre valores diferentes.

Vejamos as fórmulas para calcular cada uma delas:

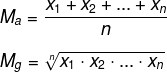
M_a → média aritmética

M_g → média geométrica

n → quantidade de elementos no conjunto

Exemplo:

Dado o conjunto A: (4,6,8,10), calcule a média geométrica e a média aritmética desse conjunto.

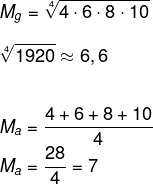
Acesse também: Medidas de estatística: médias aritmética, ponderada e geométrica

Exercícios resolvidos

Questão 1 – Um cubo e um prisma possuem a mesma capacidade. Sabendo que o prisma possui base retangular e que as suas dimensões são 10 cm, 12 cm e 9 cm. Cada uma das arestas do cubo mede:

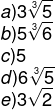
Resolução

Alternativa D.

Como a capacidade dos sólidos é a mesma, então, para encontrar a aresta do cubo, basta calcular a média geométrica entre as arestas do prisma.

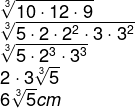
Questão 2 – Em uma progressão geométrica, a média geométrica entre o sucessor e o antecessor de n é sempre igual ao próprio n. Sabendo disso, o valor de x na progressão geométrica (x, 12, 9x) é de?

a) 1

b) 2

c) 3

d) 4

e) 5

Resolução

Alternativa D.

Por ser uma progressão geométrica, sabemos que a média geométrica entre x e 9 x é igual a 12.