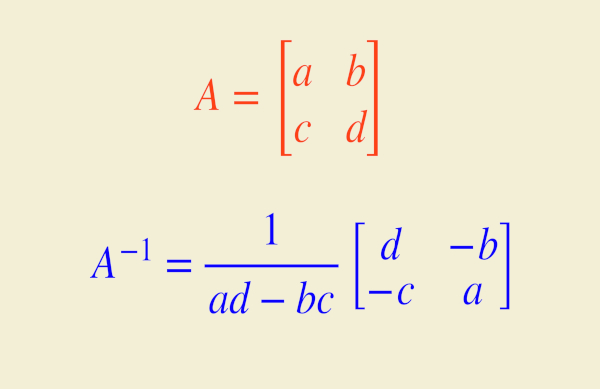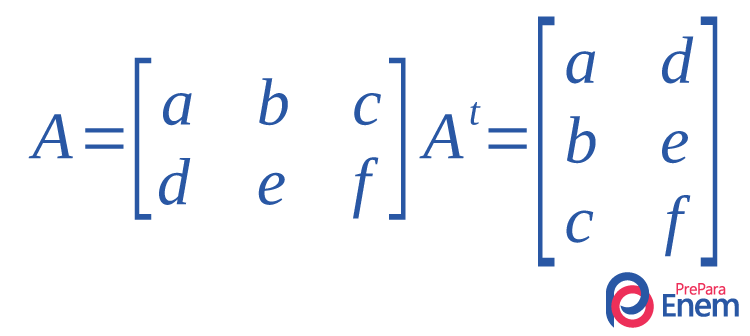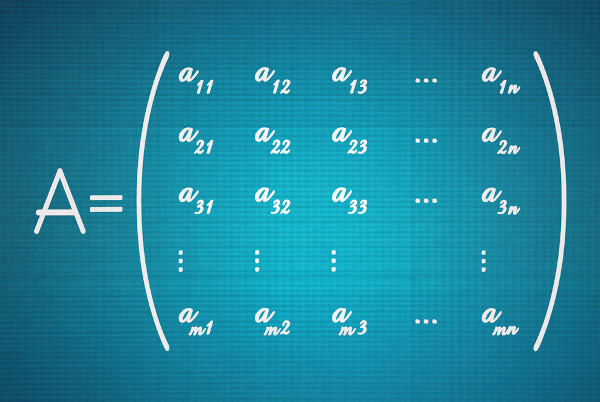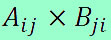No estudo de Matrizes, é importante atentar para a forma como cada elemento é representado. Os elementos de uma matriz A podem ser caracterizados da forma Aij, em que i representa a linha e j representa a coluna onde o elemento se encontra. Por exemplo, um elemento da forma A23 está localizado na segunda linha e na terceira coluna de uma matriz.
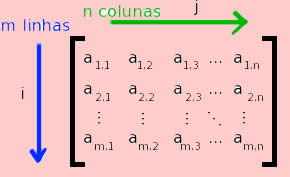
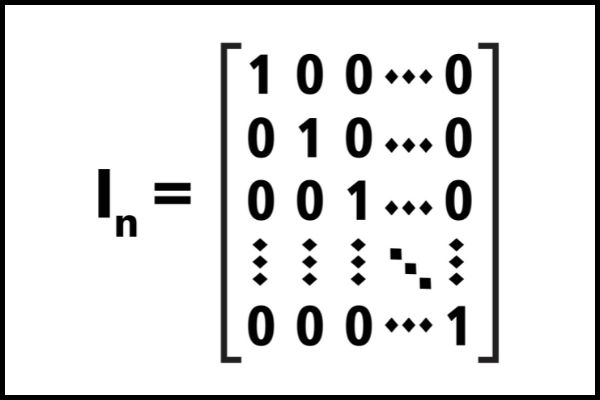
Uma importante matriz é a matriz quadrada, que é caracterizada por ter exatamente o mesmo número de linhas e colunas. Veja a seguir um exemplo:

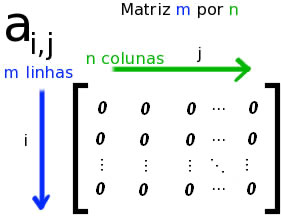
Na imagem, há uma matriz quadrada de ordem nxn. Os elementos em vermelho compõem a diagonal principal da matriz
Os elementos destacados em vermelho na imagem são aqueles que compõem a diagonal principal da matriz. Esses elementos possuem índices i e j iguais, isto é, são da forma A11, A22 e Ann.
Observe que, nos elementos à direita e acima da diagonal principal, o número da linha é inferior ao número da coluna. Quando esses elementos forem todos nulos, teremos uma matriz triangular inferior. Simplificando, podemos dizer que, se Aij = 0, para i < j, há uma matriz triangular inferior. Veja na imagem a seguir como uma matriz triangular inferior caracteriza-se:

Na matriz triangular inferior, todos os elementos à direita e acima da diagonal principal são nulos
Quando ocorrer o contrário, ou seja, quando os elementos à esquerda e abaixo da diagonal principal forem nulos, teremos uma matriz triangular superior, ou, simplesmente, se Aij = 0, para i > j. A seguir temos o exemplo de uma matriz triangular superior genérica:

Na matriz triangular superior, os elementos à esquerda e abaixo da diagonal principal são nulos
Seria possível uma mesma matriz ser simultaneamente triangular superior e triangular inferior? Sim! Se forem nulos todos os elementos que não pertencem à diagonal principal, essa matriz será triangular superior e inferior. Esse tipo de matriz recebe um nome especial, é chamada de matriz diagonal.
E como seria a matriz transposta de uma matriz triangular qualquer? Ao fazer a transposição de uma matriz triangular superior, ela se tornará uma matriz triangular inferior. O contrário também vale, a transposta de uma matriz triangular inferior é uma matriz triangular superior. Vejamos um exemplo:

Ao fazer a transposição de uma matriz triangular superior, ela se transformará em uma triangular inferior. O mesmo vale para uma triangular inferior
Veja outras propriedades importantes sobre matrizes triangulares que podem ajudar bastante:
-
Vale lembrar que toda matriz triangular é quadrada, mas nem toda matriz quadrada é triangular;
-
Ao multiplicar matrizes triangulares inferiores, obtemos também uma matriz triangular inferior. O mesmo vale para matrizes triangulares superiores;
-
A inversa de uma matriz triangular inferior é também uma matriz triangular inferior. O mesmo ocorre com a inversão de uma matriz triangular superior.
-
Só é possível inverter uma matriz triangular se nenhum dos elementos da diagonal principal é zero.
Aproveite para conferir nossa videoaula sobre o assunto: