Matriz transposta

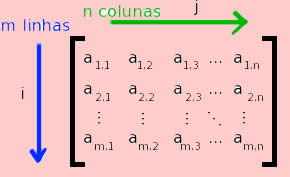
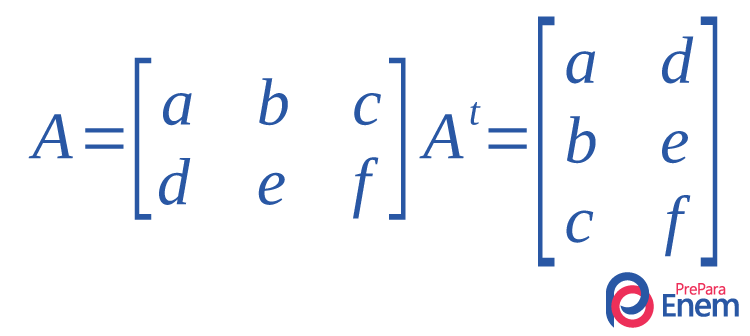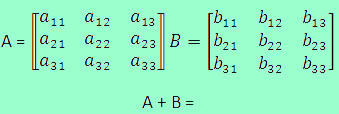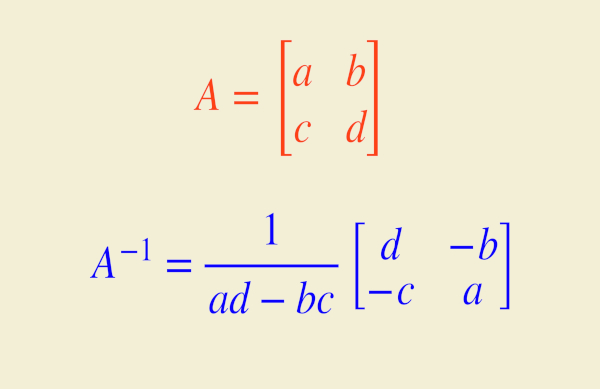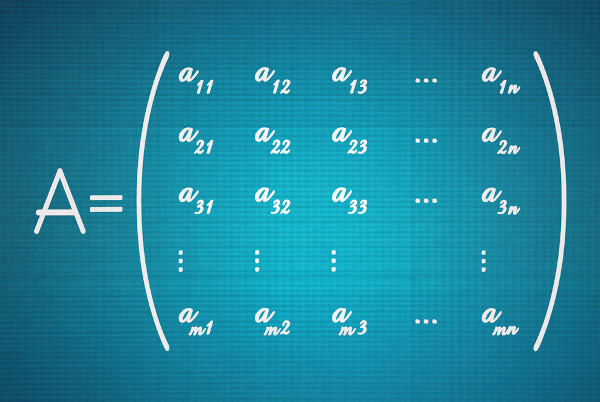A matriz transposta de uma matriz A é uma matriz A^t cujas colunas são as linhas de A e cujas linhas são as colunas de A, na mesma ordem. Formalmente, representamos a transposta da matriz \(\left[a_{ij}\right]_{mxn} \) por \(A^t=\left[a_{ji}\right]_{nxm}\). 

Considere, por exemplo, uma matriz A de ordem 2x3. Assim, a primeira linha de A será a primeira coluna de Ate a segunda linha de A será a segunda coluna de A^t. Note que A^t é de ordem 3x2 e que cada elemento a_ij de A é o elemento aji de A^t.

Leia também: Matriz triangular — a matriz cujos elementos acima ou abaixo da diagonal principal são nulos

Tópicos deste artigo

• 1 - Resumo sobre matriz composta
• 2 - Quais são as propriedades da matriz transposta?
• 3 - Como obter a matriz transposta?
• 4 - O que é matriz simétrica?
• 5 - O que é matriz inversa?
• 6 - O que é matriz oposta?
• 7 - Exercícios resolvidos sobre matriz transposta

Resumo sobre matriz composta

• A matriz transposta de uma matriz A é a matriz representada por A^t.
• As linhas de A são as colunas de A^t, e as colunas de A são as linhas de A^t.
• Existem cinco propriedades principais de uma matriz transposta.
• Para obter a transposta de uma matriz A, devemos transformar as linhas de A em colunas e as colunas de A em linhas.
• Se uma matriz é igual à sua transposta, então é chamada de matriz simétrica.
• Uma matriz M^-1 é inversa de M caso o produto entre M e M^-1 seja a matriz identidade.
• Uma matriz -N é oposta de N se a soma entre N e -N for matriz nula.

Quais são as propriedades da matriz transposta?

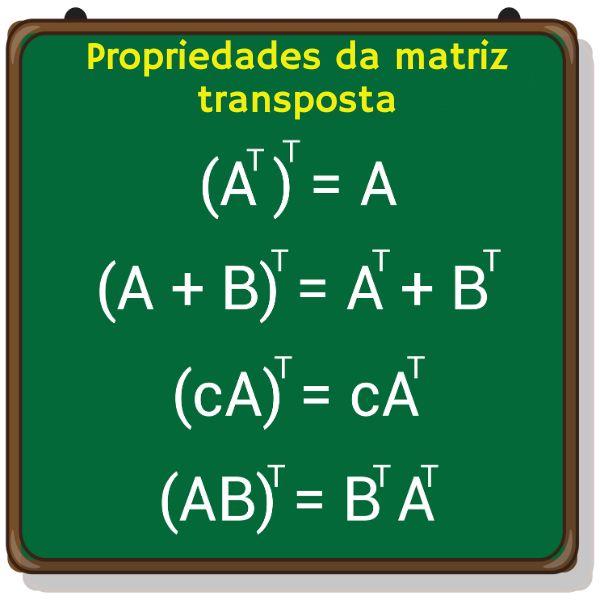
Uma matriz transposta apresenta 5 propriedades principais:

• Propriedade 1: a transposta da transposta é igual à matriz original. Dada uma matriz A, temos que

\(\left(A^t\right)^t=A\)

• Propriedade 2: a transposta da soma é igual à soma das transpostas, na mesma ordem. Considere duas matrizes A e B de mesma ordem. Assim,

\(\left(A+B\right)^t=A^t+B^t\)

• Propriedade 3: a transposta da multiplicação de uma constante por uma matriz é igual à multiplicação da constante pela transposta da matriz. Considere A uma matriz e c uma constante (um número real). Então,

\(\left(cA\right)^t=cA^t\)

• Propriedade 4: a transposta de um produto de matrizes é igual ao produto das transpostas na ordem contrária. Considere duas matrizes A e B tais que o produto AB seja possível. Assim,

\(\left(AB\right)^t=B^tA^t\)

• Propriedade 5: o determinante de uma matriz é igual ao determinante da transposta. Dada uma matriz A, temos que

\(det\ A=det\ A^t\)

Como obter a matriz transposta?

Para obter a transposta de uma matriz A, devemos transformar as linhas de A em colunas e as colunas de A em linhas.

• Exemplo:

Determine a transposta da matriz \(A=\left[\begin{matrix}1&-6\\5&2\\4&0\\\end{matrix}\right]\).

Resolução:

Como a ordem da matriz A é 3x2, a ordem da transposta de A será 2x3. Ainda, cada linha de A será coluna de A^t e cada coluna de A será linha de A^t. Portanto,

\(A^t=\left[\begin{matrix}1&5&4\\-6&2&0\\\end{matrix}\right]\)

Perceba que cada elemento a_ij da matriz A ocupa a posição ji na matriz A^t. Por exemplo, o elemento a₁₂= -6 em A ocupa a posição na segunda linha e primeira coluna na matriz A^t.

O que é matriz simétrica?

Uma matriz quadrada D é chamada de matriz simétrica se for igual à sua transposta \((D=D^t)\). Assim, D é simétrica se \(a_{ij}=a_{ji}\) para todos os valores de i e j.

• Exemplos:

\(D\ =\ \left[\begin{matrix}2&-1\\-1&4\\\end{matrix}\right] \ e\ D^t\ =\ \left[\begin{matrix}2&-1\\-1&4\\\end{matrix}\right]\)

\(D\ =\ \left[\begin{matrix}-3&7&0\\7&4&8\\0&8&-2\\\end{matrix}\right] e\ D^t\ =\ \left[\begin{matrix}-3&7&0\\7&4&8\\0&8&-2\\\end{matrix}\right]\)

O que é matriz inversa?

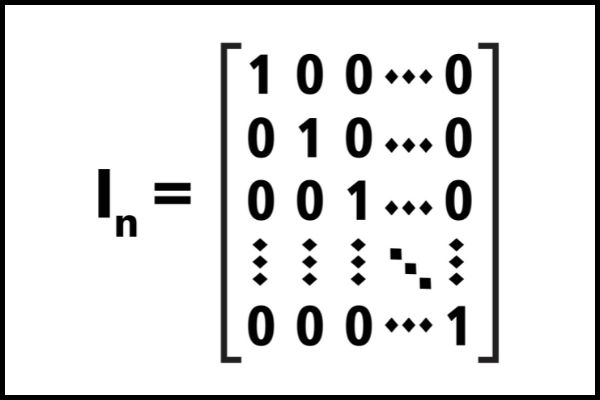
Uma matriz quadrada M^-1 é chamada de matriz inversa da matriz M se a multiplicação entre ambas resultar na matriz identidade (de mesma ordem):

\(M\cdot M^{-1}=M^{-1}\cdot M=I\)

Nesse contexto, M é uma matriz invertível, ou seja, que admite inversa.

Acesse também: Menor complementar — um número associado a cada um dos elementos da matriz

O que é matriz oposta?

Uma matriz -N é chamada de matriz oposta da matriz N se elementos na mesma posição são opostos aos de N. Lembre-se de que elementos opostos são aqueles que apresentam sinal contrário:

\( -N\ =\ \left[\begin{matrix}\ -2&\ -5\\\ -13&\ -8\\\end{matrix}\right] é\ a \ matriz \ oposta\ de\ N\ =\ \left[\begin{matrix}2&5\\13&8\\\end{matrix}\right]\)

A soma entre uma matriz e sua oposta resulta na matriz nula.

Exercícios resolvidos sobre matriz transposta

Questão 1

(UEL) Sabendo-se que a matriz

\(\left[\begin{matrix}5&x^2&2-y\\49&y&3x\\-1&-21&0\\\end{matrix}\right]\)

é igual à sua transposta, o valor de x +2y é:

A) -20

B) -1

C) 1

D) 13

E) 20

Resolução:

Alternativa B.

Note que \(a_{13}=2-y \ e\ a_{23}=3x\). Como a matriz é simétrica, temos que \(a_{13}=a_{31} \ e\ a_{23}=a_{32}\). Assim,

\(a_{13}=a_{31}\)

\(2-y=-1\)

\(y\ =\ 3\)

e

\(a_{23}=a_{32}\)

\(3x=-21\)

\(x\ =\ -7\)

Portanto,

\(x+2y=-7+2\left(3\right)=-1\)

Questão 2

(PUC) Se A, B e C são matrizes quadradas de mesma ordem e A^t, B^t e C^t são suas transpostas, a igualdade falsa entre essas matrizes é

A) \(\left(A^t\right)^t=A\)

B) \( \left(A-B\right)\cdot C=A\cdot C-B\cdot C\)

C) \( \left(A+B\right)\cdot C=A\cdot C+B\cdot C\)

D) \( \left(A+B\right)^t=A^t+B^t\)

E) \( \left(A\cdot B\right)^t=A^t\cdot B^t\)

Resolução:

Alternativa E.

De acordo com a propriedade de matriz transposta, a transposta de um produto de matrizes é igual ao produto das transpostas na ordem contrária. Ou seja,

\(\left(AB\right)^t=B^tA^t\)

Fontes

BOLDRINI, J. L. et al. Álgebra Linear. 3ª ed. São Paulo: Harper & Row do Brasil, 1980.

LIMA, Elon Lages. Álgebra Linear. Rio de Janeiro: IMPA, 2014