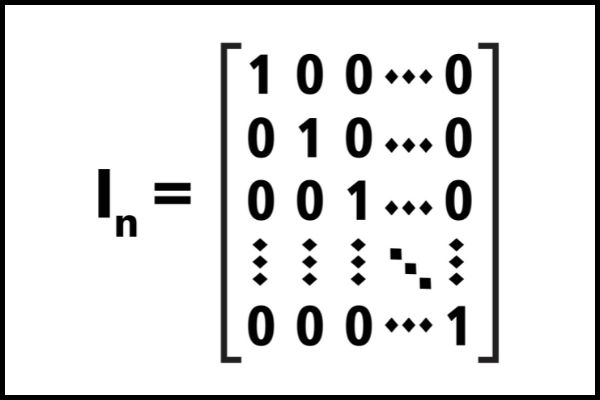
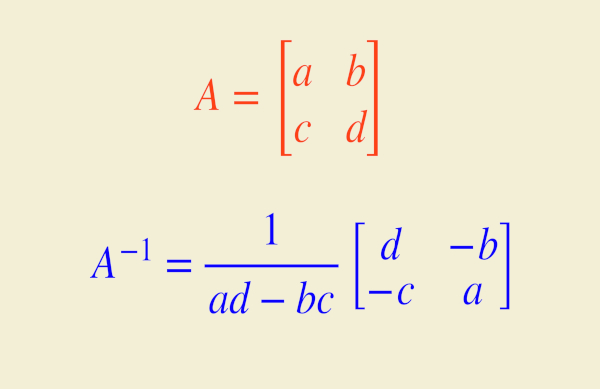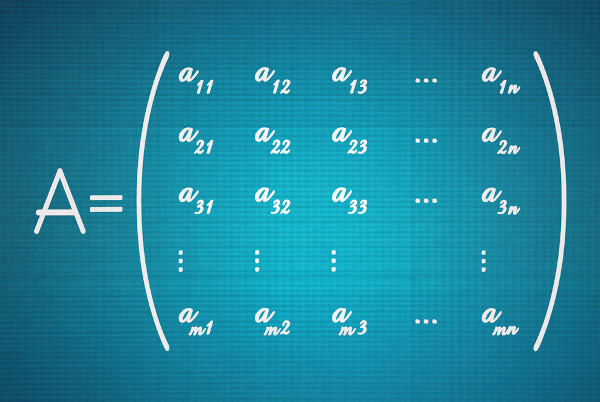A matriz identidade é a matriz quadrada que possui todos os elementos da diagonal principal iguais a 1 e todos os demais elementos iguais a 0. Representamos a matriz identidade de ordem n por In. A matriz identidade é o elemento neutro da multiplicação, ou seja, quando calculamos o produto entre a matriz A e a matriz identidade, encontramos como resposta a própria matriz A.
Tópicos deste artigo
- 1 - Resumo sobre matriz identidade
- 2 - O que é a matriz identidade?
- 3 - Quais são as propriedades da matriz identidade?
- 4 - Multiplicação da matriz identidade
Resumo sobre matriz identidade
- É a matriz quadrada que possui termos da diagonal principal iguais a 1 e os demais termos iguais a 0.
- Representamos por In a matriz identidade de ordem n.
- A matriz identidade é conhecida como elemento neutro da multiplicação, logo, A⋅In=A.
- De forma geral, a matriz identidade de ordem n é representada por:
\(I_n=\left(\begin{matrix}1&\cdots&0\\\vdots&\ddots&\vdots\\0&\cdots&1\\\end{matrix}\right)\)
O que é a matriz identidade?
A matriz identidade é um caso especial de matriz. Uma matriz é classificada como identidade quando é uma matriz quadrada que possui todos os termos da diagonal principal iguais a 1 e os demais iguais a 0.
A matriz identidade se torna um caso específico de matriz pelo fato de ser o elemento neutro da multiplicação entre matrizes, então, quando multiplicamos uma matriz A pela matriz identidade, encontramos como resposta a própria matriz A. Assim, de modo geral, temos que:
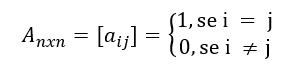
-
Exemplos de matriz identidade
Veja, a seguir, algumas matrizes identidades:
\(I_2=\left(\begin{matrix}1&0\\0&1\\\end{matrix}\right)\)
\(I_3=\left(\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right)\)
\(I_4=\left(\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\\\end{matrix}\right)\)
Quais são as propriedades da matriz identidade?
Podemos destacar duas propriedades importantes da matriz identidade, vistas a seguir.
-
A matriz identidade é o elemento neutro da multiplicação de matrizes.
Quando multiplicamos uma matriz pela matriz identidade, encontramos a própria matriz, o que significa que a operação de multiplicação entre matrizes possui um elemento neutro. Assim dada a matriz A de modo geral, temos que:
\(A\cdot I_n=A\)
-
O produto de uma matriz pela sua inversa é igual à matriz identidade.
Quando realizamos a multiplicação de uma matriz A pela matriz inversa \(A^{-1}\), encontramos o elemento neutro da multiplicação de matrizes, a matriz identidade.
\(A\cdot A^{-1}=I_n\)
Multiplicação da matriz identidade
A seguir, temos a multiplicação da matriz A pela matriz identidade. Supondo que a matriz A seja uma matriz de ordem 3:
\(A=\left[\begin{matrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{matrix}\right]\)
Queremos calcular o produto entre a matriz A e a matriz identidade I3:
\(A\cdot I_3=\left[\begin{matrix}a_{11}&a_{21}&a_{31}\\a_{21}&a_{22}&a_{32}\\a_{31}&a_{32}&a_{33}\\\end{matrix}\right]\cdot\left[\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right]\)
Supondo que M = A⋅I3, os termos de M são:
\(M_{11}=a_{11}\cdot1+a_{12}\cdot0+a_{13}\cdot0=a_{11}\)
\(M_{12}=a_{11}\cdot0+a_{12}\cdot1+a_{13}\cdot0=a_{12}\)
\(M_{13}=a_{11}\cdot0+a_{12}\cdot0+a_{13}\cdot1=a_{13}\)
\(M_{21}=a_{21}\cdot1+a_{22}\cdot0+a_{23}\cdot0=a_{21}\)
\(M_{22}=a_{21}\cdot0+a_{22}\cdot1+a_{13}\cdot0=a_{22}\)
\(M_{23}=a_{21}\cdot0+a_{22}\cdot0+a_{23}\cdot1=a_{23}\)
\(M_{31}=a_{31}\cdot1+a_{32}\cdot0+a_{33}\cdot0=a_{31}\)
\(M_{32}=a_{31}\cdot0+a_{12}\cdot1+a_{13}\cdot0=a_{32}\)
\(M_{33}=a_{31}\cdot1+a_{32}\cdot0+a_{33}\cdot1=a_{33}\)
Podemos concluir que:
\(A\cdot I_3=\left[\begin{matrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{matrix}\right]\)
Note que encontramos a mesma matriz A de modo geral, independentemente dos termos da matriz.
Veja também: Matriz triangular — a matriz em que os elementos acima ou abaixo da diagonal principal são nulos
Exercícios resolvidos sobre matriz identidade
Questão 1
Analisando as matrizes a seguir, marque a alternativa que contém a matriz identidade \(I_2\).
A) \( \left[\begin{matrix}0&1\\1&0\\\end{matrix}\right]\)
B) \( \left[\begin{matrix}1&1\\1&1\\\end{matrix}\right]\)
C) \( \left[\begin{matrix}4&1\\1&5\\\end{matrix}\right]\)
D) \( \left[\begin{matrix}1&0\\0&1\\\end{matrix}\right]\)
E) \( \left[\begin{matrix}1&2\\2&1\\\end{matrix}\right]\)
Resolução:
Alternativa D
A matriz identidade de ordem 2 possui os elementos da diagonal secundária iguais a 0 e os termos da diagonal principal iguais a 1, o que acontece na alternativa D.
Questão 2
(Udesc) Sendo a matriz \(\left[\begin{matrix}x^2-6x+9&0\\x^2-3x-4&1\\\end{matrix}\right]\) igual à matriz identidade de ordem 2, o valor de 2x é:
A) -4
B) 6
C) 4
D) 8
E) -8
Resolução:
Alternativa D
Como essa matriz é a matriz identidade, então temos que:
\(x² – 6x + 9 = 1\)
\(x² – 6x + 9 – 1= 0\)
\(x² – 6x + 8 = 0\)
Seja a = 1, b = -6 e c = 8, resolveremos a equação do 2ºgrau:
\(\Delta=b^2-4ac\)
\(\Delta=\left(-6\right)^2-4\cdot1\cdot8\)
\(\Delta=36-32\)
\(\Delta=4\)
Calculando Bhaskara:
\(x=\frac{-b\pm\sqrt\Delta}{2a}\)
\(x=\frac{6\pm\sqrt4}{2\cdot1}\)
\(x=\frac{6\pm2}{2}\)
\(x_1=\frac{6+2}{2}=\frac{8}{2}=4\)
\(x_2=\frac{6-2}{2}=\frac{4}{2}=2\)
Na outra equação, temos que:
\(x² – 3x – 4 = 0\)
\(a = 1, b = -3 e c = -4\)
Assim:
\(\Delta=\left(-3\right)^2-4\cdot1\cdot(-4)\)
\(\Delta=9+16\)
\(\Delta=25\)
Calculando Bhaskara:
\(x=\frac{-b\pm\sqrt\Delta}{2a}\)
\(x=\frac{3\pm\sqrt{25}}{2\cdot1}\)
\(x=\frac{3\pm5}{2}\)
\(x_1=\frac{3+5}{2}=\frac{8}{2}=4\)
\(x_2=\frac{3-5}{2}=\frac{-2}{2}=-1\)
Então o valor solução de ambas as equações é x = 4, logo, o valor de 2x é:
\(2\cdot4=8\)