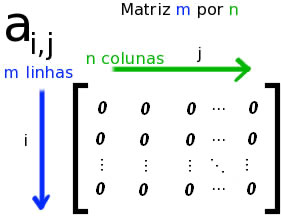
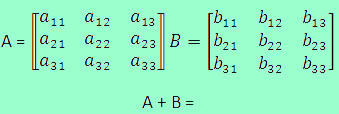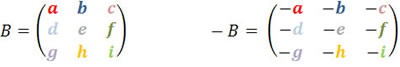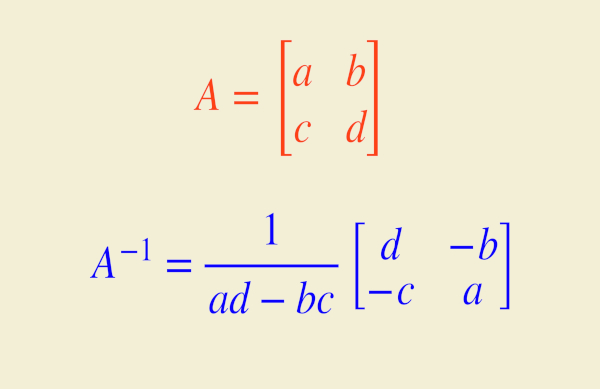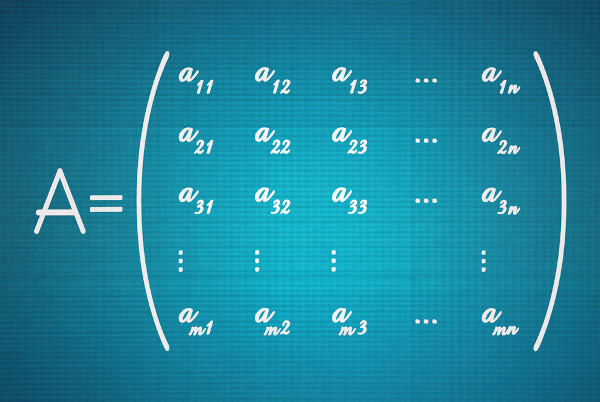A compreensão da matriz diagonal é simples e bem relacionada com as matrizes triangulares, pois os elementos que analisaremos são: diagonal principal, elementos superiores e inferiores à diagonal principal.
No estudo das matrizes triangulares, notamos que podemos ter dois tipos de matrizes: matriz triangular superior ou matriz triangular inferior, conforme podemos visualizar no exemplo abaixo:
.png)
Veja que a matriz triangular tem um condicional importante na sua definição, o condicional “ou”. Ele faz com que as duas situações não ocorram simultaneamente em uma matriz. Caso ocorram, não estarão dentro das definições de matrizes triangulares.
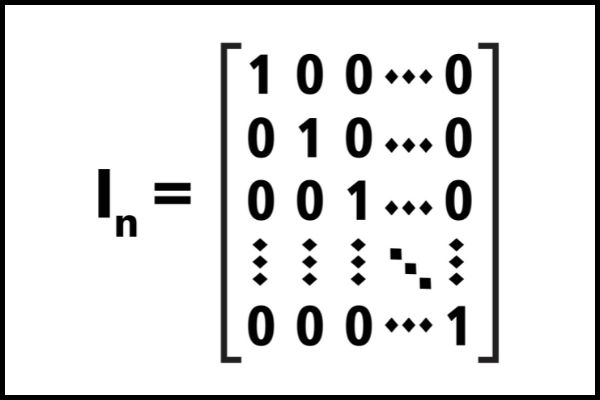
Sendo assim, como definiríamos um caso que foge à regra das matrizes triangulares? Pois bem, sabemos que podemos, sim, ter uma matriz na qual os elementos acima e abaixo da diagonal principal são nulos, um exemplo conhecido disso é a matriz identidade.
Para abarcar essas matrizes cujos únicos elementos não nulos são os elementos da diagonal principal, temos as matrizes diagonais. Para melhor compreensão, veja alguns exemplos de matrizes diagonais:
.png)
Transcrevendo essa definição matemática para uma linguagem formal e generalizada da matemática, teremos a seguinte condição:
![]()
Aproveite para conferir nossa videoaula sobre o assunto: