A matemática financeira é a área da Matemática que investiga o comportamento do dinheiro, principalmente em relação ao tempo. Movimentações comerciais (como a compra e venda de produtos e serviços) e financeiras (como empréstimos e investimentos) fazem parte do conjunto de conceitos e ferramentas que integram a matemática financeira.
Leia também: O que é o imposto de renda?
Tópicos deste artigo
- 1 - Resumo sobre matemática financeira
- 2 - O que a matemática financeira estuda?
- 3 - Fórmulas importantes da matemática financeira
- 4 - Importância da matemática financeira
- 5 - Exercícios resolvidos sobre matemática financeira
Resumo sobre matemática financeira
-
A matemática financeira é o ramo da Matemática que estuda a variação do dinheiro no tempo.
-
Alguns conceitos importantes da matemática financeira são: acréscimo, desconto, despesa, receita, lucro, juros (simples e compostos) e montante.
-
Para calcular os juros simples produzidos a partir de um capital C, aplicado a uma taxa i por um tempo t, utilizamos a fórmula
\(J = C ⋅i ⋅t\)
-
Para calcular o montante a juros compostos produzido a partir de um capital C, aplicado a uma taxa i por um tempo t, utilizamos a fórmula
\(M=C⋅(1+i)^t\)
-
A matemática financeira possui grande importância em relação à organização responsável da vida financeira.
O que a matemática financeira estuda?
A matemática financeira é a área da Matemática que estuda a dinâmica do dinheiro, principalmente em relação ao tempo. Alguns tópicos de estudo da matemática financeira são:
-
lucros;
-
receitas e despesas (fluxo de caixa);
-
juros simples e compostos;
-
taxas de juros;
-
investimentos;
-
empréstimos.
Conceitos importantes da matemática financeira
→ Acréscimo e desconto
-
Acréscimo
Acréscimo é um aumento de determinado valor calculado a partir de uma porcentagem sobre o valor.
Exemplo:
Um produto custava R$ 50 no mês de novembro. Qual o preço desse produto em dezembro, sabendo que houve um acréscimo de 20%?
Resolução:
Em dezembro, o preço do produto será a soma entre o valor original (R$ 50) e a porcentagem aplicada sobre esse valor (20% de R$ 50). Vamos representar por x o preço do produto em dezembro.
\(x=50+\frac{20}{100}⋅50\)
\(x = 50 + 10\)
\(x = 60\ reais\)
-
Desconto
Desconto é uma redução de determinado valor calculada a partir de uma porcentagem sobre o valor.
Exemplo:
Antes de uma campanha promocional, um produto custava R$ 60. Se a promoção oferece 10% de desconto em qualquer item, qual o valor desse produto durante a campanha?
Resolução:
Durante a campanha promocional, o valor do produto é a diferença entre o preço original (R$ 60) e a porcentagem aplicada sobre esse valor (10% de R$ 60). Vamos representar com y o preço do produto durante a campanha.
\(y=60-\frac{10}{100}⋅60\)
\(y = 60 - 6\)
\(y = 54\ reais\)
→ Despesa, receita e lucro
-
Despesa
A despesa é o recurso financeiro gasto. Em uma empresa, salários de funcionários, impostos e custos de produção são exemplos de despesas.
-
Receita
A receita é o recurso financeiro arrecadado. Em uma empresa, as vendas de produtos ou serviços são exemplos de receitas.
-
Lucro
O lucro é a diferença entre as receitas e as despesas.
→ Juros (simples e compostos) e montante
Juro é um valor agregado a uma quantia de dinheiro após um período de tempo. Em compras a prazo, por exemplo, é comum que sejam aplicados juros às parcelas, principalmente se estiverem em grande quantidade (ou seja, se o tempo para quitar a dívida for muito longo).
-
Juros simples
Caso os juros sejam calculados sobre o valor inicial da operação financeira, chamamos de juros simples. Assim, os juros simples constituem um valor fixo.
-
Juros compostos
Caso os juros sejam calculados sobre o valor acumulado do período anterior (ou seja, juros sobre juros), chamamos de juros compostos.
-
Montante
Montante é a soma entre o valor inicial (também conhecido como capital inicial) e os juros de uma operação financeira.
Importante: Além desses conceitos, a matemática financeira também abrange o estudo da razão, proporção, regra de três, porcentagem e interpretação de tabelas e gráficos.
Fórmulas importantes da matemática financeira
→ Fórmula dos juros simples
Os juros simples (símbolo J) de uma operação financeira são calculados pela seguinte fórmula:
\(J = C ⋅i ⋅t\)
-
C → capital (valor) inicial.
-
i → taxa de juros.
-
t → tempo (período).
O montante de uma operação no regime de juros simples é
\(M = C + J\)
\(M = C + C ⋅i ⋅t\)
\(M=C⋅1+i⋅t\)
→ Fórmula dos juros compostos
O montante de uma operação no regime de juros compostos é calculado pela seguinte fórmula:
\(M=C⋅(1+i)^t\)
-
C → capital (valor) inicial.
-
i → taxa de juros.
-
t → tempo (período).
No contexto de juros compostos, o capital inicial também é conhecido como valor presente (VP em português ou PV, present value, em inglês) e o montante, como valor futuro (VF em português ou FV, future value, em inglês).
Importante: As unidades da taxa de juros e do tempo devem ser compatíveis. Se o tempo estiver expresso em meses, a taxa deve ser ao mês (a.m.); se o tempo estiver expresso em anos, a taxa deve ser ao ano (a.a.) e assim por diante. Isso vale tanto para a fórmula dos juros simples quanto para a fórmula dos juros compostos.
Veja também: Como funcionam os juros de cheque especial e de cartão de crédito?
Importância da matemática financeira
As trocas comerciais, a utilização de serviços e os financiamentos são alguns exemplos de movimentações financeiras. Nessas situações, conhecer os fundamentos da matemática financeira permite a tomada de decisões financeiras de forma consciente e responsável, seja pela elaboração de um planejamento ou pelo reconhecimento de possíveis tentativas de golpes e fraudes.
Exercícios resolvidos sobre matemática financeira
Questão 1
(Enem) Um administrador resolve estudar o lucro de sua empresa e, para isso, traça o gráfico da receita e do custo de produção de seus itens, em real, em função da quantidade de itens produzidos.
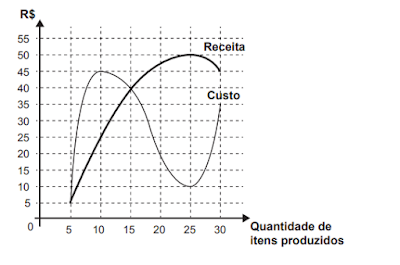
O lucro é determinado pela diferença: receita - custo.
O gráfico que representa o lucro dessa empresa, em função da quantidade de itens produzidos, é
A)
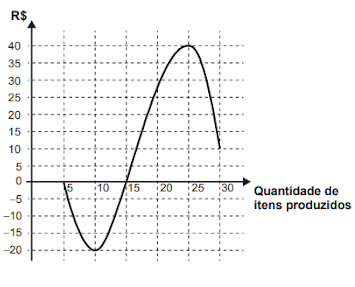
B)
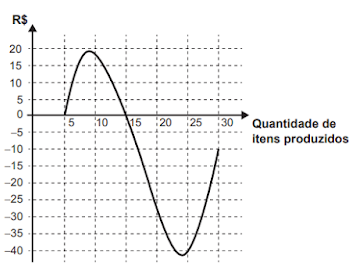
C)
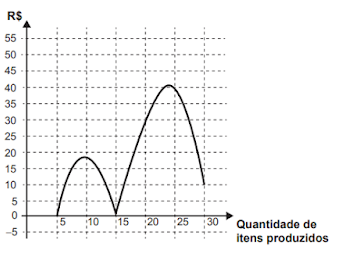
D)
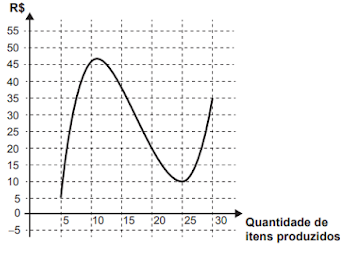
E)
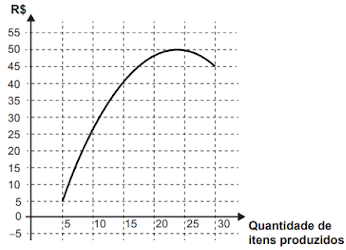
Resolução:
Alternativa A.
Quando a quantidade de itens produzidos varia de 5 até 15, o custo é superior à receita. Assim, o lucro é negativo nesse intervalo. Note que quando a quantidade é igual a 10, o custo começar a diminuir, enquanto a receita continua aumentando. Portanto, o lucro deve aumentar a partir desse ponto.
Quando a quantidade de itens produzidos é exatamente 15, o custo é igual à receita. Assim, o lucro é igual a zero nesse ponto.
Quando a quantidade de itens produzidos varia de 15 a 30, a receita é superior ao custo. Assim, o lucro é positivo nesse intervalo. Note que quando a quantidade é igual a 25, o custo começar a aumentar, enquanto a receita começa a diminuir. Portanto, o lucro deve diminuir a partir desse ponto. O gráfico que apresenta esse comportamento corresponde à alternativa A.
Questão 2
(Encceja) Uma pessoa necessita de um empréstimo de R$ 10 000,00. Uma instituição financeira oferece empréstimos a uma taxa de juros simples de 2% ao mês, sendo que a dívida gerada pelo empréstimo deve ser liquidada em uma única parcela, paga ao final do último mês do contrato.
Essa pessoa pretende pagar, no máximo, R$ 11 000,00 na liquidação dessa dívida.
O prazo máximo, em quantidade de meses, que deverá durar esse contrato é
A) 5.
B) 50.
C) 500.
D) 550.
Resolução:
Alternativa A.
O montante do empréstimo deve ser no máximo R$ 11 000,00. Assim, como se trata de juros simples, com C = 10000 e i = 2% = 0,02, temos que
\(M=C⋅1+i⋅t\)
\(11000=10000⋅1+0,02⋅t\)
\(11000=10000 + 200t\)
\(1000 = 200t\)
\(t = 5\ meses\)













