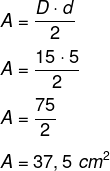O losango é uma figura plana que possui quatro lados, todos congruentes. Na geometria plana, ele é considerado um caso particular de quadrilátero, possuindo propriedades importantes.
Por ser um quadrilátero, o losango possui duas diagonais: a diagonal menor e a diagonal maior. Elas se cruzam de forma perpendicular, o que torna possível a aplicação do teorema de Pitágoras, relacionando o comprimento do lado e a metade do comprimento de cada uma das diagonais do losango.
Essa forma geométrica possui fórmulas específicas para o cálculo de área e de perímetro. Para calcular a área do losango, calculamos a metade do produto entre a diagonal maior e a diagonal menor. Já o perímetro pode ser calculado pela multiplicação da medida do lado por quatro.
Leia também: Quais são as principais diferenças entre figuras planas e espaciais?
Tópicos deste artigo
- 1 - Elementos do losango
- 2 - Propriedades do losango
- 3 - Perímetro do losango
- 4 - Área do losango
- 5 - Exercícios resolvidos
Elementos do losango

Conhecemos como losango todo quadrilátero que possui os quatro lados congruentes. Os principais elementos do losango são:
-
os lados;
-
os vértices;
-
os ângulos internos;
-
a diagonal maior; e
-
a diagonal menor.
As diagonais são os segmentos que ligam dois vértices não consecutivos. Há duas diagonais no losango. Chamamos de D o comprimento da diagonal maior e de d o comprimento da diagonal menor.
Como o losango é um quadrilátero, ele possui:
-
4 lados;
-
4 ângulos internos;
-
4 vértices.
Veja a imagem a seguir com os principais elementos do losango:
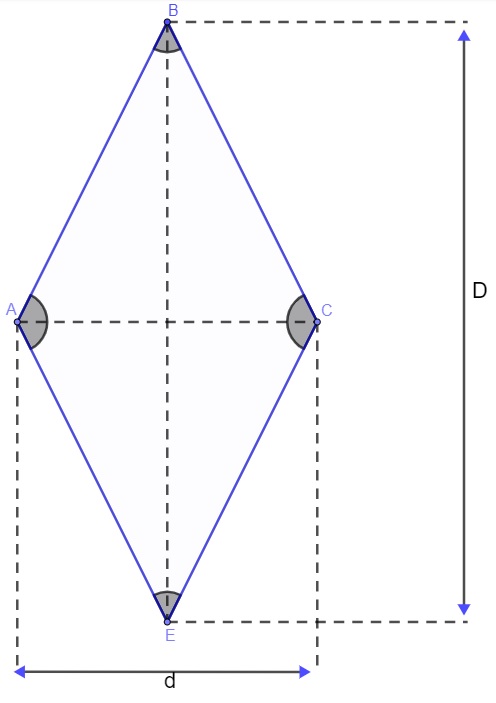
d → comprimento da diagonal menor
D → comprimento da diagonal maior
A,B,C e E → vértices
AB, AE, CE e BC → lados do losango
Propriedades do losango
O losango é um quadrilátero e também um paralelogramo. Assim, ele possui propriedades herdadas dessas classificações, além de propriedades específicas.
Como ele é um paralelogramo, o losango possui:
-
ângulos e lados opostos congruentes;
-
soma dos ângulos internos igual a 360º;
-
lados opostos paralelos e congruentes;
-
diagonais que se cruzam no ponto médio;
-
ângulos consecutivos suplementares, ou seja, com soma igual a 180º.
Além dessas propriedades já existentes para todo paralelogramo, há uma propriedade que é exclusiva do losango: as diagonais são perpendiculares entre si. Ao traçar a diagonal maior e a diagonal menor, elas se cruzam de forma perpendicular.
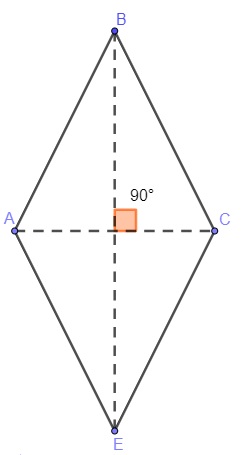
Há uma consequência importante dessa propriedade, que é a relação pitagórica entre a medida dos lados e a metade das medidas da diagonal.
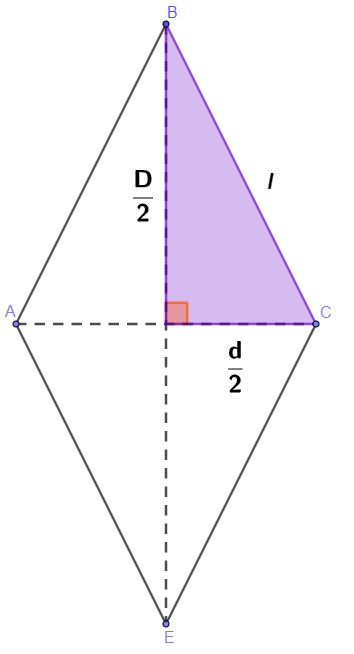
Pelo triângulo retângulo, aplicando o teorema de Pitágoras, temos que:
![]()
Veja também: Qual é a condição de existência de um triângulo?
Perímetro do losango
O perímetro de um polígono é o comprimento do seu contorno. No losango, nós sabemos que os quatro lados são congruentes. Assim, para calcular o perímetro dessa figura plana, basta multiplicar a medida do lado por quatro.
P = 4l
Exemplo:
Encontre o perímetro do losango sabendo que um dos lados mede 7,5 centímetros.
Para calcular o perímetro, basta multiplicar o comprimento do lado por 4.
P = 4 · 7,5
P = 30 centímetros.
Área do losango
Na maioria dos polígonos, o cálculo da área está relacionado com o comprimento da base e da altura, mas, no losango em particular, como ele não possui base, calculamos a sua área utilizando os comprimentos das diagonais. Assim, a área do losango é calculada pelo produto entre as diagonais dividido por dois.
![]()
D → diagonal maior
d → comprimento da diagonal menor
Exemplo: Qual é a área do losango que possui diagonal maior igual a 4 centímetros e diagonal menor igual 3 centímetros?
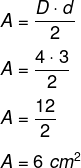
Exercícios resolvidos
Questão 1 - Um terreno possui o formato de um losango, conforme a imagem a seguir, com as medidas dadas em metros.
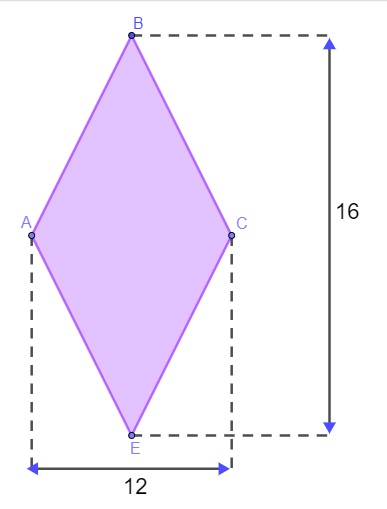
Para cercar o terreno, Matheus precisa saber qual é o perímetro desse losango. Para que ele não precise ir até o terreno realizar a medida dos lados, ele utilizou a propriedade do losango para encontrar o seu perímetro. Supondo que ele tenha acertado, o valor encontrado para o perímetro desse terreno é:
A) 100 metros.
B) 10 metros.
C) 12 metros.
D) 120 metros.
E) 150 metros.
Resolução
Alternativa D.
Note que o comprimento do lado não é conhecido, então utilizaremos a relação pitagórica para encontrar o lado desse losango.
Calculando a metade do comprimento de cada uma das diagonais:
D = 16 → D/ 2 = 8
d = 12 → d/2 = 6
Então, sabemos que:
l² = 8² + 6²
l² = 64 + 36
l² = 100
l = √100
l = 10 metros
Agora é possível calcular o perímetro:
P = 4l
P = 4 · 30
P = 120 metros
Questão 2 - Qual é a área de um losango que possui diagonal maior de 15 centímetros e diagonal menor no valor de um terço da diagonal maior?
A) 37,5 cm²
B) 35 cm²
C) 75 cm²
D) 70 cm²
E) 45 cm²
Resolução
Alternativa A.
Considere:
d → comprimento da diagonal menor;
D → comprimento da diagonal maior.
Sabendo que a diagonal menor mede 1/3 da diagonal maior, então, para encontrar o comprimento d, basta dividir D por três:
D = 15 d = 15/ 3 = 5
Agora calculando a área, temos que: