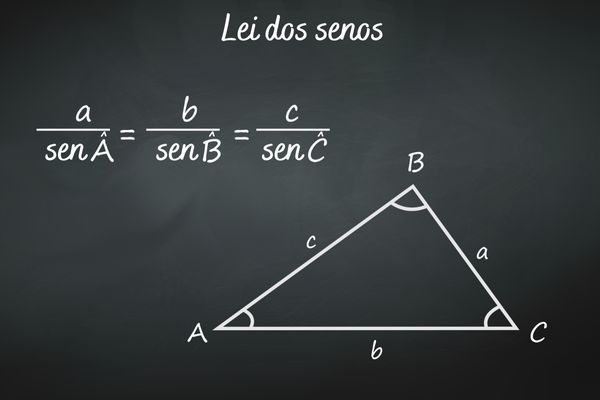
A lei dos senos é uma relação métrica entre as medidas dos lados e dos ângulos do triângulo. Ela serve para encontrarmos tanto um ângulo quanto um lado desconhecido do triângulo, sendo utilizada principalmente para o cálculo do lado.
Essa lei demonstra que há uma proporcionalidade entre a medida do lado do triângulo e o seno do ângulo interno desse triângulo, pois a medida do lado de um triângulo dividida pelo seno do ângulo que está oposto a esse lado é igual à medida de um outro lado divido pelo respectivo seno do ângulo oposto, o que nos permite descobrir valores desconhecidos tanto de ângulo quanto de lado no triângulo.
Saiba mais: O que são equações trigonométricas?
Tópicos deste artigo
- 1 - Resumo sobre lei dos senos
- 2 - Videoaula sobre lei dos senos
- 3 - O que é seno?
- 4 - O que diz a lei dos senos?
- 5 - Fórmula da lei dos senos
- 6 - Aplicação da lei dos senos
- 7 - Lei dos senos no triângulo retângulo
- 8 - Quando a lei dos senos é aplicada?
- 9 - Exercícios resolvidos sobre lei dos senos
Resumo sobre lei dos senos
-
A lei dos senos pode ser conhecida também como teorema dos senos.
-
Utilizamos a lei dos senos para encontrar a medida de um lado e de um ângulo desconhecido no triângulo.
-
Para aplicar a lei dos senos, é necessário conhecer a medida de dois ângulos internos e de um lado do triângulo.
-
A fórmula da lei dos senos de um triângulo ABC é:
\(\frac{a}{senÂ}=\frac{b}{sen\hat{B}}=\frac{c}{sen\hat{C}}\)
Videoaula sobre lei dos senos
O que é seno?
O seno é a razão entre o cateto oposto e a hipotenusa do triângulo retângulo e está entre as principais razões trigonométricas em um triângulo retângulo. Quando consideramos o triângulo retângulo de raio 1, podemos determinar o valor do seno para todos os ângulos no estudo da Trigonometria no círculo trigonométrico. O seno é utilizado para encontrar valores desconhecidos em um triângulo devido à sua proporcionalidade.
De modo geral, o seno de um ângulo do triângulo retângulo é calculado por:
\(sen\ α=\frac{cateto\ oposto\ de\ α}{hipotenusa\ de\ α}\)
O que diz a lei dos senos?
A lei dos senos é conhecida também como teorema dos senos e demonstra que existe proporcionalidade entre a medida do lado de um triângulo qualquer e o ângulo oposto a esse lado. Na lei dos senos, é demonstrado que a razão entre a medida do lado e o seno do seu ângulo oposto é sempre constante para o triângulo.
Fórmula da lei dos senos
Considere um triângulo ABC:
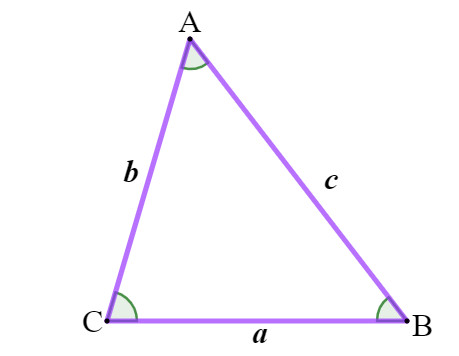
Considerando esse triângulo, a fórmula da lei dos senos é a seguinte:
\(\frac{a}{senÂ}=\frac{b}{sen\hat{B}}=\frac{c}{sen\hat{C}}\)
Aplicação da lei dos senos
Veja a seguir um exemplo da aplicação da lei dos senos.
-
Exemplo:
Dado o triângulo a seguir, encontre a medida x:
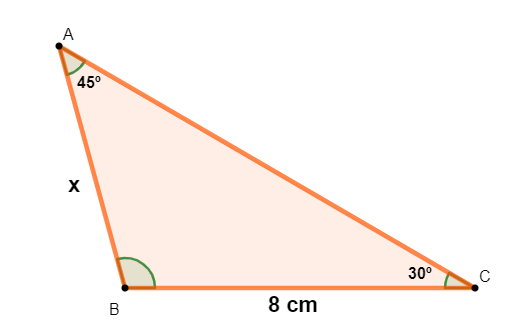
Resolução:
Aplicando a lei dos senos:
\(\frac{8}{sen45°}=\frac{x}{sen30°}\)
\(8\cdot sen\ 30° = x\cdot sen\ 45°\)
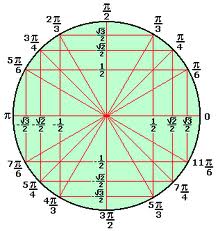
Consultando a tabela dos ângulos notáveis, sabemos que:
\(sen30°=\frac{1}2\)
\(sen45°=\frac{\sqrt2}2\)
Então, temos que:
\(8⋅\frac{1}2=x⋅\frac{\sqrt2}2\)
\(\frac{8}2=\frac{x\sqrt2}2\)
\(4⋅2=x\sqrt2\)
\(8=x\sqrt2\)
\(x=\frac{8}{\sqrt2}\)
Racionalizando a fração:
\(x =\frac{8}{\sqrt2}⋅\frac{\sqrt2}{\sqrt2}\)
\(x=\frac{8\sqrt2}2\)
\(x=4\sqrt2\)
Assim, sabemos que o lado x mede \(4\sqrt2\) cm.
Lei dos senos no triângulo retângulo
Podemos aplicar lei dos senos em um triângulo retângulo:
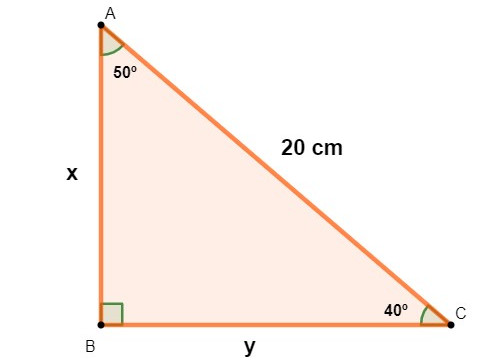
Analisando o triângulo, temos que:
\(\frac{x}{sen40°}=\frac{y}{sen50°}=\frac{20}{sen90°}\)
Sabemos que o seno de 90° é 1, logo:
\(\frac{y}{sen50°}=20\)
Consultando a tabela trigonométrica:
\(sen50° = 0,77\)
Portanto:
\(y=20 ⋅0,77\)
\(y=15,4\)
Agora, calculando o valor de x:
\(\frac{x}{sen40°}=20\)
\(x=20 ⋅0,64\)
\(x=12,8\)
Quando a lei dos senos é aplicada?
A lei dos senos normalmente é aplicada em triângulos não retângulos quando conhecemos dois ângulos e a medida de um dos lados do triângulo. Apesar disso, não significa que a lei dos senos não possa ser utilizada para triângulos que são retângulos. Quando o triângulo é retângulo, existem métodos mais simples que nos permitem encontrar o valor de lados desconhecidos, como a aplicação das razões trigonométricas, por exemplo.
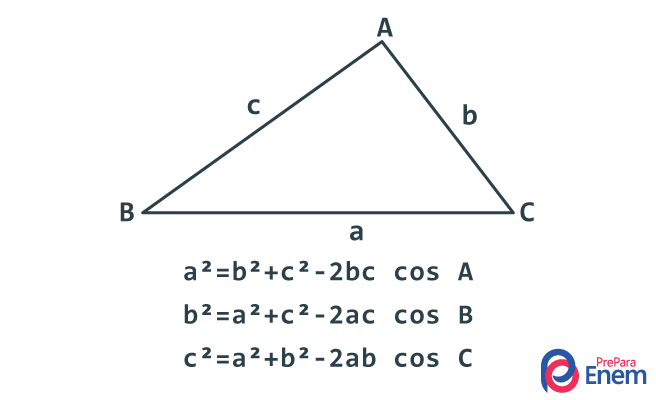
Interessante: Além da lei dos senos, existe a lei dos cossenos, que é aplicada em triângulos não retângulos cuja medida de dois lados e de um ângulo é conhecida, e a intenção é encontrar a medida do outro lado.
Saiba também: O que são transformações trigonométricas?
Exercícios resolvidos sobre lei dos senos
Questão 1
Paulo comprou um terreno no formato de um triângulo, como o da imagem a seguir:
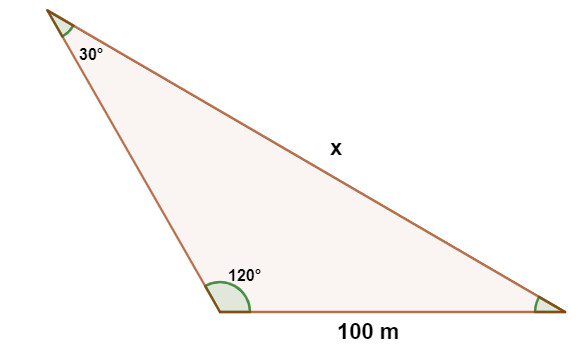
Utilizando 1,7 como aproximação para \(\sqrt3\), o valor de x é aproximadamente:
A) 120 m
B) 160 m
C) 170 m
D) 240 m
E) 340 m
Resolução:
Alternativa C
Aplicando a lei dos senos:
\(\frac{100}{sen30°}=\frac{x}{sen120°}\)
\(x ⋅sen\ 30° = 100 ⋅sen\ 120°\)
\(x⋅\frac{1}2=100⋅\frac{\sqrt3}2\)
\(\frac{x}2=\frac{100⋅1,7}2\)
\(x=170\)
Questão 2
(Enem) Para calcular a distância entre duas árvores, representadas pelos pontos A e B, situadas em margens opostas de um rio, foi escolhido um ponto C arbitrário, na margem onde se localiza a árvore A. As medidas necessárias foram tomadas, e os resultados obtidos foram os seguintes: AC = 70 m, BAC = 62° e ACB = 74°. Sendo cos 28° = 0,88, sen 74° = 0,96 e sen 44° = 0,70, podemos afirmar que a distância entre as árvores é:
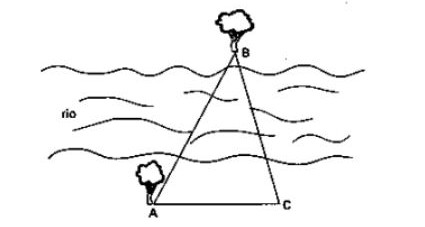
A) 48 metros
B) 78 metros
C) 85 metros
D) 96 metros
E) 102 metros
Resolução:
Alternativa D
Sabemos que a soma dos ângulos internos de um triângulo é de 180°. Se um ângulo mede 74° e o outro 62°, então o outro ângulo mede:
180 – 74 – 62 = 44°
Aplicando a lei dos senos:
\(\frac{70}{sen44°}=\frac{x}{sen74°}\)
\(x⋅sen44° = 70 ⋅sen74°\)
\(x⋅0,7 = 70 ⋅0,96\)
\(0,7x=67,2\)
\(x=\frac{67,2}{0,7}\)
\(x=96\ metros\)