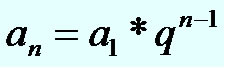As progressões geométricas são sequências numéricas que apresentam uma característica em comum: cada elemento, a partir do segundo, é obtido realizando o produto entre o termo anterior e uma constante q, denominada de razão da PG. Podemos notar a utilização das progressões em diversas áreas do conhecimento. Os pitagóricos já haviam descoberto, por exemplo, que na escala musical, os valores das frequências das sequências de notas de uma oitava, formam uma progressão geométrica.
Dentre os tópicos abordados no estudo da PG, temos a interpolação de meios geométricos. Interpolar meios geométricos entre dois números dados, a1 e an, é acrescentar números entre os dois que já foram dados para que a sequência numérica formada seja uma PG. Para realizar a interpolação de meios geométricos basta conhecer o valor da razão da progressão geométrica e utilizar a fórmula do termo geral:
an = a1?q(n-1)
Onde,
a1 → é o primeiro termo da PG.
an → é o último termo da PG.
n → é o número dos termos da PG.
Vejamos alguns exemplos para melhor compreensão:
Exemplo 1. Interpole cinco meios geométricos entre 7 e 5103.
Solução: Interpolar cinco meios geométricos entre 7 e 5103 equivale a dizer que devemos acrescentar cinco números entre 7 e 5103 para que a sequência formada seja uma PG.
(7, _, _, _, _, _, 5103)
Para isso, devemos encontrar o valor da razão dessa PG. Pela análise do exercício, temos que:
a1 = 7 e a7 = 5103 e n = 7 (pois a sequência apresenta 7 termos).
Utilizando a fórmula do termo geral, obtemos:

Conhecendo o valor da razão da PG podemos determinar os cinco termos que devem ficar compreendidos entre 7 e 5103.
a2 = a1*q = 7*3 = 21
a3 = a2*q = 21*3 = 63
a4 = a3*q = 63*3 = 189
a5 = a4*q = 189*3 = 567
a6 = a5*q = 567*3 = 1701
Portanto, interpolando cinco meios geométricos entre 7 e 5103, obtemos a PG:
(7, 21, 63, 189, 567, 1701, 5103)
Exemplo 2. Distribua 4 números entre 800 e 25 para que a sequência numérica formada seja uma progressão geométrica.
Solução: Queremos interpolar 4 meios geométricos entre 800 e 25.
(800, _, _, _, _, 25)
Precisamos conhecer o valor da razão dessa PG. Para isso, utilizaremos a fórmula do termo geral.
Sabemos que: n = 6, a1 = 800 e a6 = 25. Segue que:

Conhecido o valor da razão, podemos determinar os termos que devem ficar compreendidos entre 800 e 25.
a2 = a1*q = 800*0,5 = 400
a3 = a2*q = 400*0,5 = 200
a4 = a3*q = 200*0,5 = 100
a5 = a4*q = 100*0,5 = 50
Portanto, interpolando 4 meios geométricos entre 800 e 25, obtemos a seguinte PG:
(800, 400, 200, 100, 50, 25)