Hipérbole

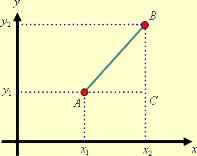
O estudo da hipérbole foi iniciado pelo matemático Apolônio, que desenvolveu um trabalho muito respeitado sobre as seções cônicas. Ele analisou, além da hipérbole, a parábola e a elipse, que podem ser obtidas a partir de cortes efetuados em um cone. Na figura a seguir temos a representação analítica da hipérbole:

Confira a representação analítica da hipérbole

Na figura anterior, a hipérbole está representada pelo conjunto de pontos presentes nas curvas em vermelho. Os pontos que compõem a hipérbole apresentam uma característica em comum. Dados quaisquer dois pontos, o módulo da diferença das distâncias entre eles e os pontos F₁ e F₂ é sempre igual à distância de 2a entre A₁ e A₂. Considere P e Q como pontos pertencentes à hipérbole. De forma simplificada, temos:

Vejamos agora os elementos principais da hipérbole:

• Centro: O;

• Focos: F₁ e F_2;

• Distância focal: segmento entre F₁ e F₂. A distância focal vale 2c;

• Vértices da hipérbole: A₁ e A_2;

• Eixo real ou transverso: segmento entre A₁ e A₂. O eixo real mede 2a;

• Eixo Imaginário: segmento entre B₁ e B_2. Sua medida é de 2b;

• Excentricidade da hipérbole: quociente entre c e a (^c/_a).

Na imagem estão destacados todos os principais pontos da hipérbole

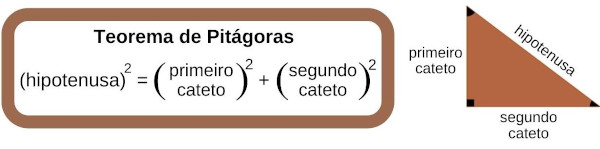
Observe na figura acima que se formou um triângulo retângulo com lados a, b e c. Aplicando o Teorema de Pitágoras, podemos estabelecer uma relação notável, válida para qualquer hipérbole:

c² = a² + b²

Há situações em que teremos a = b na hipérbole. Nesse caso, ela será classificada como equilátera.

1ª Equação reduzida da hipérbole:

Há situações em que o eixo real e os focos da hipérbole estarão sobre o eixo x, em um sistema cartesiano ortogonal, como podemos ver na figura a seguir:

Para hipérboles semelhantes a essa, utilizamos a 1ª equação reduzida

Nesse caso, teremos uma equação reduzida da hipérbole. Considere P (x, y) como um ponto qualquer contido na hipérbole, logo:

x² – y² = 1
a²    b²      

2ª Equação Reduzida da Hipérbole:

Há situações em que lidamos com uma hipérbole que possui o eixo real e os focos sobre o eixo y. Veja a figura a seguir:

Para hipérboles semelhantes a essa, utilizamos a 2ª equação reduzida

Nesse caso, utilizamos outra equação reduzida da hipérbole. Novamente considere P(x, y) como um ponto qualquer contido na hipérbole, logo:

y² – x² = 1
a²    b²