O hexágono é um polígono que possui 6 lados. Ele pode ser regular, ou seja, possuir todos os lados congruentes, ou irregular, isto é, possuir pelo menos um lado com medida diferente.
Quando o hexágono é regular, cada um dos seus ângulos internos mede 120°, e independentemente de ser regular ou irregular, a soma dos seus ângulos internos é de 720°. Além disso, quando o hexágono é regular, ele possui fórmula específica para o cálculo da sua área, do seu apótema e do seu perímetro. Já quando o hexágono não é regular, não existe uma fórmula específica.
Leia também: Paralelogramo — figura que possui os lados opostos paralelos entre si
Tópicos deste artigo
- 1 - Resumo sobre hexágono
- 2 - O que é hexágono?
- 3 - Elementos do hexágono
- 4 - Quais são os tipos de hexágono?
- 5 - Quais as propriedades do hexágono?
- 6 - Fórmulas do hexágono regular
- 7 - Prisma de base hexagonal
- 8 - Pirâmide de base hexagonal
- 9 - Hexágono inscrito em uma circunferência
- 10 - Hexágono circunscrito a uma circunferência
- 11 - Exercícios resolvidos sobre hexágono
Resumo sobre hexágono
-
O hexágono é um polígono que possui 6 lados.
-
A soma dos ângulos internos de um hexágono é de 720°.
-
O hexágono é regular se possuir todos os ângulos internos congruentes e todos os lados congruentes.
-
Em um hexágono regular, cada ângulo interno mede 120°.
-
Há fórmulas específicas para calcular a área, o perímetro e o apótema do hexágono regular.
-
A fórmula para calcular a área de um hexágono regular de lado l é:
\(A=3\cdot\frac{l^2\sqrt3}{2}\)
-
O perímetro de um hexágono regular de lado l é calculado por:
\(P=6l\)
-
Para calcular o apótema do hexágono regular de lado l, utilizamos a fórmula:
\(a=\frac{\sqrt3}{2}\cdot l\)
O que é hexágono?
O hexágono é um tipo de polígono, ou seja, uma figura plana fechada por poligonais. Um polígono é classificado como hexágono quando ele possui 6 lados. Sabemos que a figura plana que possui 6 lados possui também 6 ângulos internos.
Elementos do hexágono
Os principais elementos de um polígono são os seus lados, ângulos internos e vértices. Todo hexágono possui 6 lados, 6 ângulos e 6 vértices.
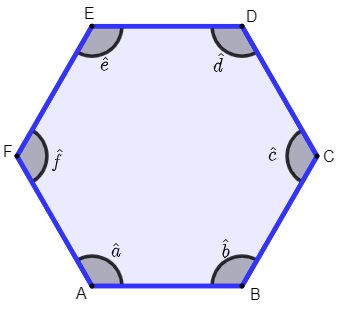
-
Os vértices do hexágono são os pontos A, B, C, D, E, F.
-
Os lados são os segmentos \(\overline{AB},\overline{BC},\overline{CD},\overline{DE},\overline{EF},\overline{AF}\).
-
Os ângulos são \(â, \hat{b},\hat{c},\hat{d},ê,\hat{f}\).
Quais são os tipos de hexágono?
Os hexágonos podem ser separados em dois grupos: os que são classificados como irregulares e os que são classificados como regulares.
-
Hexágono regular: um hexágono é considerado regular quando as medidas dos seus lados são todas congruentes, ou seja, todos os lados possuem a mesma medida.
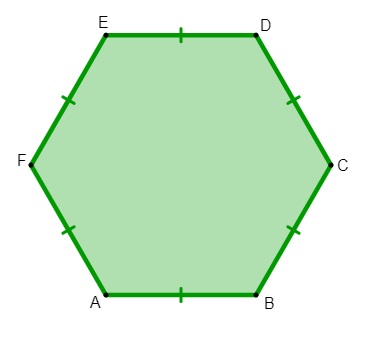
-
Hexágono irregular: um hexágono é considerado irregular quando ele não possui todos os lados com a mesma medida.
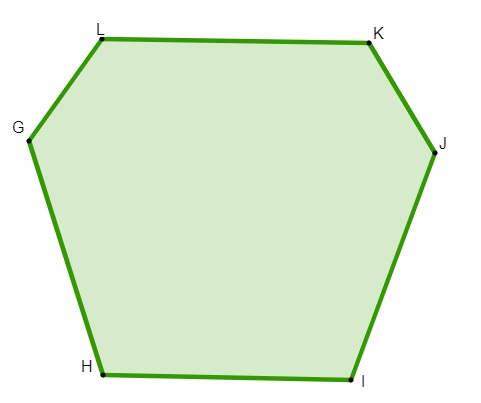
Quais as propriedades do hexágono?
As principais propriedades do hexágono são:
-
A soma dos ângulos internos de um hexágono é de 720°.
Para calcular a soma dos ângulos internos de um polígono, utilizamos a fórmula:
\(\textbf{S}_\textbf{i}=\left(\textbf{n}-\mathbf{2}\right)\cdot\textbf{180°}\)
Como n é o número de lados do polígono, substituindo n = 6, temos que:
\(S_i=\left(6-2\right)\cdot180°\)
\(S_i=4\cdot180°\)
\(S_i=720°\)
-
Os ângulos internos de um hexágono regular medem 120° cada.
Como o hexágono regular possui ângulos congruentes, dividindo 720 por 6, temos que 720° : 6 = 120°, ou seja, cada ângulo interno de um hexágono regular mede 120°.
-
Um hexágono possui um total de 9 diagonais.
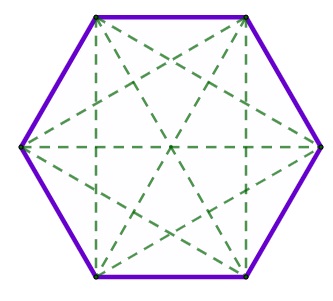
O número de diagonais de um polígono pode ser calculado pela fórmula:
\(d=\frac{(n-3)·n}2\)
Como há 6 lados, temos que:
\(d=\frac{(6-3)·6}2\)
\(d=\frac{3\cdot6}{2}\)
\(d=\frac{18}{2}\)
\(d=9\)
Leia também: Polígonos regulares — grupo que possui lados com medidas iguais e ângulos congruentes
Fórmulas do hexágono regular
A seguir, veremos fórmulas que são exclusivas para os cálculos da área, perímetro e apótema do hexágono regular. O hexágono irregular não possui fórmulas específicas, pois isso depende diretamente da forma que o hexágono assume. Portanto, o hexágono regular é o mais comum e mais importante para a Matemática, já que possui fórmulas específicas.
-
Perímetro do hexágono
O perímetro de um hexágono é igual à soma de todos os seus lados. Quando o hexágono é irregular, somamos as medidas de cada um dos seus lados para encontrar o perímetro. Porém, quando o hexágono é regular com lado medindo l, para calcular seu perímetro basta utilizar a fórmula:
\(P=6l\)
Exemplo:
Calcule o perímetro de um hexágono regular que possui um dos lados medindo 7 cm.
Resolução:
P = 6l
P = 6 ⋅ 7
P = 42 cm
-
Apótema do hexágono
O apótema de um polígono regular é o segmento de reta que vai do centro do polígono até o ponto médio de um dos lados desse polígono.
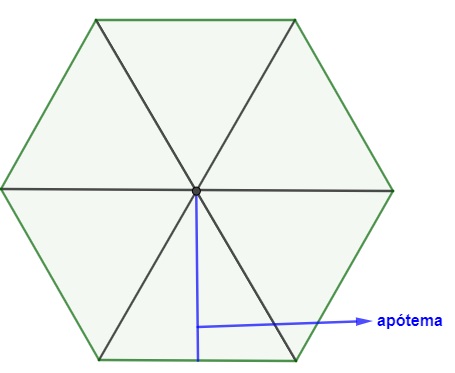
Quando traçamos os segmentos dos vértices até o centro do hexágono, ele é dividido em 6 triângulos equiláteros. Então para calcular o apótema, utilizamos a mesma fórmula utilizada para calcular a altura do triângulo equilátero:
\(a=\frac{l\sqrt3}{2}\)
Exemplo:
Um hexágono possui lado medindo 8 cm. Assim, o comprimento do seu apótema é de:
Resolução:
Dado l = 8, temos que:
\(a=\frac{8\sqrt3}{2}\)
\(a=4\sqrt3\)
-
Área do hexágono
Existe uma fórmula para calcular a área de um hexágono regular. Como vimos anteriormente, é possível dividir o hexágono regular em 6 triângulos equiláteros. Dessa forma, multiplicamos a área do triângulo equilátero por 6 para encontrar a área do hexágono. A fórmula da área do hexágono é:
\(A=6\cdot\frac{l^2\sqrt3}{4}\)
Simplificando por 2, temos que:
\(A=3\cdot\frac{l^2\sqrt3}{2}\)
Exemplo:
Qual é a área do hexágono que possui lado medindo 6 cm?
Resolução:
Substituindo l por 6, temos que:
\(A=3\cdot\frac{6^2\sqrt3}{2}\)
\(A=3\cdot\frac{36\sqrt3}{2}\)
\(A=3\cdot18\sqrt3\)
\(A=54\sqrt3cm^2\)
Prisma de base hexagonal
O hexágono está presente também em figuras espaciais, logo é essencial conhecer as fórmulas do hexágono regular para o estudo dos sólidos geométricos. Veja a seguir o prisma de base hexagonal.
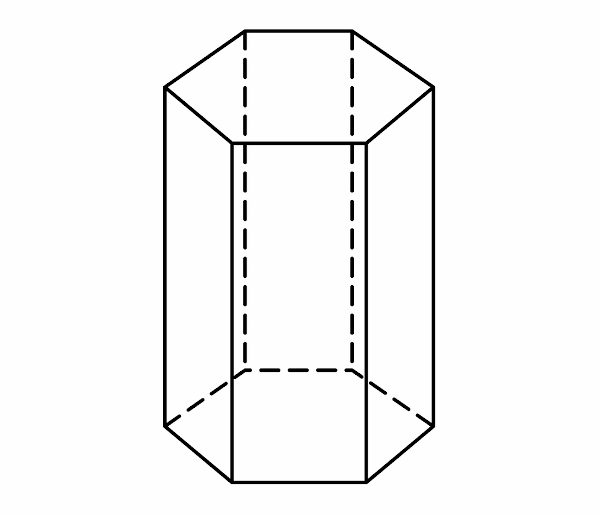
O valor do volume do prisma é obtido pela multiplicação entre a área da base e a altura. Como a base é um hexágono regular, o volume de um prisma de base hexagonal pode ser calculado pela fórmula:
\(V=3\cdot\frac{L^2\sqrt3}{2}\cdot h\)
Pirâmide de base hexagonal
O hexágono pode estar também na base de pirâmides, as pirâmides de base hexagonal.
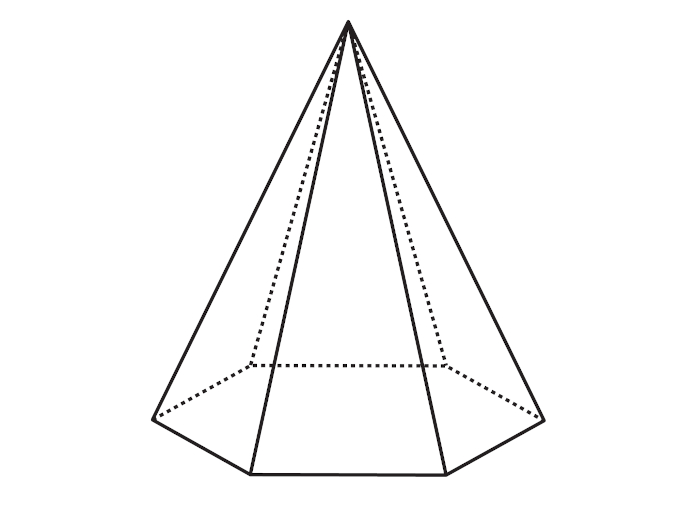
Para calcular o volume de uma pirâmide que tem como base um hexágono regular, é essencial saber como calcular a área da base do hexágono. O volume da pirâmide, de modo geral, é igual ao produto entre a área da base e a altura dividido por 3. Como a área da base é igual à área do hexágono, temos que:
\(V=3\cdot\frac{l^2\sqrt3}{2}\cdot\frac{h}{3}\)
Simplificando a fórmula, o volume de uma pirâmide de base hexagonal pode ser calculado por:
\(V=\frac{l^2\sqrt3h}{2}\)
Leia também: Principais diferenças entre figuras planas e espaciais
Hexágono inscrito em uma circunferência
O hexágono regular pode ser representado dentro da circunferência, ou seja, inscrito em uma circunferência. Quando representamos o hexágono regular dentro da circunferência, o raio dela é igual ao comprimento do lado.
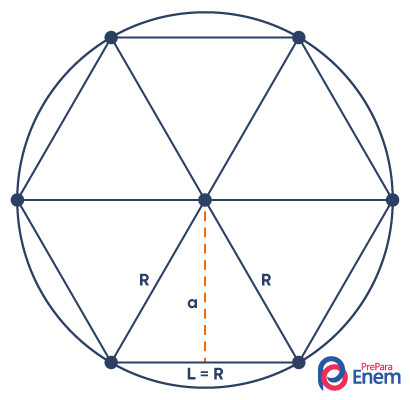
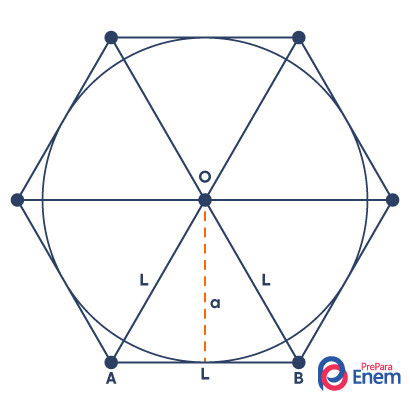
Hexágono circunscrito a uma circunferência
O polígono fica circunscrito quanto representamos uma circunferência contida dentro desse polígono. No hexágono regular, é possível representar essa circunferência de modo que o seu raio seja igual ao apótema do hexágono:
Exercícios resolvidos sobre hexágono
Questão 1
Uma região possui formato de um hexágono regular. Sabendo que o lado desse hexágono mede 3 metros e utilizando \(\sqrt3\) = 1,7, podemos afirmar que a área dessa região é de:
A) \(18\ m^2\)
B) \(20,5{\ m}^2\)
C) \(22,95\ m^2\)
D) \(25{\ m}^2\)
E) \(27,22\ m^2\)
Resolução:
Alternativa C
Calculando a área, temos que:
\(A=3\cdot\frac{l^2\sqrt3}{2}\)
\(A=3\cdot\frac{3^2\cdot1,7}{2}\)
\(A=3\cdot\frac{9\cdot1,7}{2}\)
\(A=3\cdot\frac{15,3}{2}\)
\(A=\frac{45,9}{2}\)
\(A=22,95\ m^2\)
Questão 2
(Aeronáutica) Dado um hexágono regular de 6 cm de lado, considere o seu apótema medindo a cm e o raio da circunferência a ele circunscrita medindo R cm. O valor de (R + \(a\sqrt3\)) é:
A) 12
B) 15
C) 18
D) 25
Resolução:
Alternativa B
O raio da circunferência circunscrita é igual à medida do lado, ou seja, R = 6. Já o apótema é calculado por:
\(a=\frac{l\sqrt3}{2}=\frac{6\sqrt3}{2}=3\sqrt3\)
Então, temos que:
\(\left(6+3\sqrt3\cdot\sqrt3\right)\)
\(\ 6+3\cdot3\)
\(6+9\ \)
\(15\)








