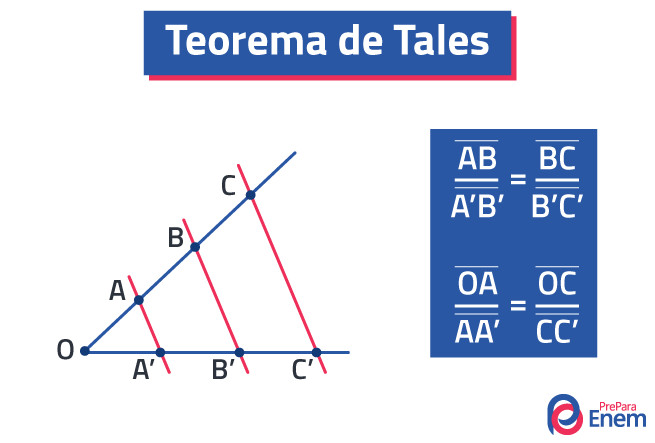
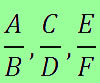Grandezas diretamente proporcionais são aquelas que apresentam uma relação de proporção de forma direta, isto é, à medida que o valor de uma grandeza aumenta, o valor da outra grandeza também aumenta na mesma proporção. O mesmo acontece quando o valor de uma das grandezas diminuir: a outra também vai diminuir na mesma proporção. Aumentar ou diminuir na mesma proporção quer dizer que se uma grandeza aumenta k vezes, a outra também aumentará k vezes.
Podemos perceber a presença de grandezas diretamente proporcionais frequentemente no nosso cotidiano. Por exemplo, se uma quilometragem rodada aumentar, o consumo de combustível também aumentará na mesma proporção, e caso a quilometragem rodada passe a ser o dobro em comparação à quilometragem anterior, o consumo de combustível também será o dobro.
Leia também: Razão entre grandezas diferentes
Tópicos deste artigo
- 1 - O que são grandezas diretamente proporcionais?
- 2 - Exemplos de grandezas diretamente proporcionais
- 3 - Como se calculam as grandezas diretamente proporcionais?
- 4 - Diferença entre grandezas diretamente e inversamente proporcionais
- 5 - Exercícios resolvidos sobre grandezas diretamente proporcionais
O que são grandezas diretamente proporcionais?
Primeiramente, vamos compreender o que é grandeza. Grandeza é tudo aquilo que pode ser medido, como a massa, comprimento, velocidade, valor monetário, volume, área.
Há situações em que é possível relacionar mais de uma grandeza, por exemplo, o consumo de combustível de um veículo e a quilometragem que ele percorre, o peso da verdura e o valor a ser pago por ela, o número de pedidos de um produto e o tempo gasto para atender a esses pedidos, o número de motoristas que dirigem alcoolizados e o número de acidentes, a velocidade e o tempo gasto para percorrer determinada distância. Enfim, estamos cercados de grandezas que se relacionam, e essa relação pode ser diretamente proporcional, inversamente proporcional ou pode até mesmo ter relação, mas não ter proporção.
Dizemos que duas grandezas são diretamente proporcionais quando ao comparar situações diferentes envolvendo-as, o valor delas aumenta ou diminui na mesma proporção.
Exemplos de grandezas diretamente proporcionais
-
O peso da verdura e o valor pago: Sabemos que existe um valor pago pelo quilo. Se o cliente pegar mais que 1 kg, o valor pago aumentará também, de forma proporcional. Por exemplo, se o cliente levar 1,5 kg, ele pagará o valor referente a 1 kg mais metade desse valor. O mesmo acontece se o cliente levar a metade de 1 kg: o valor pago também será a metade. Note aí que as grandezas peso e preço aumentam ou diminuem na mesma proporção.
-
Quantidade de produtos e o lucro: Se uma empresa vende certo produto e em determinado período ela vende mais desse produto, o lucro que ela vai receber também aumentará na mesma proporção. Ou seja, se ela vender o dobro da quantidade do produto, por exemplo, o lucro também será o dobro, pois este está diretamente ligado à quantidade de produto vendido e de forma proporcional.
-
Quilometragem percorrida e consumo de combustível: O consumo de combustível é diretamente proporcional à quilometragem percorrida, pois se triplicarmos a quilometragem, por exemplo, triplicaremos o consumo de combustível.
-
Gravidade e peso: A força peso é a massa vezes a força da gravidade. Sendo assim, quanto maior a gravidade, maior será o peso. Logo, essas grandezas são diretamente proporcionais.
Como se calculam as grandezas diretamente proporcionais?
Quando há grandezas que são diretamente proporcionais, podemos encontrar valores desconhecidos para determinadas situações. Por exemplo, se sabemos quantos quilômetros um carro faz com um litro, podemos calcular quantos litros serão necessários para fazer uma viagem maior, utilizando a propriedade fundamental da proporção.
A propriedade fundamental da proporção mostra que se a, b, c, e d são proporcionais, temos que:
\(\frac{a}{b}=\frac{c}{d}\)
Exemplo:
Matias percebeu que durante a semana ele percorre 96 quilômetros e gasta um total de 8 litros de combustível. Para fazer uma viagem da sua cidade até o sítio dos seus avós e depois do sítio dos seus avós até a sua casa novamente, ele percorrerá o total de 336 quilômetros. Nessas condições, qual será a quantidade necessária de combustível?
Resolução:
Montaremos uma igualdade entre duas razões. Na primeira, colocaremos a razão entre a grandeza quilômetros e na segunda, a razão entre a grandeza volume, já que essas grandezas são proporcionais. Sabemos que 96 divido por 336 é igual a 8 divido por x, sendo x a quantidade de combustível necessária para a viagem:
\(\frac{96}{336}=\frac{8}{x}\)
Multiplicando cruzado:
\(96x=8⋅336\)
\(96x=2688\)
\(x=\frac{2688}{96}\)
\(x=28\)
Serão necessários 28 litros para percorrer 336 quilômetros.
Saiba mais: Regra de três simples com grandezas diretamente proporcionais
Diferença entre grandezas diretamente e inversamente proporcionais
Quando analisamos a relação entre duas grandezas, outro caso bastante recorrente é o de grandezas que são inversamente proporcionais. A diferença entre grandezas diretamente proporcionais e grandezas inversamente proporcionais é que no segundo caso, à medida que o valor de uma grandeza aumenta, o valor da outra diminui na mesma proporção, ou seja, se comporta de forma inversa. Velocidade e tempo, por exemplo, são grandezas que se comportam de forma inversamente proporcionais, pois, supondo que em uma distância fixa a velocidade para fazer um percurso aumentar, o tempo gasto será menor e se dará na mesma proporção, pois se a velocidade for o dobro, o tempo cairá pela metade.
Exercícios resolvidos sobre grandezas diretamente proporcionais
Questão 1
(Enem 2012) Uma mãe recorreu à bula para verificar a dosagem de um remédio que precisava dar a seu filho. Na bula, recomendava-se a seguinte dosagem: 5 gotas para cada 2 kg de massa corporal a cada 8 horas. Se a mãe ministrou corretamente 30 gotas do remédio a seu filho a cada 8 horas, então a massa corporal dele é de
A) 12 kg.
B) 16 kg.
C) 24 kg.
D) 36 kg.
E) 75 kg.
Resolução:
Alternativa A
Sabemos que a quantidade de gotas é proporcional ao peso. Sendo x a massa corporal dele, temos que:
\(\frac{2}{x}=\frac{5}{30}\)
Multiplicando cruzado:
\(5x=2⋅30\)
\(5x=60\)
\(x=\frac{60}{5}\)
\(x=12\)
A massa corporal é de 12 kg.
Questão 2
(Enem 2015) Um pesquisador, ao explorar uma floresta, fotografou uma caneta de 16,8 cm de comprimento ao lado de uma pegada. O comprimento da caneta (c), a largura (L) e o comprimento (C) da pegada, na fotografia, estão indicados no esquema.
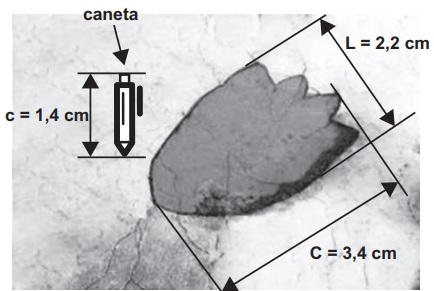
A largura e o comprimento reais da pegada, em centímetros, são, respectivamente, iguais a
A) 4,9 e 7,6.
B) 8,6 e 9,8.
C) 14,2 e 15,4.
D) 26,4 e 40,8.
E) 27,5 e 42,5.
Resolução:
Alternativa D
Sabemos que o tamanho real é diretamente proporcional ao tamanho da imagem na fotografia, pois quanto maior o tamanho real, maior será o tamanho na fotografia. Então, sendo x o tamanho real da largura e y o tamanho real do comprimento, calculando a largura, temos que:
\(\frac{16,8}{1,4}=\frac{x}{2,2}\)
\(1,4x=2,2⋅16,8\)
\(1,4x=36,96\)
\(x=\frac{36,96}{1,4}\)
\(x=26,4\)
Calculando o comprimento:
\(\frac{16,8}{1,4}=\frac{y}{3,4}\)
\(1,4y=3,4⋅16,8\)
\(1,4y=57,12\)
\(y=\frac{57,12}{1,4}\)
\(y=40,8\)
O comprimento e largura em centímetros são, respectivamente, 26,4 e 40,8.