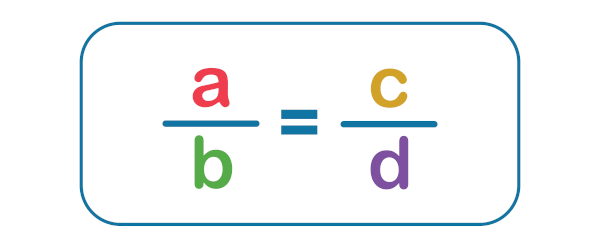Uma grandeza é um ente que está relacionado às medidas dos objetos. Não aos objetos em si, mas aos tipos de medidas que podem ser observadas neles. Em uma barra de metal, por exemplo, é possível perceber diversas grandezas: comprimento, massa (peso), volume etc. Assim, as grandezas não são as medidas, os objetos que podem ser medidos ou os objetos usados para medir, mas aquilo que dá nome à medida que está sendo observada.
Duas grandezas proporcionais podem apresentar essa proporcionalidade de forma direta ou inversa. Antes de discutir esse tema, é importante lembrar o que são proporções.
Tópicos deste artigo
Grandezas diretamente proporcionais
É pelo fato de duas grandezas serem proporcionais que, quando há variação dos valores de uma delas, os valores da outra também variam na mesma proporção.
Então, dadas as grandezas A e B, dizemos que elas são diretamente proporcionais quando o aumento na medida da grandeza A implica em um aumento na medida da grandeza B, na mesma proporção. Também existe a possibilidade em que, considerando as grandezas A e B diretamente proporcionais, diminuir a medida da grandeza A implica em diminuir a medida da grandeza B, na mesma proporção.
Exemplo: uma empresa produz 500 peças por dia com seus 14 funcionários. Se aumentarmos o número de funcionários, o número de peças produzidas por dia deverá aumentar também, por consequência e na mesma proporção. Suponha que a empresa contrate outras 14 pessoas, dobrando, assim, o número de funcionários. O número de peças produzidas também dobrará e passará a ser 1000 por dia.
Grandezas inversamente proporcionais
Dadas as grandezas A e B, dizemos que elas são inversamente proporcionais quando um aumento na medida da grandeza A faz com que a medida da grandeza B diminua na mesma proporção, ou vice-versa.
Exemplo: suponha que uma fábrica de sapatos produza uma determinada quantidade de pares, a cada 12 horas, com 24 funcionários. Se aumentarmos o número de funcionários, o número de horas gastas para produzir essa mesma quantidade de pares diminuirá. Agora, considere que a fábrica tenha contratado outros 24 funcionários. Como o número de funcionários dobrou, o tempo para a produção da mesma quantidade de sapatos cairá pela metade, passando a ser igual a 6 horas.
Regra de três
A regra de três é o método usado para descobrir uma das quatro medidas de uma proporção (entre grandezas ou não) quando as outras três são conhecidas.
Digamos que uma empresa possua 14 funcionários e produza 500 peças de um produto em determinado período de tempo. Se a diretoria dessa empresa contratar mais sete funcionários, quantas peças passam a ser produzidas no mesmo período de tempo?
Observe que o número de funcionários e o número de peças produzidas são grandezas diretamente proporcionais. Para resolver esse tipo de problema, basta montar a proporção entre as medidas apresentadas, representando aquela que queremos descobrir com alguma letra, e aplicar a propriedade fundamental das proporções.
Para que nada dê errado, prefira colocar informações relativas a uma grandeza em uma única fração e cuide para que a ordem das medidas não fique errada na proporção. Nesse exemplo, note que no segundo momento a empresa terá 14 + 7 = 21 funcionários.
14 = 500
21 x
14x = 21·500
14x = 10500
x = 10500
14
x = 750 peças.
Se as grandezas forem inversamente proporcionais, deveremos inverter uma das frações da proporção antes de aplicar a propriedade fundamental das proporções.