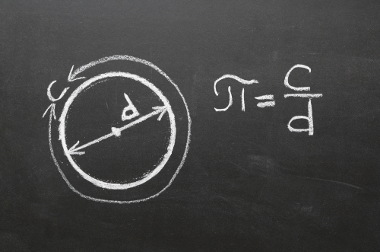Geometria plana

O estudo da geometria plana começa a partir de elementos primitivos, que são:

• o ponto;

• a reta;

• o plano.

A partir desses objetos, surgem conceitos como os de:

• ângulo;

• segmento de reta;

• semirreta;

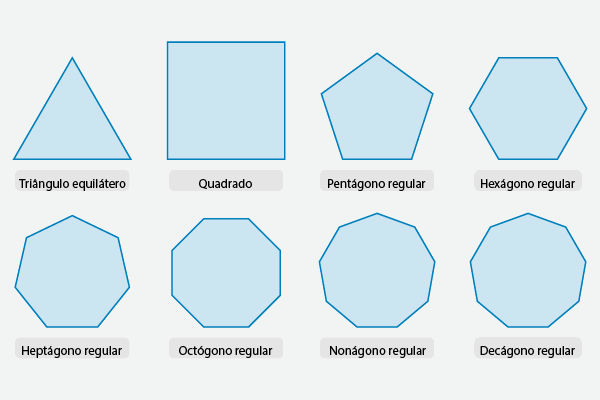
• polígonos;

• área, entre outros.

Um dos conteúdos mais recorrentes do Enem, a geometria plana aparece bastante na prova de Matemática por meio de questões que cobram desde os conteúdos básicos até os conteúdos mais avançados, como área de polígonos e o estudo de círculo e circunferência. Para se dar bem, é importante conhecer as fórmulas de área dos principais polígonos e reconhecer essas figuras.

Leia também: Posições relativas entre duas retas: paralelas, concorrentes ou coincidentes

Tópicos deste artigo

• 1 - Conceitos básicos da geometria plana
• 2 - Figuras geométricas
• 3 - Fórmulas da geometria plana
  • Triângulos
  • Quadriláteros
  • Paralelogramo
  • Retângulo
  • Losango
  • Quadrado
  • Trapézio
  • Círculo e circunferência
• 4 - Diferença entre geometria plana e geometria espacial
• 5 - Geometria plana no Enem
• 6 - Exercícios resolvidos

Conceitos básicos da geometria plana

A geometria plana é conhecida também como geometria plana euclidiana, já que foi o matemático Euclides que realizou grandes contribuições para a fundamentação dessa área de estudos. Tudo começou com três elementos primitivos: o ponto, a reta e o plano, que são assim chamados porque são elementos construídos na mente do homem de forma intuitiva e não podem ser definidos.

• Um ponto sempre é representado por meio de letras maiúsculas do nosso alfabeto.

• Uma reta é representada por letra minúscula.

• Um plano é representado por uma letra do alfabeto grego.

A partir da reta, surgem outros conceitos importantes, que são o de semirreta e o de segmento de reta.

• Semirreta: parte de uma reta que possui começo em um ponto determinado, mas não possui fim.

• Segmento de reta: parte de uma reta que possui começo e fim determinados, ou seja, é o segmento que está entre dois pontos.

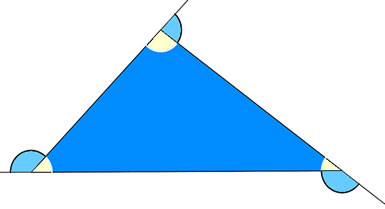
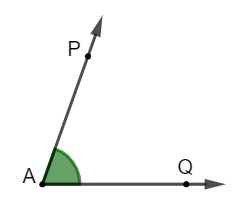
Entendendo a geometria como uma construção, é possível definir o que são ângulos agora que sabemos o que é uma semirreta. Sempre que há o encontro de duas semirretas em um ponto conhecido como vértice, a região que se encontra entre as semirretas é conhecida como ângulo.

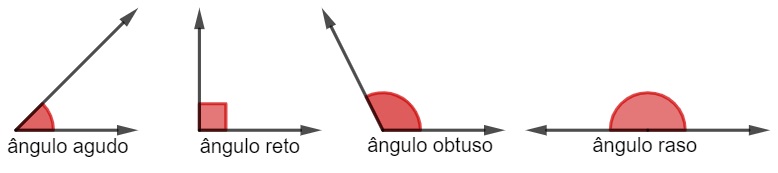
Um ângulo pode ser classificado como:

• agudo: se sua medida for menor que 90º;

• reto: se sua medida for igual a 90º;

• obtuso: se sua medida for maior que 90º e menor que 180º;

• raso: se sua medida for igual a 180º.

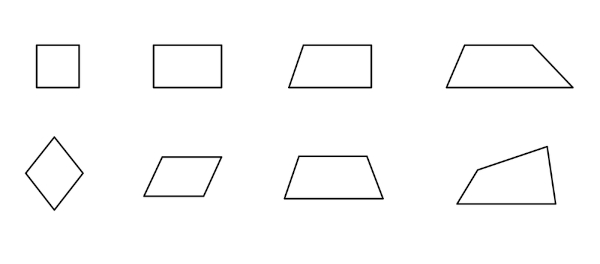
Figuras geométricas

Representações no plano de imagens são conhecidas como figuras geométricas. Existem alguns casos particulares — os polígonos — com propriedades importantes. Além dos polígonos, outra figura importante é a circunferência, que também deve ser estudada a fundo.

Veja também: Congruência de figuras geométricas – casos de figuras distintas com medidas iguais

Fórmulas da geometria plana

No caso dos polígonos, é essencial reconhecer cada um deles, suas propriedades e a sua fórmula de área e de perímetro. É importante entender que a área é o cálculo da superfície que essa figura plana possui, e o perímetro é o comprimento do seu contorno, calculado pela soma de todos os lados. Os principais polígonos são os triângulos e os quadriláteros — destes, destacam-se o quadrado, o retângulo, o losango e o trapézio.

• Triângulos

O triângulo é um polígono que possui três lados.

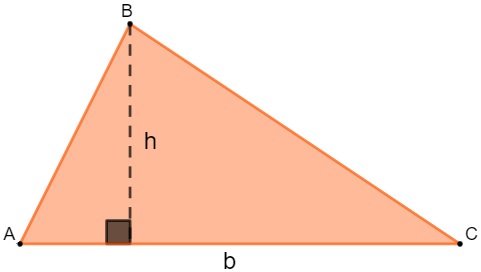
b → base
h → altura

Já o perímetro do triângulo não possui fórmula específica. Basta lembrar que ele é calculado pela adição do comprimento de todos os lados.

• Quadriláteros

Existem alguns casos específicos de quadriláteros, e cada um deles possui fórmulas específicas para calcular a área da superfície. Assim, é fundamental reconhecer cada um deles e saber aplicar a fórmula para o cálculo da área.

• Paralelogramo

Os paralelogramos são quadriláteros que possuem os lados opostos paralelos.

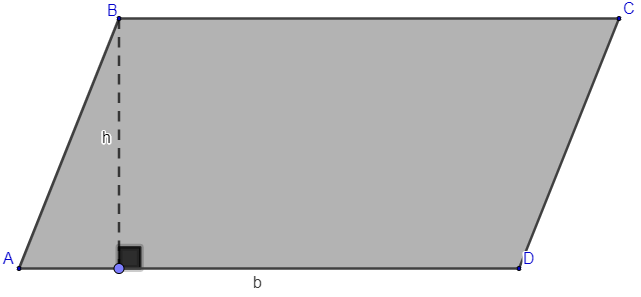
A = b · h

b → base

h → altura

No paralelogramo é importante perceber que os lados opostos são congruentes, logo o perímetro dele pode ser calculado por:

• Retângulo

O retângulo é um paralelogramo que possui todos os ângulos retos.

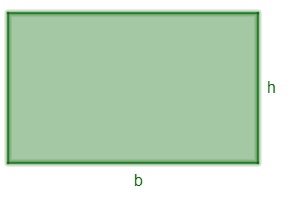
A = b · h

b → base

h → altura

Como os lados coincidem com a altura e a base, o perímetro pode ser calculado por:

P = 2 ( b + h)

• Losango

O losango é um paralelogramo que possui todos os lados congruentes.

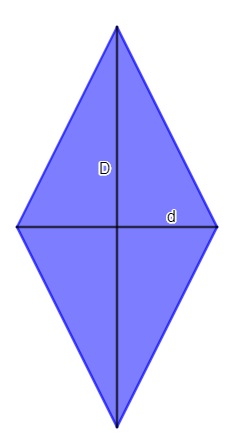
D→ diagonal maior

d → diagonal menor

Como todos os lados são congruentes, o perímetro do losango pode ser calculado por:

P = 4l

l → lado

• Quadrado

Paralelogramo que possui todos os ângulos retos e todos os lados congruentes.

A = l²

l → lado

Assim como o losango, o quadrado possui todos os lados congruentes, logo o seu perímetro é calculado por:

P = 4l

l → lado

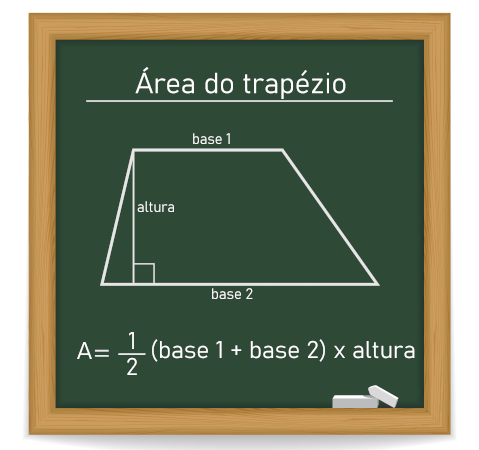
• Trapézio

Quadrilátero que possui dois lados paralelos e dois lados não paralelos.

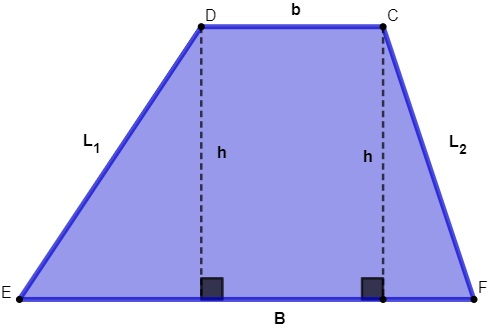
B → base maior

b → base menor

L₁ e L₂ → lados

Sobre o perímetro de um trapézio, não existe uma fórmula específica para isso. Basta lembrar que perímetro é a soma de todos os lados:

P = B + b + L₁ + L₂

• Círculo e circunferência

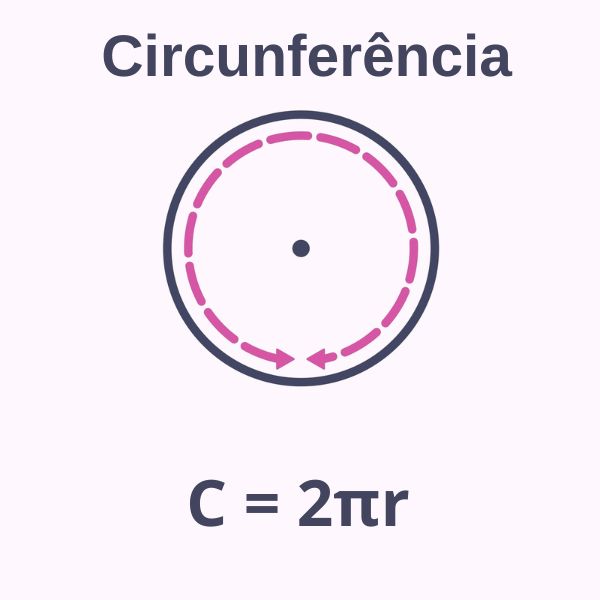
Além dos polígonos, outras figuras planas importantes são o círculo e a circunferência. Definimos como circunferência a figura formada por todos os pontos que estão a uma mesma distância (r) do centro. Essa distância é chamada de raio. Para ficar claro o que é a circunferência e o que é o círculo, basta entendermos que circunferência é o contorno que delimita o círculo, logo o círculo é a região que fica limitada pela circunferência.

Essa definição gera duas fórmulas importantes, a de área do círculo (A) e a de comprimento de circunferência (C). Conhecemos como comprimento da circunferência o que seria análogo ao perímetro de um polígono, ou seja, é o comprimento do contorno da região.

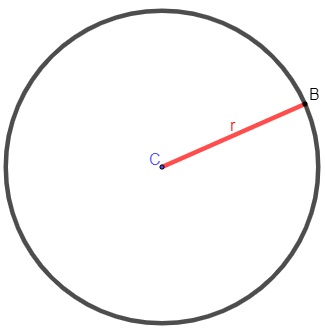
A = πr²
C = 2πr
r → raio

Leia mais: Circunferência e círculo: definições e diferenças básicas

Diferença entre geometria plana e geometria espacial

Ao comparar a geometria plana com a geometria espacial, é importante perceber que a geometria plana é bidimensional e que a geometria espacial é tridimensional. Vivemos em um mundo tridimensional, logo a geometria espacial está constantemente presente por ser uma geometria no espaço. A geometria plana, como o nome sugere, é estudada no plano, logo ela possui duas dimensões. É a partir da geometria plana que nós temos base para realizar estudos específicos da geometria espacial.

Para conseguir diferenciar bem as duas, basta realizar a comparação entre um quadrado e um cubo. O cubo possui largura, comprimento e altura, ou seja, três dimensões. Já um quadrado possui apenas comprimento e largura.

Geometria plana no Enem

A prova de matemática do Enem leva em consideração seis competências, com o objetivo de avaliar se o candidato possui habilidades específicas. A geometria plana está ligada à competência 2.

→ Competência de área 2: utilizar o conhecimento geométrico para realizar a leitura e a representação da realidade e agir sobre ela.

Nessa competência, há quatro habilidades que o Enem espera que o candidato tenha, que são:

• H6 – Interpretar a localização e a movimentação de pessoas/objetos no espaço tridimensional e sua representação no espaço bidimensional.

Essa habilidade busca avaliar se o candidato consegue fazer relação do mundo tridimensional com o mundo bidimensional, ou seja, a geometria plana.

• H7 – Identificar características de figuras planas ou espaciais.

A habilidade mais cobrada na geometria plana envolve desde características básicas, como reconhecimento de ângulos e da figura plana, até características que exigem um estudo mais aprofundado dessas figuras.

• H8 – Resolver situação-problema que envolva conhecimentos geométricos de espaço e forma.

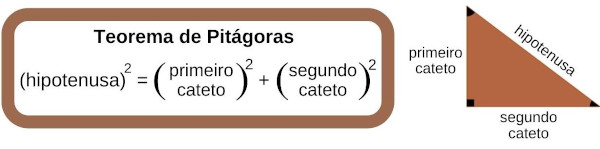
Essa habilidade envolve perímetro, área, trigonometria, entre outros assuntos mais específicos que são utilizados para resolver situações-problema contextualizadas.

• H9 – Utilizar conhecimentos geométricos de espaço e forma na seleção de argumentos propostos como solução de problemas do cotidiano.

Assim como a habilidade 8, os conteúdos podem ser os mesmos, mas, nesse caso, além da realização dos cálculos, espera-se que o candidato consiga comparar e analisar as situações para selecionar argumentos que forneçam respostas a problemas do nosso dia a dia.

Com base nessas competências, podemos afirmar tranquilamente que a geometria plana é um conteúdo que se fará presente em todas as edições da prova e, analisando os anos anteriores, sempre houve mais de uma questão sobre o assunto. Além disso, a geometria plana se relaciona direta ou indiretamente com as questões que envolvem geometria espacial e geometria analítica.

Para fazer o Enem, é de grande importância estudar os principais tópicos da geometria plana, que são:

• ângulos;

• polígonos;

• triângulos;

• quadriláteros;

• círculo e circunferência;

• área e perímetro de figuras planas;

• trigonometria.

Exercícios resolvidos

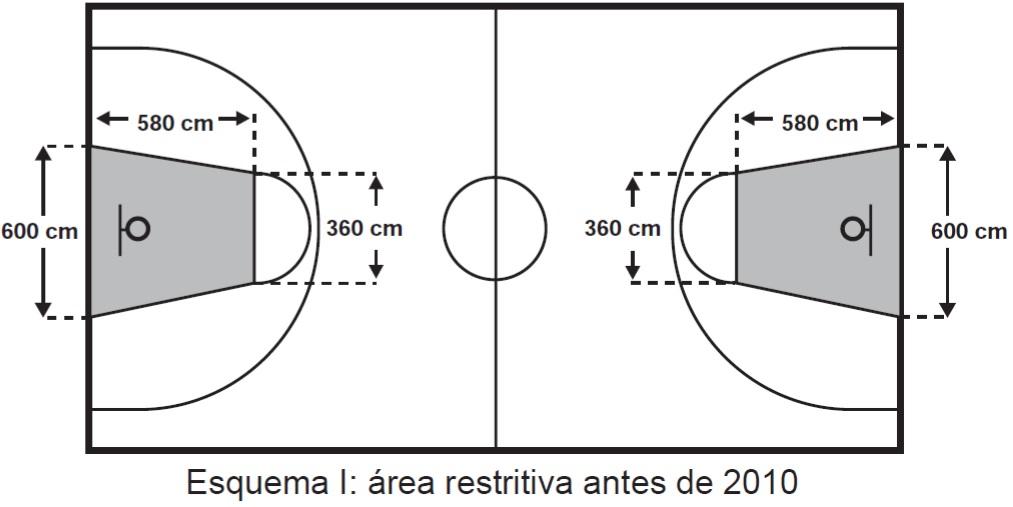
Questão 1 – (Enem 2015) O Esquema I mostra a configuração de uma quadra de basquete. Os trapézios em cinza, chamados de garrafões, correspondem a áreas restritivas.

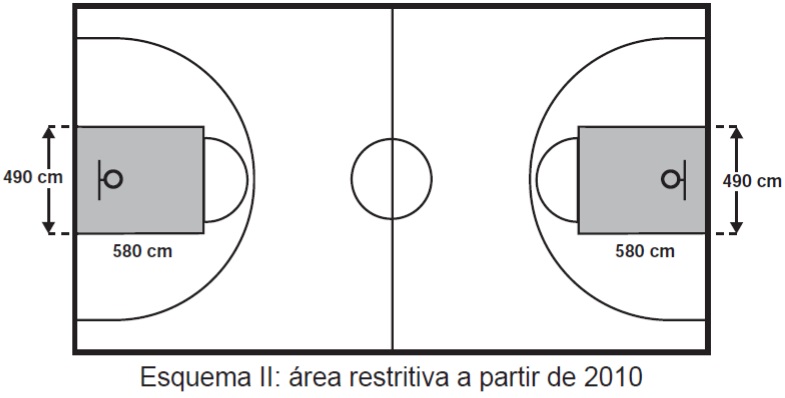
Visando atender as orientações do Comitê Central da Federação Internacional de Basquete (Fiba) em 2010, que unificou as marcações das diversas ligas, foi prevista uma modificação nos garrafões das quadras, que passariam a ser retângulos, como mostra o Esquema II.

Após executadas as modificações previstas, houve uma alteração na área ocupada por cada garrafão, que corresponde a um(a)

A) aumento de 5 800 cm².

B) aumento de 75 400 cm².

C) aumento de 214 600 cm².

D) diminuição de 63 800 cm².

E) diminuição de 272 600 cm².

Resolução

Alternativa A.

1º passo: calcular a área dos garrafões.

No esquema I, o garrafão é um trapézio com bases de 600 cm e 380 cm e altura de 580 cm. A área do trapézio é calculada por:

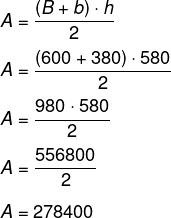
No esquema II, o garrafão é um retângulo de base de 580 cm e altura de 490 cm.

A = b · h

A = 580 · 490

A= 284200

2º passo: calcular a diferença entre as áreas.

284200 – 278400 = 5800 cm²

Questão 2 – (Enem 2019) Em um condomínio, uma área pavimentada, que tem a forma de um círculo com diâmetro medindo 6 m, é cercada por grama. A administração do condomínio deseja ampliar essa área, mantendo seu formato circular, e aumentando, em 8 m, o diâmetro dessa região, mantendo o revestimento da parte já existente. O condomínio dispõe, em estoque, de material suficiente para pavimentar mais 100 m² de área. O síndico do condomínio irá avaliar se esse material disponível será suficiente para pavimentar a região a ser ampliada.

Utilize 3 como aproximação para π.

A conclusão correta a que o síndico deverá chegar, considerando a nova área a ser pavimentada, é a de que o material disponível em estoque

A) será suficiente, pois a área da nova região a ser pavimentada mede 21 m².

B) será suficiente, pois a área da nova região a ser pavimentada mede 24 m².

C) será suficiente, pois a área da nova região a ser pavimentada mede 48 m².

D) não será suficiente, pois a área da nova região a ser pavimentada mede 108 m².

E) não será suficiente, pois a área da nova região a ser pavimentada mede 120 m².

Resolução

Alternativa E.

1º Passo: calcular a diferença entre a área dos dois círculos.

A_{2 –} A₁ = πR² – πr² = π (R² – r² )

r = 6 : 2 = 3
R = 14 : 2 = 7.

π = 3

Então:

A_{2 –} A₁ = 3 (7² – 3² )

A_{2 –} A₁ = 3 (49 – 9)

A_{2 –} A₁ = 3 · 40 = 120