A geometria espacial é a área da matemática que estuda os sólidos geométricos e a geometria no espaço. Pensar na geometria com objetos tridimensionais é buscar compreender o mundo em que vivemos, logo a geometria espacial tem como objetivo entender as formas de objetos em três dimensões.
A geometria plana, que se volta para objetos em duas dimensões, é a base para uma série de conceitos da geometria espacial, sendo essencial o domínio de uma para compreender a outra. A geometria espacial surge a partir de elementos primitivos, que são assim chamados por não possuírem uma definição. São eles: o ponto, a reta, o plano e o espaço.
Tendo como base os elementos primitivos, podemos desenvolver uma série de conceitos importantes e conhecer as formas, como os poliedros e os corpos redondos. Além de conhecer esses sólidos, é importante compreender o cálculo de volume e de área total, pois cada sólido geométrico possui sua fórmula específica.
Leia também: Quais são as dimensões do espaço?

Tópicos deste artigo
- 1 - Conceitos básicos da geometria espacial
- 2 - Figuras da geometria espacial
- 3 - Fórmulas da geometria espacial
- 4 - Diferença entre geometria espacial e geometria plana
- 5 - Exercícios resolvidos
Conceitos básicos da geometria espacial
Os primeiros conceitos que precisamos entender são os elementos primitivos da geometria espacial. Eles não possuem definição, mas conseguimos intuitivamente reconhecê-los. É a partir deles que temos todos os conceitos da geometria. Os elementos primitivos são a reta, o ponto, o plano e o espaço.
As noções de semirreta, segmento de reta e até mesmo a de ângulo surgem a partir desses elementos. Com base neles, também podemos definir conceitos mais avançados, como sólidos geométricos, volume, área total etc.
Então começaremos reconhecendo a representação desses elementos primitivos.
-
Pontos
-
Reta
-
Plano

-
Espaço
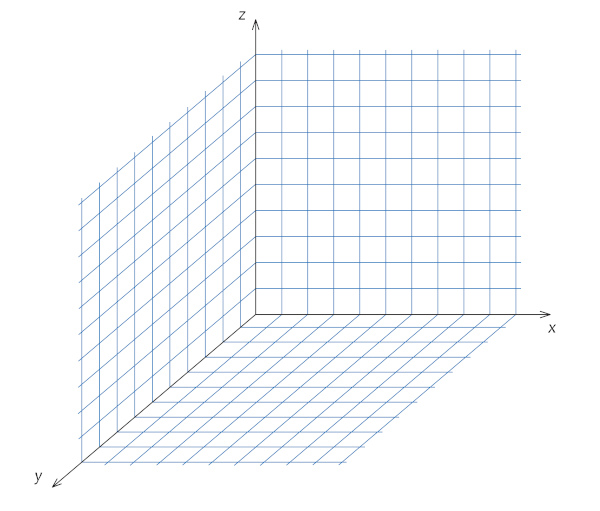
Pensando nos elementos primitivos, o ponto, a reta e o plano são objetos também da geometria plana. Na geometria espacial, estudamos o comportamento desses elementos no espaço, ou seja, em um universo tridimensional.
Veja também: Quais são as possíveis posições relativas entre reta e plano?
Figuras da geometria espacial
Na geometria espacial, são estudados os sólidos geométricos. Os mais estudados são divididos em dois grupos: os poliedros e os corpos redondos.
-
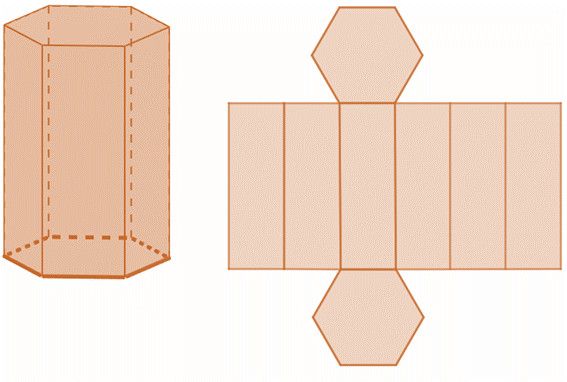
Poliedros
Poliedros são sólidos geométricos compostos com faces formadas por polígonos. Todo poliedro é composto por vértices, faces e arestas.
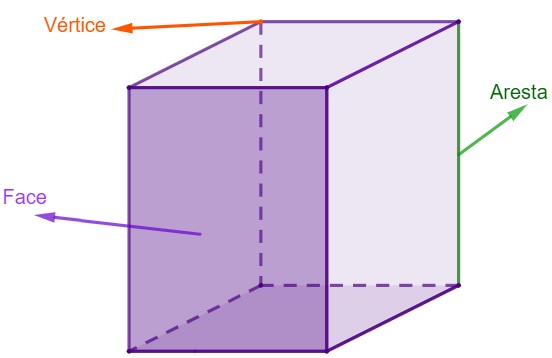
As faces são os polígonos que formam o sólido geométrico — nesse caso, são os retângulos que formam o sólido. As arestas são os segmentos de reta que ligam os vértices do sólido. Podemos notar também que a aresta é o lado do polígono que forma a face do poliedro. Já os vértices são os pontos formados pelo encontro de três ou mais arestas.
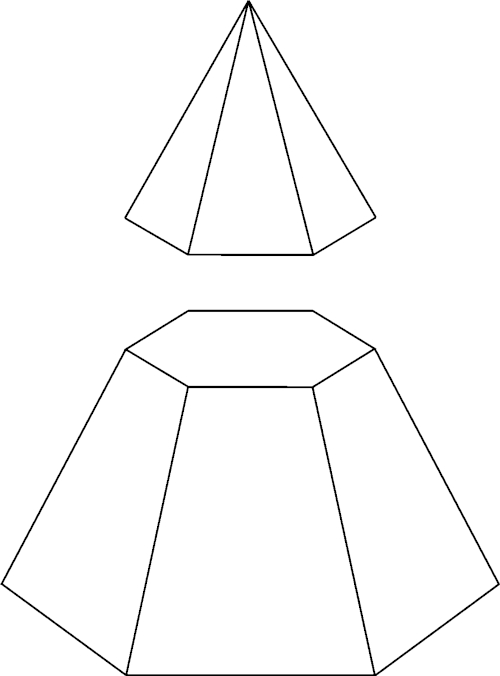
Os principais poliedros são as pirâmides e os prismas. Existem pirâmides de base triangular, quadrada, pentagonal, etc. Já os prismas mais conhecidos são o cubo e o paralelepípedo, mas também há prismas de base triangular, pentagonal, entre outros.
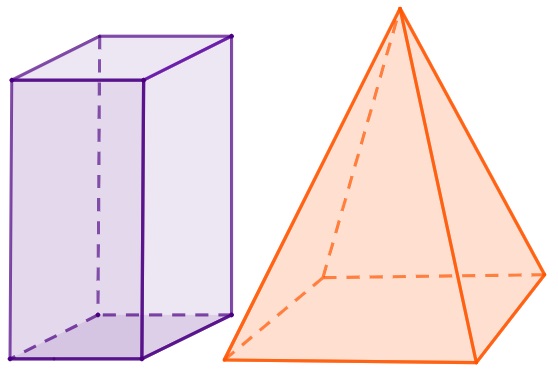
-
Corpos redondos
Os corpos redondos são sólidos geométricos que possuem superfícies curvas, logo não possuem vértice, face e aresta. Conhecidos também como sólidos de revolução, os principais corpos redondos são o cilindro, o cone e a esfera.
Veja também: Projeções ortogonais – imagens de figuras geométricas ou elementos matemáticos projetadas em um plano

Fórmulas da geometria espacial
Todos esses sólidos geométricos possuem fórmulas específicas para o cálculo de volume (V) e da área total (At).
-
Prisma
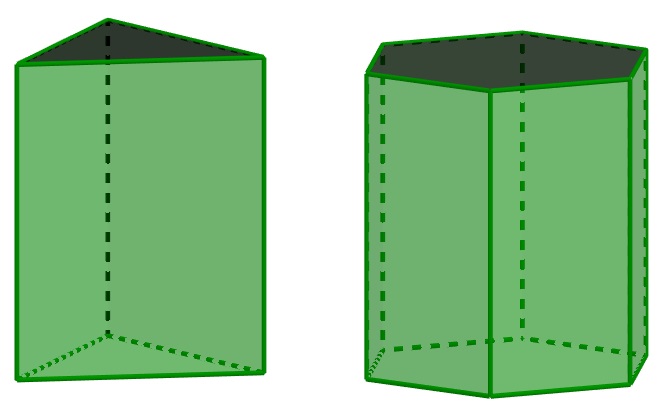
Para os prismas, é possível perceber que a sua área da base pode ser diferente de um formato para o outro, logo a área total e o volume dependem diretamente da área da base.
V = Ab· h
At = 2Ab + Al
Ab → área da base
Al → área lateral
h → altura
-
Pirâmide
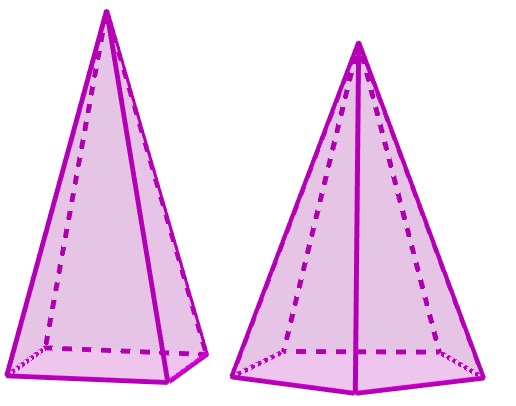
Assim como os prismas, a base da pirâmide pode ser diferente, logo o volume depende diretamente da base.
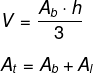
Ab → área da base
Al → área lateral
h → altura
-
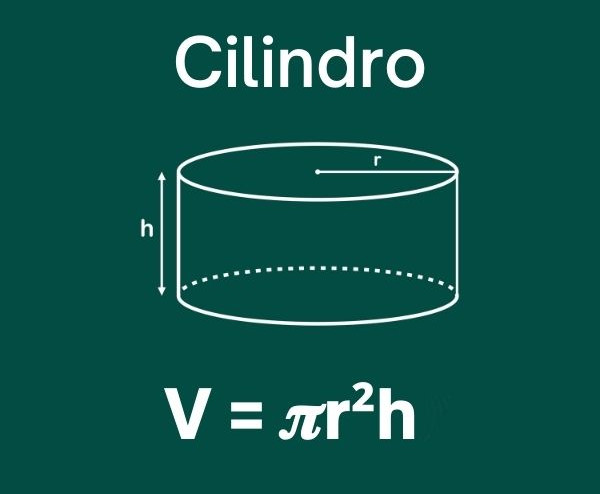
Cilindro

O cilindro sempre possui base circular, logo sua área total e seu volume dependem somente da altura (h) e do raio (r) do cilindro.
V = πr² ·h
At = 2πr ( r + h)
-
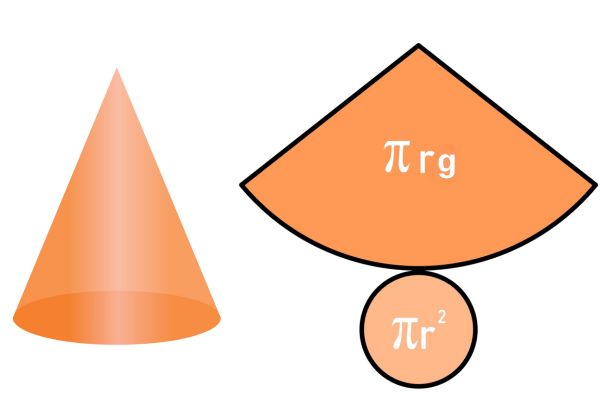
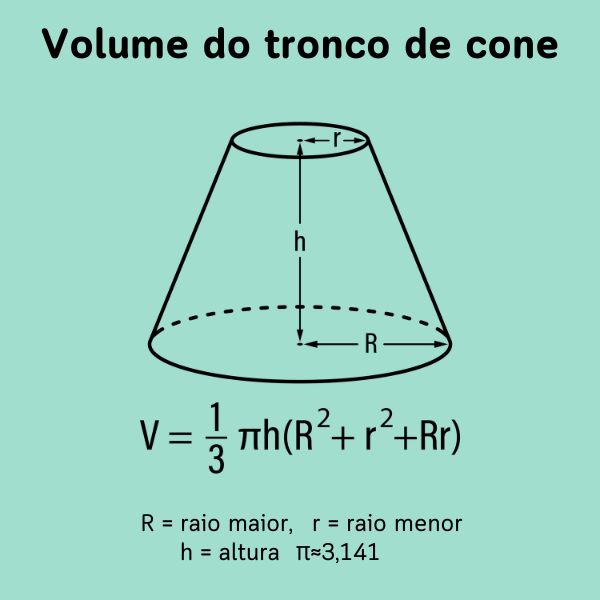
Cone
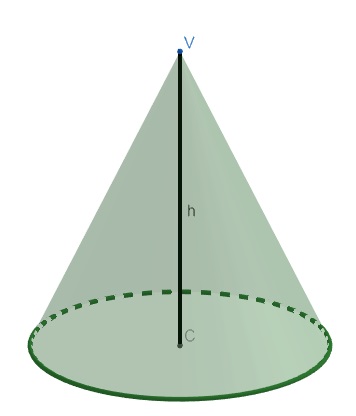
Com base também circular, o volume do cone depende somente da sua altura e de seu raio. Porém, para encontrar a sua área total, é necessário encontrar a geratriz do cone.
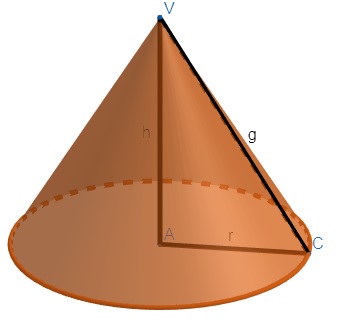
Logo, no cone, há três fórmulas importantes. Uma delas é para encontrar a geratriz (g), e as outras são as já conhecidas dos outros poliedros, isto é, fórmulas de volume e de área total.
![]()
g² = r² + h²
At = πr (r+ g)
-
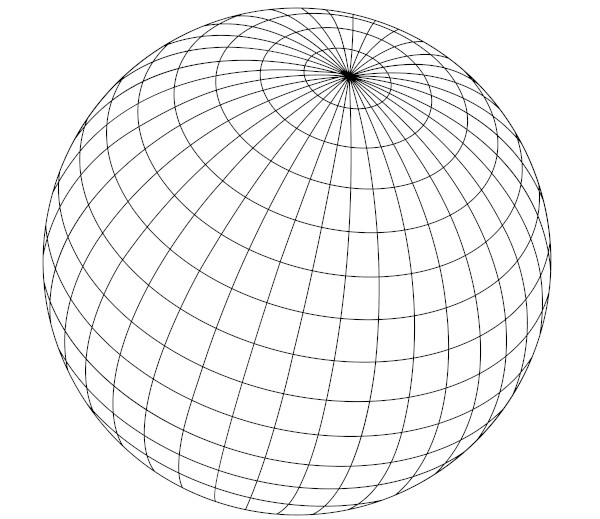
Esfera
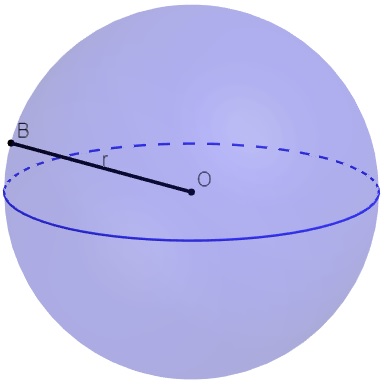
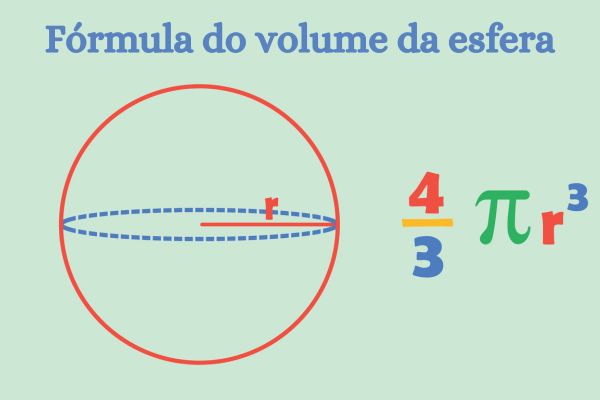
Para calcular o volume e a área total da esfera, é necessário conhecer o valor do raio. As fórmulas são:
![]()
At = 4πr²
Veja também: Temas de matemática que mais caem no Enem
Diferença entre geometria espacial e geometria plana
É importante entender que todos os elementos e estudos realizados na geometria plana servem de base e preparação para o estudo da geometria espacial. Então, não são “mundos” totalmente separados, já que a geometria espacial é uma extensão da geometria plana, que é bidimensional, só que agora pensada em um universo tridimensional.
Para construir a pirâmide, por exemplo, a sua base é formada por um polígono, que é um objeto estudado na geometria plana, e as faces laterais são formadas por triângulos. A junção desses elementos da geometria plana permite a construção de um sólido geométrico, que é estudado na geometria espacial. Logo, ambos estão totalmente ligados. A principal diferença entre a geometria plana e a geometria espacial está na quantidade de dimensões estudadas.

Exercícios resolvidos
Questão 1 – (Enem 2015) Para resolver o problema de abastecimento de água foi decidida, numa reunião do condomínio, a construção de uma nova cisterna. A cisterna atual tem formato cilíndrico, com 3 m de altura e 2 m de diâmetro, e estimou-se que a nova cisterna deverá comportar 81 m³ de água, mantendo o formato cilíndrico e a altura da atual. Após a inauguração da nova cisterna a antiga será desativada. Utilize 3,0 como aproximação para π.
Qual deve ser o aumento, em metros, no raio da cisterna para atingir o volume desejado?
A) 0,5
B) 1,0
C) 2,0
D) 3,5
E) 8,0
Resolução
Alternativa C.
Dados: h = 3, π = 3 e V = 81m³.
O volume do cilindro é calculado por:
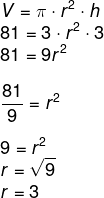
Sabendo que o diâmetro antigo era 2 e como o raio é metade do diâmetro, o raio antigo era igual a 1.
Logo, de 1 para 3, houve um aumento de 2 metros.
Questão 2 – (Enem 2017) Uma rede hoteleira dispõe de cabanas simples na ilha de Gotland, na Suécia, conforme Figura 1. A estrutura de sustentação de cada uma dessas cabanas está representada na Figura 2. A ideia é permitir ao hóspede uma estada livre de tecnologia, mas conectada com a natureza.
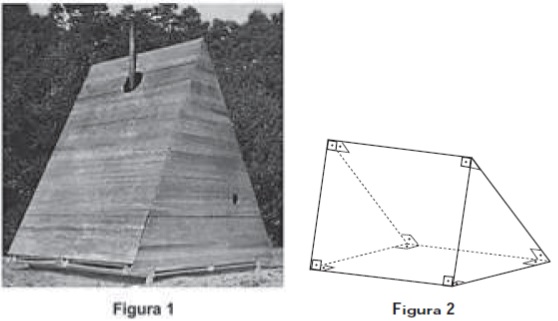
A forma geométrica da superfície cujas arestas estão representadas na figura 2 é:
A) tetraedro.
B) pirâmide retangular.
C) tronco de pirâmide retangular.
D) prisma quadrangular reto.
E) prisma triangular reto.
Resolução
Alternativa E. A figura 2 possui duas bases triangulares e ângulos retos, logo é um prisma triangular reto.