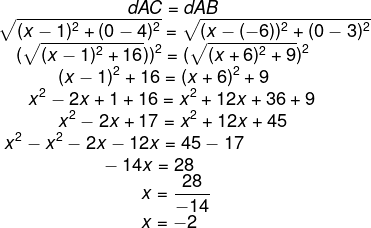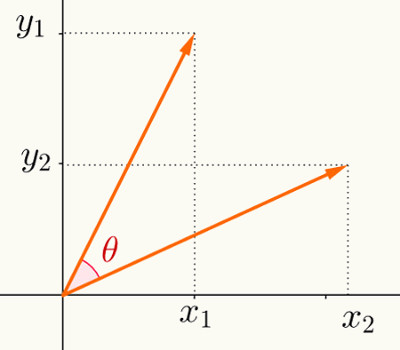Geometria analítica

A geometria analítica é a área da matemática que analisa elementos da geometria em um plano cartesiano. O plano cartesiano é um plano de coordenadas contendo duas retas perpendiculares, nele conseguimos representar elementos da geometria analítica, como pontos, retas, circunferências, entre outros.

Na geometria analítica, há o desenvolvimento de conceitos importantes, tornando possível algebrizar os objetos geométricos e descrevê-los por meio de equações, como a equação da reta e a equação da circunferência, além da existência de algumas fórmulas para encontrar a distância entre dois pontos, o ponto médio de um segmento, entre outros.

Leia também: Como determinar a distância entre um ponto e uma reta?

Tópicos deste artigo

• 1 - O que a geometria analítica estuda?
• 2 - Conceitos da geometria analítica
• 3 - Fórmulas da geometria analítica
  • Distância entre dois pontos
  • Ponto médio
  • Condição de alinhamento
  • Equação da reta
  • Equação da circunferência
• 4 - Exercícios resolvidos

O que a geometria analítica estuda?

A geometria analítica permitiu a junção da geometria com a álgebra, tornando possível o desenvolvimento de muitos conceitos importantes na matemática, como a criação de uma área muito importante da matemática avançada, conhecida como análise.

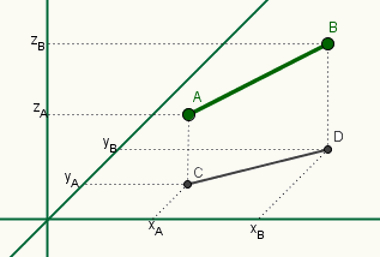
A geometria analítica desenvolve-se em um sistema de coordenadas conhecido como plano cartesiano. Com base no plano cartesiano, é possível representar pontos de forma geométrica e anexá-los a uma coordenada algébrica. Com o avanço dos conceitos, tornou-se possível calcular a distância entre dois pontos localizados no plano cartesiano ou até mesmo desenvolver equações que descrevam o comportamento de retas, circunferências, entre outras figuras da geometria plana.

Vale ressaltar que a geometria analítica que conhecemos é estruturada com base em conceitos da geometria euclidiana, respeitando todas as noções de geometria desenvolvidas no que conhecemos também como geometria plana.

Conceitos da geometria analítica

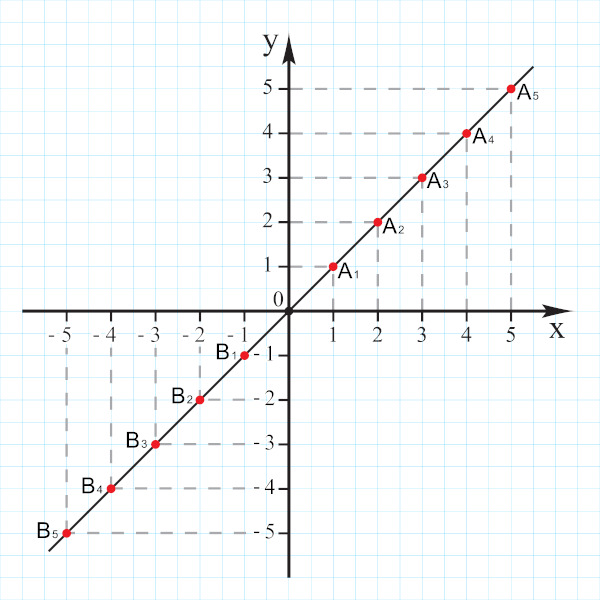
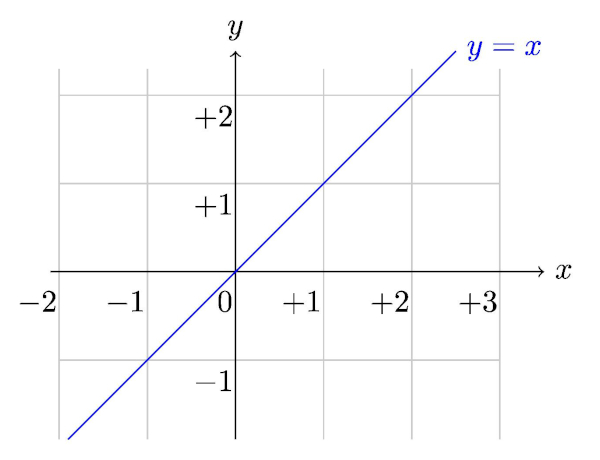
Para compreender a geometria analítica como um todo, é necessário aprender o que é um plano cartesiano. O plano cartesiano é formado por dois eixos perpendiculares entre si, ou seja, que formam um ângulo de 90º. Em cada um desses eixos, representamos uma reta numérica com todos os números reais. O eixo vertical é conhecido como eixo das ordenadas ou também como eixo y. O eixo horizontal é conhecido como eixo das abcissas ou eixo x.

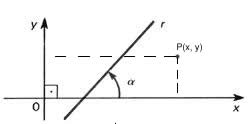
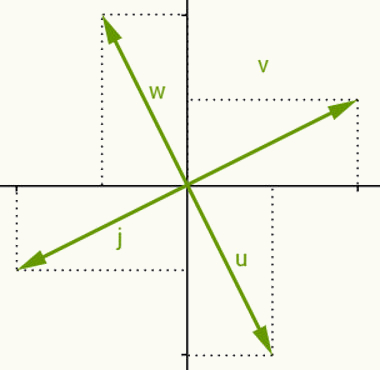
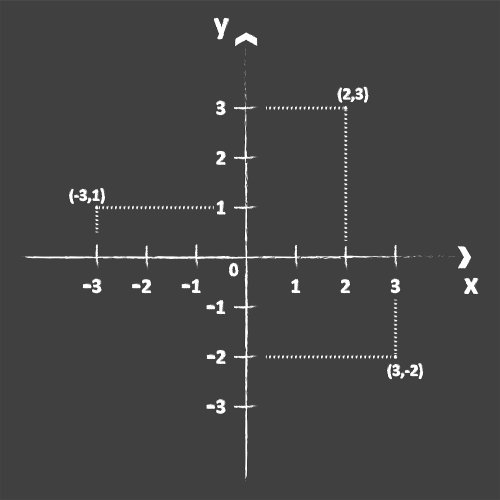
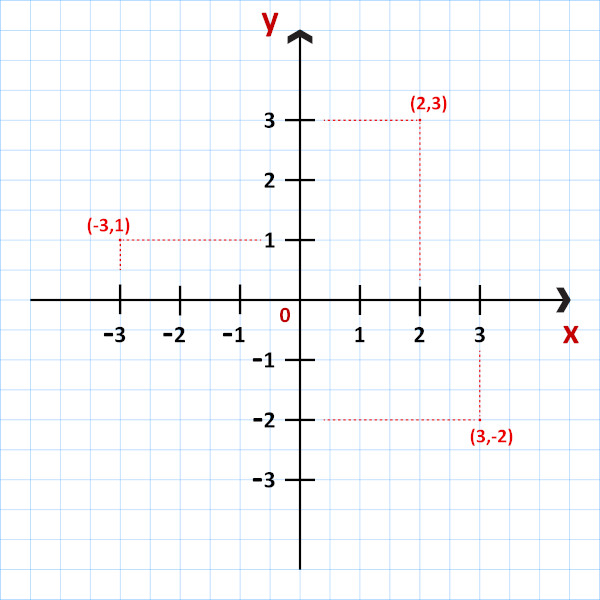
Ao representar qualquer objeto no plano cartesiano, é possível extrair informações algébricas desse objeto, a primeira delas e a mais simples é o ponto. Todo ponto no plano cartesiano pode ser representado por um par ordenado de acordo com a sua localização em relação a cada um dos eixos. Esse par ordenado é representado sempre da seguinte maneira:

De acordo com a posição do elemento geométrico ou de seu comportamento, a geometria analítica foi desenvolvendo meios algébricos de estudar elementos que antes eram somente geométricos. Essas representações algébricas geraram fórmulas importantes para a geometria analítica.

Veja também: Posição de um ponto em relação a uma circunferência

Fórmulas da geometria analítica

• Distância entre dois pontos

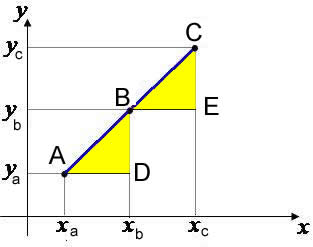
Tendo bem definidos os conceitos básicos (o que é um plano cartesiano e como pontos são representados), passa-se ao entendimento de que a geometria analítica é uma construção de conceitos desenvolvidos ao longo do tempo. O primeiro deles é a distância entre dois pontos, sendo possível calculá-la por meio de uma fórmula.

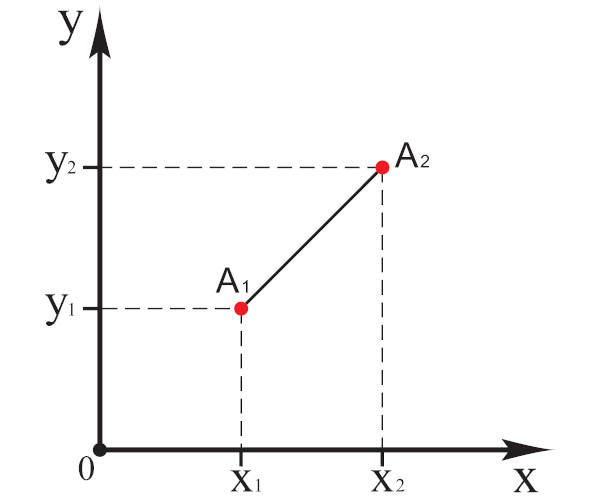
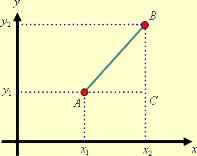
Dados os pontos A₁ e A₂ do plano cartesiano, para calcular da distância entre eles (dA₁A₂), utilizamos a fórmula:

Essa distância nada mais é que o comprimento do segmento que liga os dois pontos.

Exemplo:

Dado A(2,3) e B(5,1), qual é a distância entre esses dois pontos?

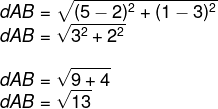
• Ponto médio

Com base na ideia de distância, e do seguimento que une dois pontos, outra fórmula importante é a de ponto médio de um seguimento. Para calcular o ponto M(x_m,y_m), que é ponto médio do seguimento A₁(x₁,y₁) e A₂(x₂,y₂), utilizamos a fórmula:

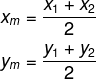
Essa fórmula nada mais é que a média aritmética entre as abcissas dos dois pontos e as ordenadas também dos dois pontos.

Exemplo:

Encontre o ponto médio entre os pontos A(-2,5) e B(6,3).

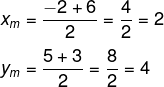
O ponto médio é o ponto M(2,4).

• Condição de alinhamento

A condição de alinhamento de três pontos serve para realizar a verificação de que três pontos — A₁ (x₁,y₁), A₂(x₂,y₂) e A₃(x₃,y₃) — estão alinhados ou não. Calculamos o determinante da seguinte matriz:

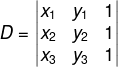
Existem dois casos possíveis, se o determinante for igual a 0, significa que os três pontos estão alinhados, caso contrário, dizemos que os pontos não estão alinhados ou então que são vértices de um triângulo.

Acesse também: Posição relativa entre uma reta e uma circunferência

• Equação da reta

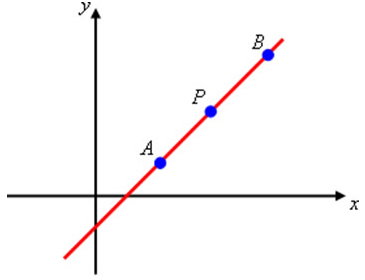
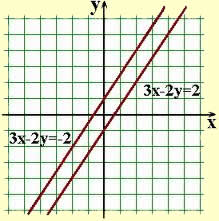
Uma figura geométrica muito estudada na geometria analítica é a reta. Existem duas possibilidades para a sua equação, são elas:

• Equação geral da reta: ax + by + c = 0

• Equação reduzida da reta: y = mx + n

• Equação da circunferência

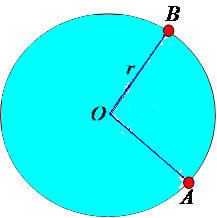
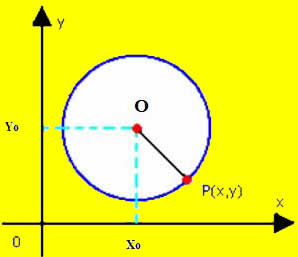
Outras equações estudadas na geometria analática são as equações geral e reduzida da circunferência, tendo o centro definido pelo ponto O(x_c,y_c):

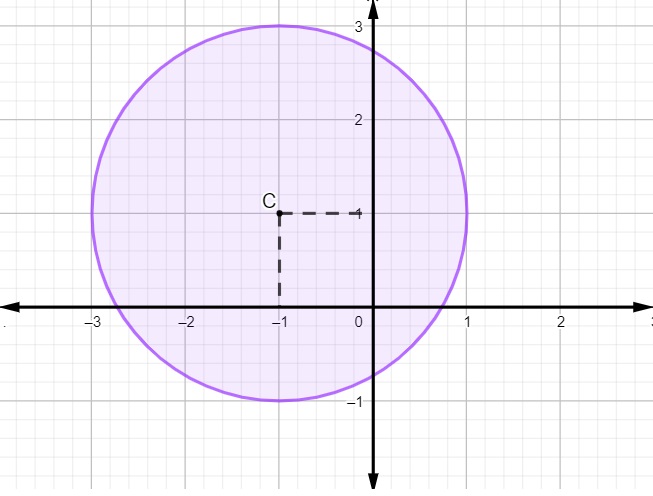
• Equação reduzida da circunferência: (x – x_c)² + (y – y_c)² = r²

• Equação geral da circunferência: x² + y² – 2x_cx – 2ycy + x_c² + y_c² – r² = 0

Existem outras equações menos estudadas, mas, ainda assim, importantes na geometria analítica, são as equações das cônicas.

Exercícios resolvidos

Questão 1 - A economia no consumo de combustível é um fator importante para a escolha de um carro. É considerado mais econômico o carro que percorre a maior distância por litro de combustível.

O gráfico apresenta a distância (km) e o respectivo consumo de gasolina (L) de cinco modelos de carros.

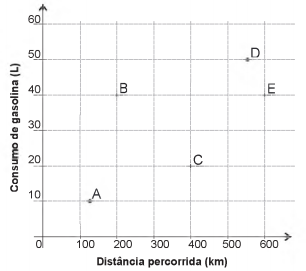
O carro mais econômico em relação ao consumo de combustível é o modelo:

A) A

B) B

C) C

D) D

E) E

Resolução

Alternativa C

Analisando o plano cartesiano, basta realizar as coordenadas de cada um dos pontos, ou seja, cada um dos modelos de carro.

O ponto A tem as coordenadas aproximadamente iguais a A(125,10).

O modelo A percorreu cerca de 125 km com 10 litros. Dividindo 125 : 10 = 12,5 km/L.

O modelo B percorreu 200 km com 40 litros. Dividindo 200 : 40 = 5 km/L.

O modelo C percorreu 400 km com 20 litros. Dividindo 400 : 20 = 20 km/L.

O modelo D percorreu aproximadamente 550 km com 50 litros. Dividindo 550 : 50 = 11 km/L.

O modelo E percorreu 600 km com 40 litros. Dividindo 600 : 40 = 15 km/L.

O modelo C é o mais econômico.

Questão 2 - Se um ponto C com coordenadas (x,0) está a mesma distância dos pontos A(1,4) e B(-6,3), a abscissa de C é igual a:

A) 3

B) 2

C) 1

D) -1

E) -2

Resolução

Alternativa E

Sabendo que as distâncias são iguais, então temos que dAC = dBC.