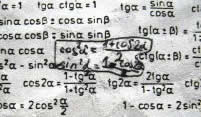A partir das relações trigonométricas no triângulo retângulo, definem-se as funções trigonométricas do seno e cosseno. Em decorrência destas, surge a primeira relação fundamental da Trigonometria:
tg (x) = sen (x)
cos (x)
Essa relação é conhecida como a função trigonométrica da tangente. A segunda e talvez a mais importante das relações fundamentais da trigonometria é:
sen² (x) + cos² (x) = 1
A prova dessas relações pode ser feita a partir de análises de aplicações do teorema de Pitágoras no triângulo retângulo. Entretanto, a demonstração dessas relações fundamentais não é interessante nesse momento.
Ainda dentro das relações fundamentais, temos as funções inversas do seno, do cosseno e da tangente. Cada uma delas recebe um nome especial, que são:
Secante → função inversa do cosseno
sec (x) = 1
cos (x)
Cossecante → função inversa do seno
cossec (x) = 1
sen (x)
Cotangente → função inversa da tangente
cotg (x) = 1 ou cotg (x) = cos (x)
tg (x) sen (x)
Desenvolvendo as relações fundamentais, podemos estabelecer relações decorrentes que também são de grande importância dentro da Trigonometria. Vejamos a demonstração para determiná-las:
1ª relação decorrente:
Considere a relação sen² (x) + cos² (x) = 1. Vejamos o que teremos se dividirmos toda a igualdade por cos² (x).
sen² (x) + cos² (x) = 1
cos² (x) cos² (x) cos² (x)
tg² (x) + 1 = sec² (x)
ou
tg² (x) = sec² (x) – 1
2ª relação decorrente:
Partindo novamente da relação sen² (x) + cos² (x) = 1, vamos agora dividir a igualdade por sen² (x).
sen² (x) + cos² (x) = 1
sen² (x) sen² (x) sen² (x)
1 + cotg² (x) = cossec² (x)
ou
cotg² (x) = cossec² (x) – 1
As funções trigonométricas, as relações fundamentais da trigonometria e as relações decorrentes são de extrema importância nas resoluções de equações e identidades trigonométricas. Junto a elas, são também muito utilizadas as funções do arco duplo:
sen (2x) = 2 . sen (x) . cos (x)
cos (2x) = cos² (x) – sen² (x)
tg (2x) = 2. tg (x)
1 – tg² x
Aproveite pra conferir nossa videoaula sobre o assunto: