Chamamos de função logarítmica a função que possui domínio nos números reais positivos e contradomínio nos números reais, e, além disso, sua lei de formação é f(x) = logax. Existe uma restrição para a base em que “a” do logaritmo precisa ser um número positivo diferente de 1. É bastante comum ver-se aplicações de função logarítmica no comportamento de reações químicas, na matemática financeira, e na medida da magnitude de terremotos.
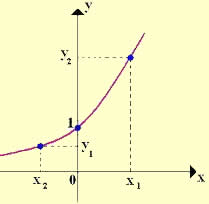
O gráfico dessa função sempre estará no primeiro e quarto quadrantes do plano cartesiano, já que o domínio é o conjunto dos números reais positivos, ou seja, o valor de x nunca será negativo nem zero. Esse gráfico pode ser crescente ou decrescente, a depender do valor da base da função. A função logarítmica comporta-se como inversa da exponencial.
Leia também: Definição e demonstração de domínio, contradomínio e imagem
Tópicos deste artigo
- 1 - O que é função logarítmica?
- 2 - Domínio da função logarítmica
- 3 - Gráfico da função logarítmica
- 4 - Função logarítmica e função exponencial
- 5 - Exercícios resolvidos
O que é função logarítmica?
Uma função é tida como logarítmica quando f: R*+ → R, ou seja, o domínio é o conjunto dos números reais positivos e não nulos e o contradomínio é o conjunto dos números reais, além disso, sua lei de formação é igual a:
f(x) = logax
f(x) → variável dependente
x→ variável independente
a → base do logaritmo
Por definição, em uma função, a base do logaritmo tem que ser um número positivo e diferente de 1.
Exemplos:
a) f(x) = log2x
b) y = log5 x
c) f(x) = logx
d) f(x) = log1/2x
Domínio da função logarítmica
Para que a função seja contínua, por definição, o domínio de uma função logarítmica é o conjunto dos números reais positivos diferentes de zero, isso significa que x sempre será um número positivo, o que faz com que o gráfico da função restrinja-se ao primeiro e segundo quadrantes.
Caso x pudesse admitir um valor negativo (sendo assim o domínio não teria as restrições citadas), encontraríamos situações de indeterminação, pois é impossível que uma base negativa elevada a um número qualquer tenha como resultado um número positivo, o que contraria inclusive a definição de função.
Por exemplo, supondo x = -2, então f(-2) = log2 -2, não havendo valor algum que faça com que 2y = -2. No entanto, na definição de função, para todo elemento no domínio, precisa existir um elemento correspondente no contradomínio. Sendo assim, é importante que o domínio seja R*+ para que se tenha uma função logarítmica.
Veja também: Quais as diferenças entre função e equação?
Gráfico da função logarítmica
Existem duas possibilidades de comportamento para o gráfico de uma função logarítmica, podendo ser crescente ou decrescente. Um gráfico é conhecido como crescente quando à medida que o valor de x aumenta, o valor de f(x) também aumenta, e como decrescente quando à medita que o valor de x aumenta, o valor de f(x) diminui.
Para verificar se a função é crescente ou decrescente, é necessário analisar o valor da base do logaritmo:
Dada a função f(x) = logax
- Se a > 1 → f(x) é crescente. (Quando a base do logaritmo é um número maior que 1, a função é crescente.)
- Se 0 < a < 1 → f(x) é decrescente. (Quando a base do logaritmo é um número entre 0 e 1, então a função é decrescente.)
-
Função crescente
Para construção do gráfico, vamos atribuir valores para x e encontrar o correspondente em y.
Exemplo:
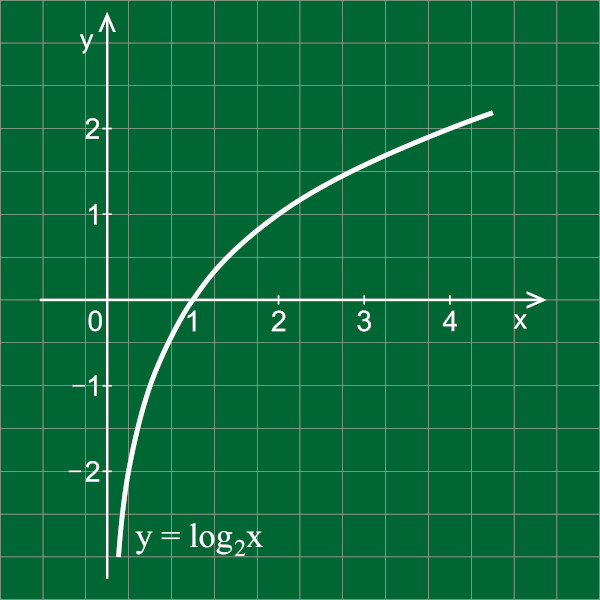
f(x) = log2x

Marcando-se os pontos no plano cartesiano, é possível realizar-se a representação gráfica.
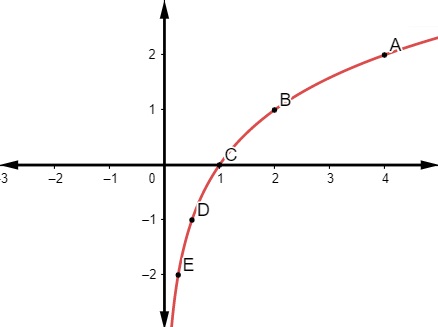
Como a base era maior que 1, então é possível perceber que o gráfico da função comporta-se de forma crescente, ou seja, quanto maior o valor de x, maior será o valor de y.
-
Função decrescente
Para realizar a construção, utilizaremos o mesmo método feito anteriormente.
Exemplo:
![]()
Encontrando alguns valores numéricos na tabela, teremos:

Realizando a marcação dos pares ordenados no plano cartesiano, encontraremos a seguinte curva:
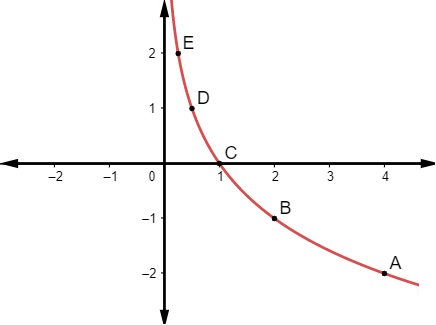
É importante perceber que quanto maior o valor de x, menor será sua imagem y, o que torna esse gráfico decrescente de uma função logarítmica. Isso ocorre porque a base é um número entre 0 e 1.
Acesse também: Funções no Enem: como esse tema é cobrado?
Função logarítmica e função exponencial
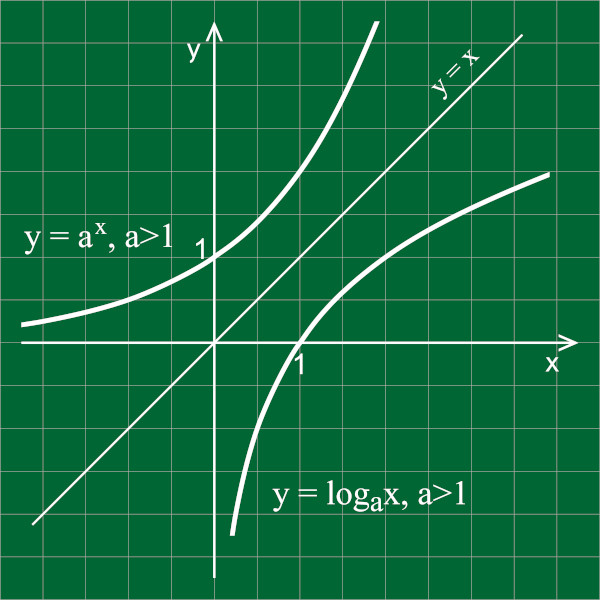
Essa relação é bastante importante para compreender-se o comportamento das funções. Acontece que tanto a função logarítmica quanto a função exponencial são inversíveis, ou seja, admitem inversa, além disso, a função logarítmica é a inversa da função exponencial e vice-versa, veja:
Para encontrar a lei de formação e o domínio e contradomínio da função inversa, precisamos, primeiramente, inverter o domínio e o contradomínio. Se a função logarítmica, como vimos, vai dos R*+ → R, então a função inversa terá domínio e contradomínio R → R*+, além disso, vamos inverter a lei de formação.
y = logax
Para inverter, trocamos x e y de lugar, e isolamos o y, então teremos:
x = logay
Aplicando a exponencial de a dos dois lados, temos que:
ax = alogay
ax = y → função exponencial
Exercícios resolvidos
Questão 1 – (Enem) A Escala e Magnitude de Momento (abreviada como MMS e denotada como MW), introduzida em 1979 por Thomas Haks e Hiroo Kanamori, substituiu a Escala de Richter para medir a magnitude dos terremotos em termos de energia liberada. Menos conhecida pelo público, a MMS é, no entanto, a escala usada para estimar as magnitudes de todos os grandes terremotos da atualidade. Assim como a escala Richter, a MMS é uma escala logarítmica. MW e M0 se relacionam pela fórmula:
![]()
Em que M0 é o momento sísmico (usualmente estimado com base nos registros de movimento da superfície, por meio dos sismogramas), cuja unidade é o dina⋅cm. O terremoto de Kobe, acontecido no dia 17 de janeiro de 1995, foi um dos terremotos que causaram maior impacto no Japão e na comunidade científica internacional. Teve magnitude MW = 7,3.
Mostrando que é possível determinar a medida por meio de conhecimentos matemáticos, qual foi o momento sísmico M0?
A) 10-5,10
B) 10-0,73
C) 1012,00
D) 1021,65
E) 1027,00
Resolução
Alternativa E
Para encontrar o M0, vamos substituir o valor da magnitude dado na questão:
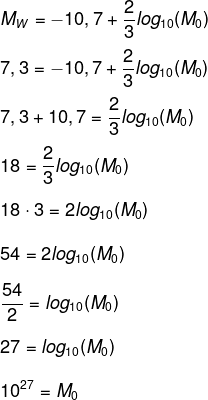
Questão 2 – (Enem 2019 – PPL) Um jardineiro cultiva plantas ornamentais e as coloca à venda quando atingem 30 centímetros de altura. Esse jardineiro estudou o crescimento de suas plantas, em função do tempo, e deduziu uma fórmula que calcula a altura em função do tempo, a partir do momento em que a planta brota do solo até o momento em que ela atinge sua altura máxima, de 40 centímetros. A fórmula é h = 5·log2 (t + 1), em que t é o tempo contado em dia, e h, a altura da planta em centímetro.
A partir do momento em que uma dessas plantas é colocada à venda, em quanto tempo, em dias, ela alcançará sua altura máxima?
A) 63
B) 96
C) 128
D) 192
E) 255
Resolução
Alternativa D
Seja:
t1 o tempo que a planta leva para atingir h1 = 30 cm
t2 o tempo que a planta leva para atingir h2 = 40 cm
Queremos encontrar o intervalo de tempo entre h1 = 30 cm e h2 = 40 cm. Para isso, vamos substituir cada um deles na lei de formação, e fazer a diferença entre t2 e t1.
Encontrando t1:
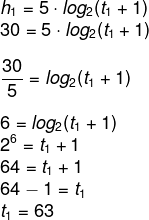
Agora vamos encontrar o valor de t2:
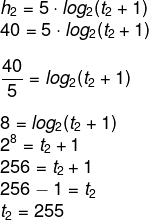
O tempo t é a diferença t2 – t1 = 255 – 63 = 194.