Função linear

A função linear é um caso particular de função do 1º grau ou função afim. Uma função afim é classificada como função linear caso ela possua lei de formação igual a f(x) = ax. Note, então, que para que a função afim seja uma função linear, o valor de b = 0.

O gráfico da função linear sempre passará pela origem do plano cartesiano e pode ser crescente ou decrescente, seguindo a mesma regra da função afim, ou seja:

• se a > 0, então f(x) é crescente;

• se a < 0, então f(x) é decrescente.

Leia também: Funções no Enem — como esse tema é cobrado?

Tópicos deste artigo

• 1 - Resumo sobre função linear
• 2 - Videoaula sobre função linear
• 3 - O que é uma função linear?
• 4 - Valor numérico da função linear
• 5 - Gráfico da função linear
• 6 - Função linear crescente
• 7 - Função linear decrescente
• 8 - Exercícios resolvidos sobre função linear

Resumo sobre função linear

• A função linear é um caso particular de função do 1º grau.

• É uma função do 1º grau em que b = 0.

• Possui lei de formação f(x) = ax.

• O gráfico da função linear sempre passará pela origem 0 (0, 0).

Videoaula sobre função linear

O que é uma função linear?

Quando há uma função afim, isto é, uma função do 1º grau com lei de formação do tipo f(x) = ax + b, sendo o valor de b = 0, a função recebe um nome especial: função linear. Logo, definimos como linear a função do 1º grau em que a lei de formação é f(x) = ax, sendo a um número real qualquer, diferente de 0.

Exemplos:

• f(x) = 2x → função linear com a = 2.

• f(x) = – 0,5x → função linear com a = – 0,5.

• f(x) = x → função linear com a = 1.

• f(x) = – 3x → função linear com a = – 3.

• f(x) = 5x → função linear com a = 5.

Valor numérico da função linear

Em uma função, conhecemos como valor numérico da função o valor encontrado quando substituímos x por um número real.

Exemplos:

Dada a função f(x) = 2x, calcule seu valor numérico quando:

a) x = 3

Para calcular, basta substituir o valor de x na lei de formação:

f(3) = 2 · 3 = 6

b) x = – 0,5

f(– 0,5) = 2 · (– 0,5) = – 1.

Veja também: Quais as diferenças entre função e equação?

Gráfico da função linear

O gráfico de uma função linear, assim como o de uma função afim, é sempre uma reta. Porém, seu gráfico sempre passa pela origem do plano cartesiano, ou seja, pelo ponto 0 (0,0).

O gráfico da função linear pode ser crescente ou decrescente, dependendo do valor do seu coeficiente angular, ou seja, do valor de a. Dessa forma,

• caso a seja um número positivo, ou seja, a > 0, o gráfico da função será crescente;

• caso a seja um número negativo, ou seja, a < 0, então o gráfico da função será decrescente.

Função linear crescente

Para classificar uma função linear como crescente ou decrescente, basta verificar o valor do coeficiente angular a, como já salientado. Isso significa que à medida que o valor de x aumenta, o valor de f(x) também aumenta.

Exemplo:

Vejamos, a seguir, a representação do gráfico da função f(x) = x.

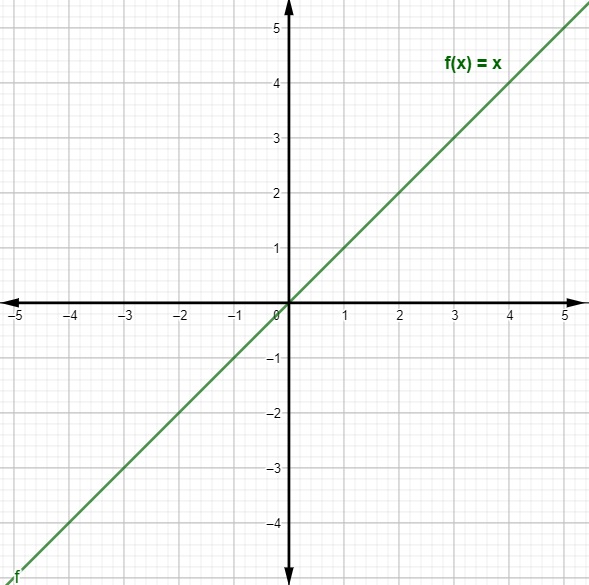
Note que a função linear f(x) = x possui um gráfico crescente, pois sabemos que a = 1; logo, a > 0. Portanto, podemos dizer que a função f(x) = x é uma função linear crescente.

Função linear decrescente

A função linear é considerada decrescente no caso em que à medida que o valor de x aumenta, o valor de f(x) diminui. Para saber se uma função linear é uma função decrescente, basta avaliar o coeficiente angular. Caso ele seja negativo, ou seja, a < 0, então a função será decrescente.

Exemplo:

Temos a representação do gráfico da função f(x) = – 2x:

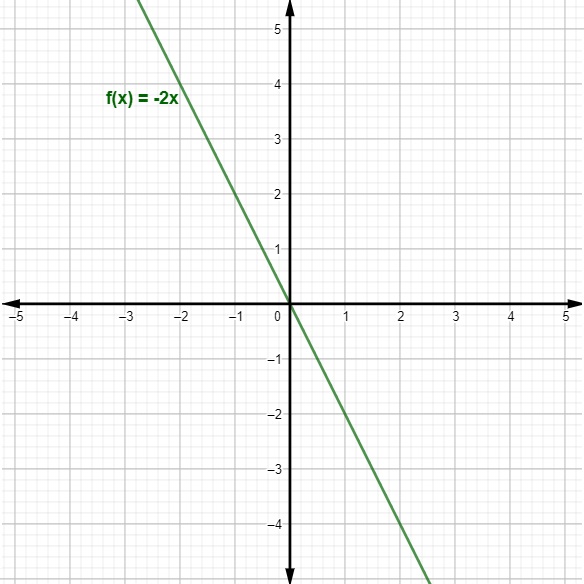
Perceba que o gráfico da função f(x) = – 2x é decrescente. Isso ocorre porque a = – 2, ou seja, a < 0.

Leia também: Estudo do sinal da função afim

Exercícios resolvidos sobre função linear

Questão 1

Analise a função f(x) = 0,3x e julgue as afirmativas a seguir:

I → Essa função é uma função linear.

II → Essa função é decrescente, pois a < 1.

III → f(10) = 3.

Marque a alternativa correta:

A) Somente a afirmativa I é verdadeira.

B) Somente a afirmativa II é verdadeira.

C) Somente a afirmativa III é verdadeira.

D) Somente a afirmativa II é falsa.

E) Somente a afirmativa I é falsa.

Resolução:

Alternativa D

I → Essa função é uma função linear. — verdadeira

Note que b = 0, logo a função é do tipo f(x) = ax, o que faz com que ela seja uma função linear.

II → Essa função é decrescente, pois a < 1. — falsa

Para que a função seja decrescente, a tem que ser menor que 0.

III → f(10) = 3. — verdadeira

f(10) = 0,3 · 10

f(10) = 3

Questão 2

(Fuvest) A função que representa o valor a ser pago após um desconto de 3% sobre o valor x de uma mercadoria é:

A) f(x) = x – 3

B) f(x) = 0,97x

C) f(x) = 1,3x

D) f(x) = – 3x

E) f(x) = 1,03x

Resolução:

Alternativa B

Como será dado um desconto de 3%, o valor da mercadoria será igual a 97% do valor integral. Sabemos que 97% = 0,97, então a função que representa o valor pago é:

f(x) = 0,97x