Função inversa

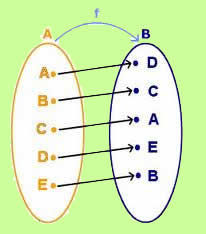
Dada uma função f: A → B, em que f(a) = b, conhecemos como função inversa de f a função f ^-1:B → A, em que f(b) = a. Utilizamos as funções para modelar matematicamente diversas situações do nosso cotidiano, e, em algumas situações, torna-se necessário encontrar a função inversa.

Nem sempre uma função possui inversa, pois a função inversa só existe se a função for bijetora, ou seja, injetora e sobrejetora ao mesmo tempo. Dada uma função que admita inversa, para encontrá-la basta inverter o domínio e o contradomínio e manipular a lei de formação para que ela faça o inverso do que a função fazia. Por exemplo, se uma função pega valores do domínio e soma 5, a função inversa pegará os valores do contradomínio e subtrairá 5.

Veja também: Quais as diferenças entre função e equação?

Tópicos deste artigo

• 1 - Quando uma função admite inversa?
• 2 - Determinação da função inversa
• 3 - Lei de formação da função inversa
• 4 - Gráfico da função inversa
• 5 - Exercícios resolvidos

Quando uma função admite inversa?

Para encontrar uma função inversa, antes é importante saber as condições necessárias para que ela exista. Para encontrá-la, ela precisa ser bijetora. Uma função é chamada de bijetora quando ela é injetora e sobrejetora ao mesmo tempo.

A função é injetora se, dados quaisquer dois elementos distintos do domínio, as imagens desses elementos forem diferentes, ou seja, dados a₁ e a₂ elementos do domínio da função, se a₁ ≠ a₂, então, f(a₁) ≠ f(a₂).

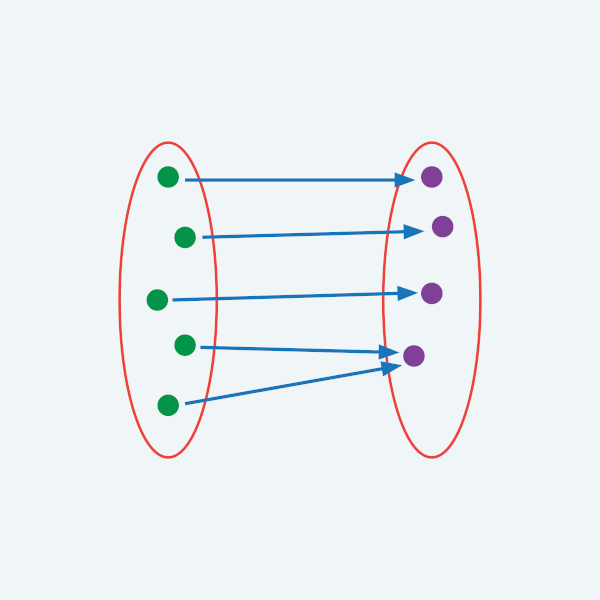
A função é sobrejetora quando o conjunto imagem for igual ao contradomínio da função, isso quer dizer que, para todo elemento b do contradomínio, existirá o elemento a do domínio tal que f(a) = b.

Se a função for injetora e sobrejetora, ela é bijetora e, consequentemente, admite inversa.

Exemplos:

• Dada f: R → R, com a lei de formação f(x) = x+ 1, a função admite inversa, pois se x₁ ≠ x₂, então, f(x₁) ≠ f(x₂), e também, para todo valor no contradomínio, existe um correspondente no domínio, pois, para qualquer número real, existe um antecessor. Dessa forma, se n pertence ao contradomínio, sempre existirá o número n – 1, tal que f(n – 1) = n. Como a função é bijetora, é também inversível.

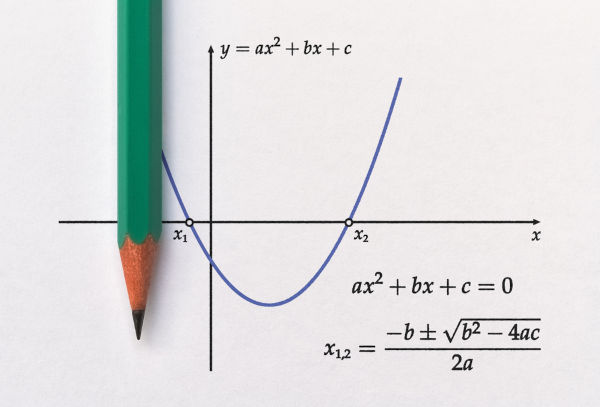
• A função f: R → R, com lei de formação f(x) = x², não é inversível, já que não é bijetora, pois, para f(x) e f(-x), o valor da função é o mesmo, por exemplo: f(-2) = f(2) = 4, logo, f não é injetora e, como consequência, não é inversível.

Leia também: Funções no Enem: como esse tema é cobrado?

Determinação da função inversa

De modo geral, dados dois conjuntos, A e B, consideramos a função f: A → B. Seja A = {a₁, a₂, a₃, a₄} e B = {b₁, b₂, b₃, b₄}, f: é uma função que pega os elementos a_n e leva ao seu correspondente b_n, conforme o diagrama a seguir:

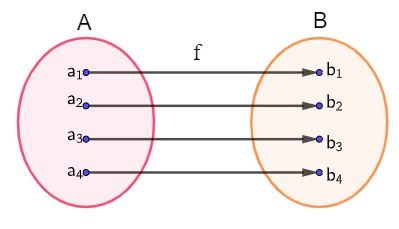
É possível perceber que a função f é bijetora, pois todos os elementos do contradomínio possuem um correspondente no domínio, e esse correspondente é único. A função inversa da função f será:

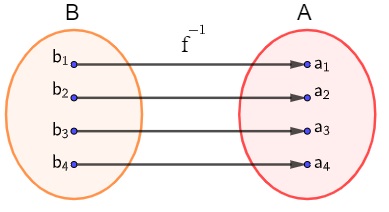
Lei de formação da função inversa

Dada uma função inversível, ou seja, que admite inversa, para encontrar a lei de formação da função inversa, basta trocar a variável x por y e isolar a variável y.

Exemplo 1:

Considere f: R → R, com lei de formação f(x) = 2x + 4, encontre a lei de formação de f ^-1.

Para encontrar a função inversa, sabemos que f(x) = y, ou seja, y = 2x + 1. Faremos a inversão das variáveis, trocaremos x por y e y por x, encontrando a equação a seguir:

x = 2y + 4

Invertendo a igualdade, temos que:

2y + 4 = x

Por fim, isolaremos a variável y.

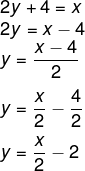
Exemplo 2:

Seja a função f: R⁺ → R⁺, cuja lei de formação é f(x) = x², encontre a sua função inversa.

Note que, nesse caso, o domínio é os números reais positivos e o zero, e o contradomínio também. Quando restringimos a função f(x) = x² a esse domínio e contradomínio, ela é inversível.

Então, dada a equação y = x², vamos inverter as variáveis.

x = y²

y² = x

y = ±√x

Como sabemos, o domínio e o contradomínio são os números positivos e o zero, assim, a lei de formação da função será:

y = +√x

y = √x

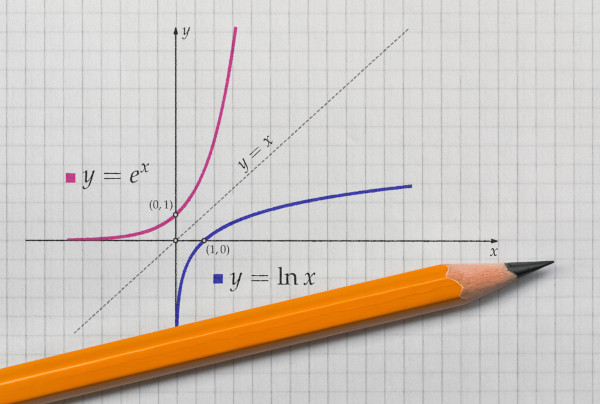
Gráfico da função inversa

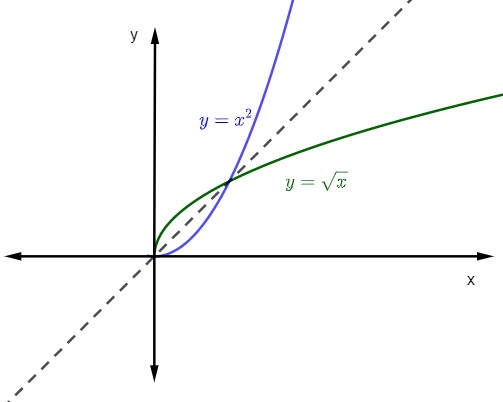
Quando representamos o gráfico de uma função e a sua função inversa no plano cartesiano, os gráficos sempre serão simétricos. Vejamos a representação das funções citadas com domínio e contradomínio nos reais positivos.

Veja também: Dicas de Matemática para o Enem

Exercícios resolvidos

Questão 1 - Dada uma função f: A → B, em que é f(x) = x – 2, onde A {0, 1, 2, 3} e B = {-2, -1, 0, 1, 2}, é correto afirmar que:

A) A função é inversível, pois ela é bijetora.

B) A função é inversível, pois ela é injetora.

C) A função não é inversível, pois ela não é sobrejetora.

D) A função não é inversível, pois ela não é sobrejetora nem injetora.

E) A função não é inversível, pois ela é bijetora.

Resolução

Alternativa C

Primeiro vamos verificar se a função é sobrejetora para o intervalo determinado na questão.

Para que a função seja sobrejetora, todos os elementos de B precisam ter um correspondente em A, para isso, vamos calcular cada um de seus valores numéricos.

f(0) = 0 – 2 = -2

f(1) = 1 – 2 = -1

f(2) = 2 – 2 = 0

f(3) = 3 – 2 = 1

Analisando o conjunto B {-2, -1, 0, 1, 2}, note que existe um elemento no conjunto B que não possui imagem de nenhum elemento no conjunto A, o que faz com que a função não seja sobrejetora. Como ela não é sobrejetora, ela não é bijetora, logo, ela não é inversível.

Resta verificar se ela é injetora.

Analisando os valores encontrados para f(0), f(1), f(2), f(3), podemos perceber que a imagem é sempre diferente, então, a função é injetora.

Dessa forma, ela não é inversível por não ser sobrejetora.

Questão 2 - Seja f(x) uma função inversível, a função inversa de f(x) = 2^x é:

A) y = log_x2

B) y = log₂x

C) y = x²

D) y = √x

E) y = -2^x

Resolução

Alternativa B

y = 2^x

Trocando x por y:

x = 2^y

Agora aplicaremos log₂ nos dois lados:

log₂ x = log₂2^y

log₂ x = ylog₂2

log₂ x = y · 1

log₂ x = y

y = log₂ x