Função do 2º grau

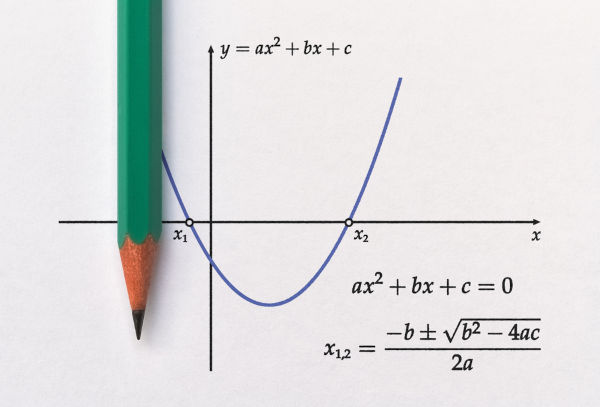
A função do 2º grau é conhecida também como função quadrática ou função polinomial do 2º grau. A função do 2º grau é a função de \(f: \mathbb{R} \to \mathbb{R} \) que tem como lei de formação a expressão f(x) = ax² + bx + c, com a ≠ 0, sendo a, b e c números reais. Podemos representar o gráfico da função de 2º grau no plano cartesiano, e esse gráfico gera uma imagem conhecida como parábola. A parábola pode ser côncava para cima ou para baixo, dependendo do valor de a, e o vértice da parábola é o ponto mínimo quando a parábola tem concavidade para cima ou o ponto máximo quando a parábola tem concavidade para baixo. Outros pontos importantes da parábola são as raízes. A função do 2º grau pode ter 2 raízes, que são os valores de x quando f(x) = 0; graficamente são os pontos em que a parábola corta o eixo x.

Leia também: O que é uma função do 1º grau?

Tópicos deste artigo

• 1 - Resumo sobre a função do 2º grau
• 2 - O que é uma função do 2º grau?
• 3 - Como calcular o valor numérico da função do 2º grau?
• 4 - Raízes da função do 2º grau
• 5 - Gráfico da função de 2º grau
  • → Vértice da parábola
• 6 - Como construir um gráfico da função do 2º grau?
• 7 - Exercícios resolvidos sobre função do 2º grau

Resumo sobre a função do 2º grau

• A função do 2º grau é conhecida também como função quadrática ou função polinomial do 2º grau.
• A função é do 2º grau quando ela é uma função \(f: \mathbb{R} \to \mathbb{R} \) com lei de formação é f(x) = ax² + bx + c, sendo a, b, c \(\in \mathbb{R} \), e a ≠0.
• As raízes, ou zeros da função quadrática, são os valores de x que fazem com que f(x)=0.
• A função do 2º grau pode ter até 2 raízes.
• Para calcular o vértice da parábola e para calcular as raízes da função do 2º grau, existem fórmulas específicas.
• O gráfico da função do 2º grau é conhecido como parábola.
• A parábola pode ter concavidade para cima se a > 0 ou para baixo se a < 0.
• O vértice da função do 2º grau é o valor máximo ou mínimo da função.
• A função de 2º grau possui valor mínimo se sua concavidade for para cima e máximo se sua concavidade for para baixo.

O que é uma função do 2º grau?

Também conhecida como função quadrática, ou função polinomial do 2º grau, a função do 2º grau é a função que possui domínio e contradomínio no conjunto dos números reais, ou seja, \(f: \mathbb{R} \to \mathbb{R} \) com lei de formação f(x) = ax² + bx + c, sendo a, b e c \(\in \mathbb{R} \) e a ≠ 0. Vamos ver alguns exemplos a seguir:

Exemplos:

• \(f(x) = 2x^2 + 3x - 15\)
• \(f(x) = x^2 + 2\)
• \(f(x) = 3x^3 - 5x\)
• \(f(x)= \frac{x^2}{3}+ 2x + 3\)

Todos os exemplos acima são exemplos de função quadrática, e na função quadrática é importante sabermos identificar cada um dos seus coeficientes, ou seja, o valor de a, b e c.

• y = 2x² + 3x - 15

a = 2, b = 3 e c = - 15

• y = x² + 2

a = 1, b = 0 e c = 2

• y = 3x³ - 5x

a = 3  b  = - 5 e c = 0

• \(y= \frac{x^2}{3}+ 2x + 3\)

\(a=\frac{1}{3} , b = 2\ e\ c = 3 \)

Importante: Independentemente da ordem, a é sempre o termo que acompanha x², b é o termo que acompanha x e c é o termo independente. Exemplo:

• y = 2x² - 3x + 5
• y = – 3x + 5 + 2x²

Os exemplos representam a mesma função, somente a ordem dos termos é que está diferente, mas em ambas temos que: a = 2, b = - 3 e c = 5.

Como calcular o valor numérico da função do 2º grau?

Para calcular o valor numérico da função do 2º grau, substituímos o valor de x em sua lei de formação, realizamos os cálculos necessários, que dependem da lei de formação, e encontramos o valor de y, que é o mesmo que o valor de f(x), como nos exemplos a seguir:

Exemplo 1:

Dada a função de lei de formação f(x) = x² - 3x + 4, encontre o valor numérico da função quando:

• x = 1

\(f(1)=12 - 3 \cdot 1 + 4\)

\(f(1)=1 - 3 + 4\)

\(f(1)=-2+4\)

\(f(1)=2\)

Então, quando x = 1, y = 2.

• x = - 2

\(f(-2)=(-2)^2-3 \cdot (-2) +4\)

\(f(-2)=4+6+4\)

\(f(-2)=10+4\)

\(f(-2)=14\)

Então, quando x = - 2, y = 14.

Exemplo 2:

Dada a função de lei de formação f(x) = 2x² - 8, encontre o valor numérico da função quando:

• x = 2

\(f(2)=2\cdot 2^2-8\)

\(f(2)=2\cdot 4-8\)

\(f(2)=8-8\)

\(f(2)=0\)

Se x = 2, y = 0.

• x = - 5

\(f(-5)=2\cdot (5^2)-8\)

\(f(-5)=2\cdot 25-8\)

\(f(-5)=50-8\)

\(f(-5)=42\)

Se x = - 5, y = 42.

Raízes da função do 2º grau

Também chamada de zero da função, a raiz da função do 2º grau é o valor de x que faz com que f(x) = 0. A função do 2º grau pode ter duas raízes, uma raiz ou nenhuma. Para encontrar as raízes de uma função do 2º grau devemos igualar a lei de formação a 0 e calcular as raízes da função utilizando a fórmula de Bhaskara.

Exemplo 1:

Dada a função f(x) = 2x² - 5x + 3, temos que 1 é raiz dessa função, pois:

\(f(1)=2\cdot 1^2-5⋅1+3\)

\(f(1)=2-5+3\)

\(f(1)=-3+3\)

\(f(1)=0\)

Exemplo 2:

Encontre as raízes da função do 2º grau f(x)=x² - 4x - 5.

Resolução:

Primeiro encontraremos a, b e c e calcularemos o valor de Δ.

a = 1, b = - 4 e c = - 5

\(\Delta = b^2 - 4ac\)

\(\Delta = (-4)^2 - 4\cdot 1 \cdot (-5)\)

\(\Delta = 16+20\)

\(\Delta = 36\)

Conhecendo o valor de delta, vamos aplicar a fórmula de Bhaskara:

\(x = {-b\ \pm\ \sqrt{\Delta} \over 2a}\)

\(x = {-(-4)\ \pm\ \sqrt{36} \over 2\ \cdot\ 1}\)

\(x =\frac {4\ \pm\ 6} {2}\)

\(x_1 =\frac {4 + 6} {2} = \frac {10} {2} = 5\)

\(x_2 =\frac {4 - 6} {2} = \frac {-2} {2} = -1\)

Então, as raízes dessa função são x = 5 ou x = -1.

Importante: O valor do delta nos permite saber quantas raízes a função do 2º grau possui.

• Se Δ > 0 → a função possui duas raízes reais distintas.
• Se Δ = 0 → a função possui uma única raiz real.
• Se Δ < 0 → a função não possui raiz real.

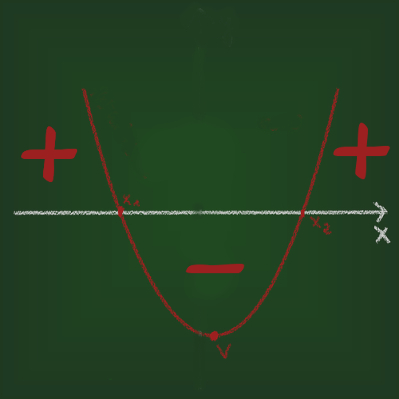
Gráfico da função de 2º grau

O gráfico de uma função do 2º grau possui o formato conhecido como parábola. Essa parábola pode ter concavidade para cima ou para baixo, dependendo do valor do coeficiente a.

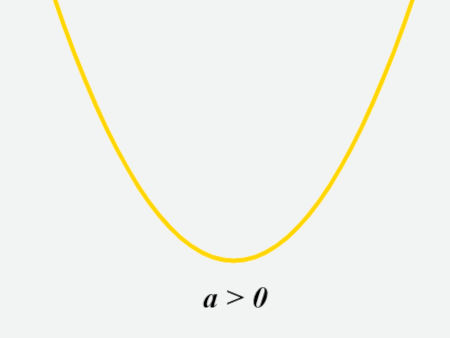
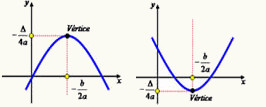
Quando a for positivo a parábola possui concavidade para cima. O vértice da parábola nesse caso é o ponto mínimo da parábola.

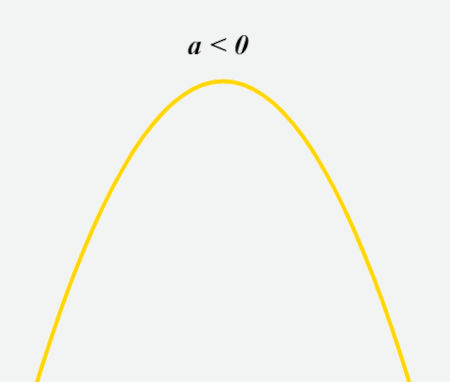
Quando a for negativo, a concavidade da parábola será para baixo. O vértice nesse caso é o ponto máximo da parábola.

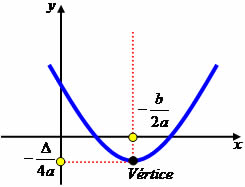
→ Vértice da parábola

O vértice da parábola é o ponto mínimo ou máximo do gráfico da função do 2º grau. Para encontrar as coordenadas de x e y do vértice, utilizamos uma fórmula específica.

\(x_v=\frac{-b}{2a}\)

\(y_v=\frac{-Δ}{4a}\)

Exemplo:

Encontre o vértice da função de 2º grau y = x² - 4x - 5.

Resolução:

Nessa função, temos que a = 1, b = - 4 e c = - 5.

Então:

\(x_v=\frac{-b}{2a}=\frac{-(-4)}{2\ \cdot\ 1}=\frac{4}{2}=2\)

Calculando o delta, sabemos que:

\(Δ=b^2-4ac\)

\(\Delta = (-4)^2 -4\cdot 1 \cdot (-5)\)

\(\Delta = 16+20\)

\(\Delta = 36\)

Então:

\(y_v=\frac{-Δ}{4a}=\frac{-36}{4\ \cdot\ 1}=\frac{-36}{4}=-9\)

Logo, o vértice da função é o ponto V(2, -9).

Como construir um gráfico da função do 2º grau?

Para construir o gráfico da função do 2º grau, precisamos calcular os zeros da função, encontrar a coordenada do seu vértice e verificar em qual ponto o gráfico da função toca o eixo y.

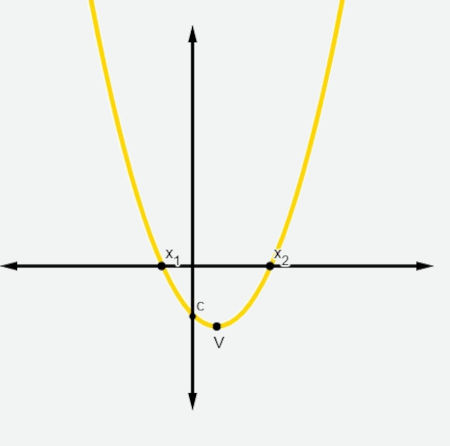
Os pontos x₁ e x₂ são as raízes da função, o ponto V é o seu vértice e o ponto c é o ponto em que a parábola toca o eixo y.

Exemplo:

Represente o gráfico da função f(x) = x² - 4x + 3.

Resolução:

Primeiro vamos calcular os zeros dessa função:

x² - 4x + 3 = 0

a = 1, b = - 4  e c = 3

Então temos que:

\(\Delta = b^2 - 4ac\)

\(\Delta = (-4)^2 - 4\cdot 1\cdot 3 \)

\(\Delta = 16-12\)

\(\Delta = 4\)

Calculando o valor de Δ, agora vamos substituir na fórmula de Bhaskara:

\(x = {-b \pm \sqrt{\Delta} \over 2a}\)

\(x = {-(-4)\ \pm\ \sqrt{4} \over 2\cdot 1}\)

\(x =\frac {4\pm 2} {2 }\)

\(x_1 =\frac {4+2} {2 }= \frac {6} {2}=3\)

\(x_2 =\frac {4-2} {2 }= \frac {2} {2}=1\)

Agora o segundo passo, já que sabemos o valor das raízes. Encontraremos o vértice da parábola:

\(x_v = \frac {-b}{2a} =\frac {-(-4)}{2\ \cdot \ 1} = \frac {4}{2} = 2\)

\(y_v = \frac {-\Delta}{4a} =\frac {-4}{4\ \cdot \ 1} = \frac {-4}{4} = -1\)

\(V(2,-1)\)

O terceiro passo é encontrar o ponto em que a função toca o eixo y. Basta calcular f(0).

f(0) = 0² - 4 ⋅ 0 + 3

f(0) = 3

Importante: Para qualquer função, f(0) = c, ou seja, o ponto em que a função toca o eixo y é igual ao valor do termo independente.

Agora vamos marcar esses 4 pontos encontrados no plano cartesiano, que representaremos por X₁(1,0), X₂(3,0), C(0,3) e V(2,-1), e fazer sua representação gráfica:

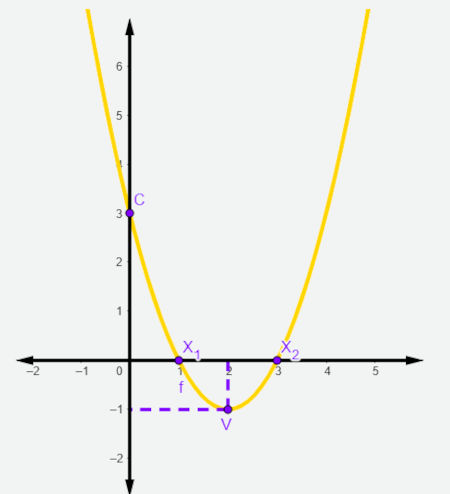
Para saber mais detalhes sobre o gráfico da função do 2º grau, clique aqui.

Exercícios resolvidos sobre função do 2º grau

Questão 1

Um arqueiro atira uma flecha, e a altura f(x) em metros após x segundos é dada pela função quadrática:

f(x) = - 2x² + 8x + 1

Qual é a altura máxima alcançada pela flecha?

A) 9 metros
B) 12 metros
C) 13 metros
D) 15 metros
E) 18 metros

Resolução:

Alternativa A.

Dada a função f(x) = - 2x² + 8x + 1, a altura máxima será o valor de y do vértice da função:

Calculando y_v, temos que:

a = - 2, b = 8 e c =1

\(\Delta = b^2 - 4ac\)

\(\Delta = 8^2 - 4\cdot (-2)\cdot 1\)

\(\Delta = 64 + 8 \)

\(\Delta = 72 \)

Agora, temos que:

\(y_v = \frac {-\Delta}{4a} =\frac {-72}{4\ \cdot \ (-2)} = \frac {-72}{-8} = 9\)

Questão 2

(Enem) Para evitar uma epidemia, a Secretaria de Saúde de uma cidade dedetizou todos os bairros, de modo a evitar a proliferação do mosquito da dengue. Sabe-se que o número f de infectados é dado pela função f(t) = - 2t²+ 120t (em que t é expresso em dia e t = 0 é o dia anterior à primeira infecção) e que tal expressão é válida para os 60 primeiros dias da epidemia.

A Secretaria de Saúde decidiu que uma segunda dedetização deveria ser feita no dia em que o número de infectados chegasse à marca de 1600 pessoas, e uma segunda dedetização precisou acontecer.

A segunda dedetização começou no:

A) 19º dia.

B) 20º dia.

C) 29º dia.

D) 30º dia.

E) 60º dia.

Resolução:

Alternativa B.

Queremos o valor de t para que – 2t² + 120t = 1600.

Logo, temos que:

- 2t² + 120t - 1600 = 0

a = – 2; b = 120 e c = – 1600

\(\Delta = (-120)^2 - 4\cdot 2\cdot 160\)

\(\Delta = 14400 – 12800\)

\(\Delta = 1600\)

Conhecendo o valor de Δ, temos que:

\(t = {-b \pm \sqrt{\Delta} \over 2a}\)

\(t = {-120 \pm \sqrt{1600} \over 2\cdot (-2)}\)

\(t =\frac {-120 \pm 40} { -4}\)

\(t_1 =\frac {-120+ 40} { -4} =\frac {-80} { -4} = 20\)

\(t_2 =\frac {-120- 40} { -4} =\frac {-160} { -4} = 40\)

Sabemos que t₂ tem valor maior que t₁, logo a segunda dedetização será no 20º dia.

Fontes

Dante, L. R. (2017). Matemática: Contexto e Aplicações. 1ª edição. Editora Ática.

Giovanni Jr., J. R., Ruy, J., & Bonjorno, J. R. (2019). Matemática: Contexto e Aplicações. 2ª edição. Editora FTD.

Iezzi, G., de Souza, C. M. F., de Oliveira, H., & de Oliveira, V. (2019). Fundamentos de Matemática Elementar. 11ª edição. Editora Atual.