Uma função é uma regra que relaciona cada elemento de um conjunto a um único elemento de um outro conjunto. Esses dois conjuntos são chamados de domínio e contradomínio, respectivamente. Dadas duas funções distintas f e g, se o domínio da função g for o contradomínio da função f, é possível construir uma função composta gof, cujo domínio é igual ao domínio da função f e o contradomínio é igual ao contradomínio da função g.
Definição de função composta
Dadas as funções f: A → B e g: B → C, a função composta de g com f é a função h(x) = g(f(x)), que também pode ser escrita como gof(x). Essa última notação pode ser lida “g bola f”.
Em outras palavras, escolhido um elemento x do domínio, aplica-se sobre ele a função f e, depois, sobre o resultado. A função g tem o mesmo resultado que aplicar a função composta:
h: A → C
Domínio e contradomínio em diagramas
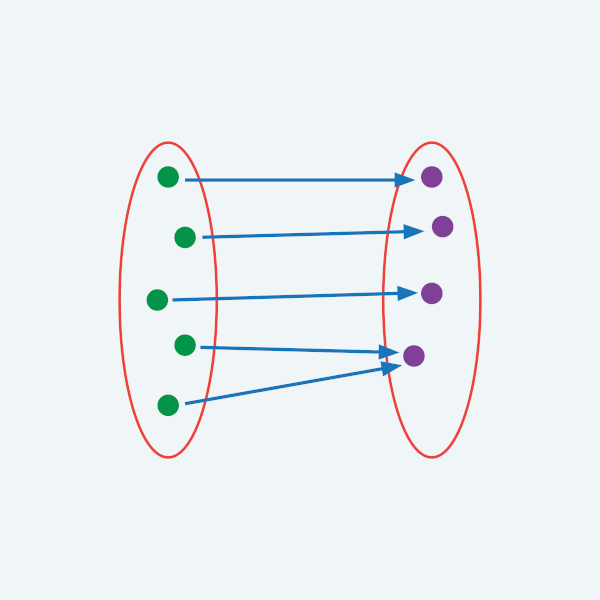
Para compreender melhor a estrutura de uma função composta, observe o diagrama a seguir:
O conjunto A é o domínio da função f; o conjunto B é o contradomínio da função f e o domínio da função g; e o conjunto C é o contradomínio da função g.
Observe que existem dois caminhos para a composição das funções f e g. O primeiro é aplicar a função f a um elemento de seu domínio, e depois aplicar a função g ao resultado obtido. O segundo é aplicar a função h a um elemento do conjunto A e já obter um resultado do conjunto C diretamente.
Composição de funções na prática
Compor as funções f e g, obtendo gof, é substituir a variável da função g por toda a função f. Os exemplos a seguir mostram como fazer a composição entre duas funções.
Dadas as funções:
f: R → R
f(x) = 2x + 3
e
g: R → R
g(x) = x2
Observe que o contradomínio da função f é igual ao domínio da função g. Assim, é fácil compor as duas funções, fazendo:
gof(x) = g(f(x)) = (2x + 3)2
Na prática, apenas substituímos a variável x da função g por toda a função f. Agora note o resultado de gof(3):
f(3) = 2·3+3 = 9
g(9) = 92 = 81
Usando a composta, teremos:
gof(3) = (2·3 + 3)2 = (6 + 3)2 = (9)2 = 81
Aproveite para conferir nossa videoaula sobre o assunto: