A função afim é a função com domínio e contradomínio no conjunto dos números reais, com lei de formação do tipo \(f(x)=ax+b\). A função afim é conhecida também como função polinomial do 1º grau.
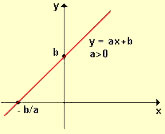
O gráfico da função afim é sempre representado por uma reta, que pode ser crescente ou decrescente. Na lei de formação da função, a e b são os coeficientes da função, a é o coeficiente angular e b é o coeficiente linear. Se o coeficiente angular a for positivo, a reta é crescente; se a é negativo, a reta é decrescente. O coeficiente linear b nos informa o valor de y em que a reta corta o eixo y.
Leia também: Função linear — uma função afim que possui b = 0
Tópicos deste artigo
- 1 - Resumo sobre função afim
- 2 - Fórmula da função afim
- 3 - Como se calcula a função afim?
- 4 - Zero da função afim
- 5 - Gráfico da função afim
- 6 - Coeficiente angular e coeficiente linear de uma função afim
- 7 - Tipo de função afim
- 8 - Exercícios resolvidos sobre função afim
Resumo sobre função afim
-
A função afim é a função com domínio e contradomínio no conjunto dos números reais.
-
Sua fórmula ou lei de formação é \(f(x)=ax+b\).
-
Na lei de formação, a é o coeficiente angular e b é o coeficiente linear.
-
O zero de uma função afim é o valor x que faz com que f(x) seja igual a 0.
-
O gráfico da função afim é sempre uma reta.
-
A reta pode ser crescente ou decrescente.
-
Se na lei de formação a for positivo, o gráfico da função é crescente.
-
Se na lei de formação a for negativo, o gráfico da função é decrescente.
-
-
Na função afim, o coeficiente angular é o número real que acompanha a variável x e o coeficiente linear é o termo independente da função.
-
A função afim pode ser crescente, constante e decrescente.
Fórmula da função afim
A função afim é uma função com domínio e contradomínio no conjunto dos números reais. Sua fórmula, conhecida como lei de formação, é descrita por:
\(f(x)=ax+b\)
-
a → coeficiente angular.
-
b → coeficiente linear.
-
x → variável independente.
-
f(x) → variável dependente.
Exemplos:
-
f(x) = 2x – 4
-
f(x) = – 3x + 1
-
f(x) = 2x
-
f(x) = – x – 3
Como se calcula a função afim?
Conhecendo a lei de formação da função afim, podemos calcular o valor numérico da função. Para isso, basta substituir o valor de x na função e encontrar a imagem da função para aquele determinado valor.
Exemplo:
Dada a função f(x) = 2x – 4, calcule o valor numérico da função para:
A) x = 3
B) x = - 1
Resolução:
A) Substituindo x por 3, temos que:
\(f(3)=2⋅3-4\)
\(f(3)=6-4\)
\(f(3)=2\)
Então, a imagem da função para x = 3 é 2.
B) Substituindo x por - 1, temos que:
\(f(-1)=2⋅(-1)-4\)
\(f(-1)=-2-4\)
\(f(-1)=- 6\)
Então, a imagem da função para x = - 1 é - 6.
Zero da função afim
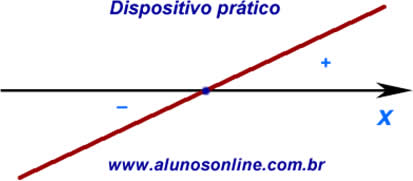
O zero de uma função afim é o valor x que faz com que f(x) seja igual a 0. Para encontrar o valor do zero da função, basta igualar a função a zero. De modo geral, para calcular o zero da função, temos que:
\(ax+b=0\)
\(ax=-b\)
Assim, o zero da função é:
\(x=\frac{-b}a\)
Exemplo:
Encontre o zero da função f(x) = 3x – 12.
Resolução:
Calculando o zero da função, temos que:
\(3x-12=0\)
\(3x=12 \)
\(x=\frac{12}3\)
\(x=4\)
Prova real:
Se substituirmos x = 4 na função, encontraremos f(x) = 0.
\(f(4)=3⋅4-12\)
\(f(4)=12-12\)
\(f(4)=0\)
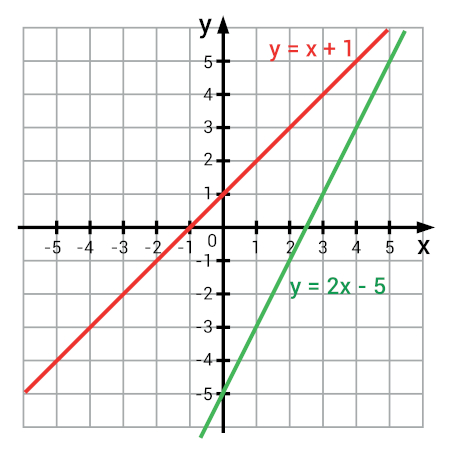
Gráfico da função afim
O gráfico de uma função afim é sempre uma reta, podendo ser crescente ou decrescente. Para fazer a representação de uma função afim no gráfico, encontramos pares ordenados (x, y) que satisfazem a lei de formação da função.
Exemplo:
Construa o gráfico da função \(f(x)=2x-1\).
Resolução:
Para fazer a representação gráfica dessa função, atribuiremos alguns valores para x e encontraremos a sua imagem y:
\(f(-2)=2⋅(-2)-1=- 4-1=- 5\)
\(f(-1)=2⋅(-1)-1=- 2-1=- 3\)
\(f(0)=2⋅0-1=0-1=- 1\)
\(f(1)=2⋅1-1=2-1=1\)
\(f(2)=2⋅2-1=4-1=3\)
Então, sabemos que os pontos A(-2, -5), B( -1, -3), C(0, - 1), D(1, 1) e E(2, 3) são pontos que pertencem ao gráfico da função. Agora, basta fazer a representação desses pontos no plano cartesiano e traçar a reta que passa por eles:
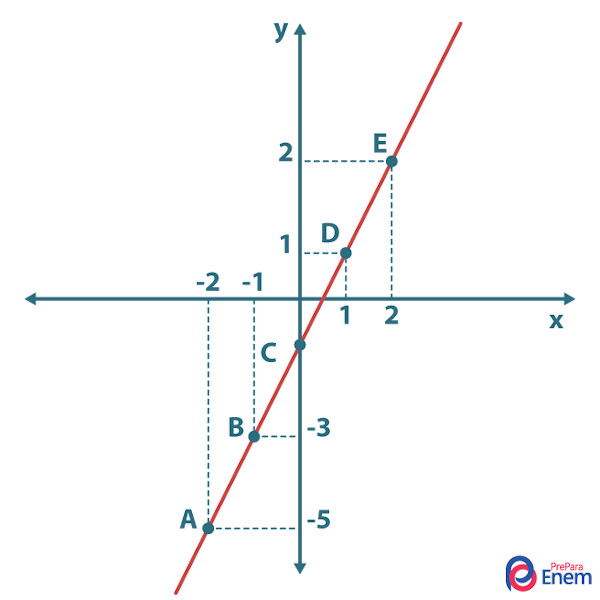
Para construir o gráfico de uma função afim, são necessários somente dois pontos. No caso, utilizamos 5, mas 2 pontos é o suficiente para fazer a representação gráfica da função.
Coeficiente angular e coeficiente linear de uma função afim
Conhecemos como coeficiente angular da função afim o número real que acompanha a variável x e como coeficiente linear da função o termo independente da função. Logo, na lei de formação, temos que:
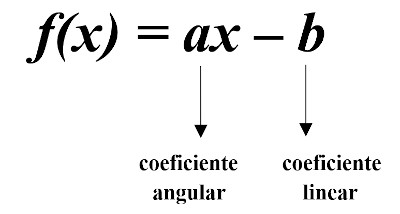
Exemplo:
Na função f(x) = 3x – 4, o coeficiente angular a = 3 e o coeficiente linear b = - 4.
→ Coeficiente angular
Como o nome sugere, o coeficiente angular permite descobrir informações sobre o ângulo que a reta faz com o eixo horizontal. O coeficiente angular nos permite saber se a função é crescente, decrescente ou constante. Podemos dividir em 3 casos:
-
Se a > 0, ou seja, se o coeficiente angular for positivo, a função é crescente.
-
Se a = 0, a função é constante.
-
Se a < 0, ou seja, se o coeficiente angular for negativo, a função é decrescente.
→ Coeficiente linear
O coeficiente linear é o ponto em que a reta corta o eixo y, que é o ponto (0, b).
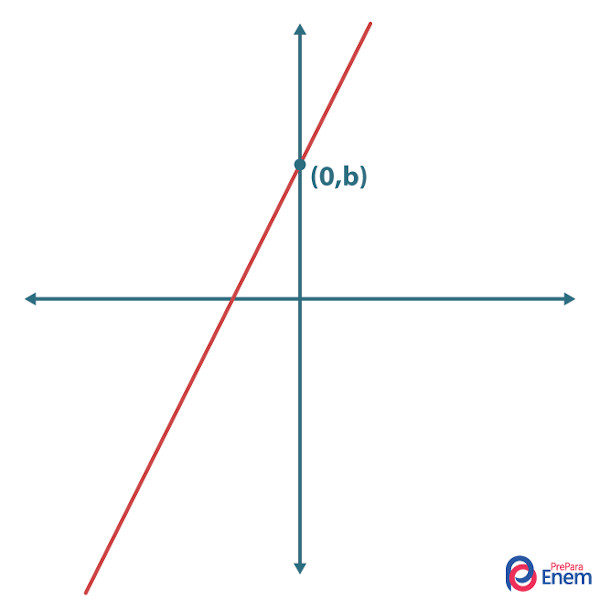
Tipo de função afim
A função afim pode ser dividida em três casos: função afim crescente, função afim constante e função afim decrescente. Veremos cada tipo a seguir.
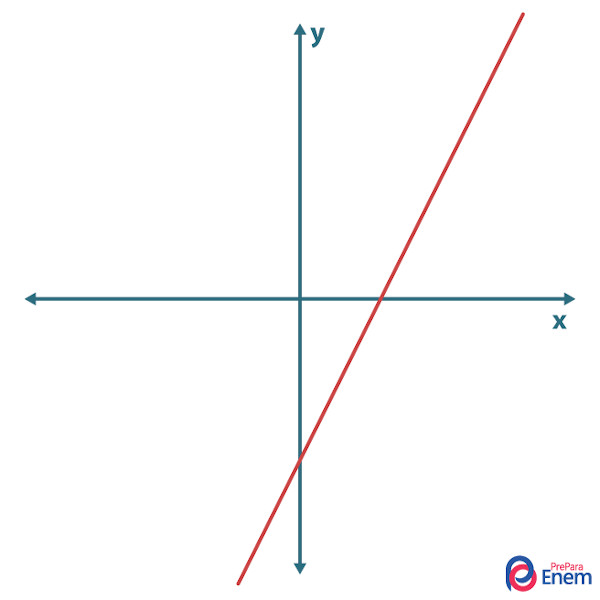
→ Função afim crescente
A função afim é crescente se o coeficiente angular for positivo. O comportamento crescente quer dizer que à medida que o valor de x aumenta na função, o valor de f(x) também aumenta.
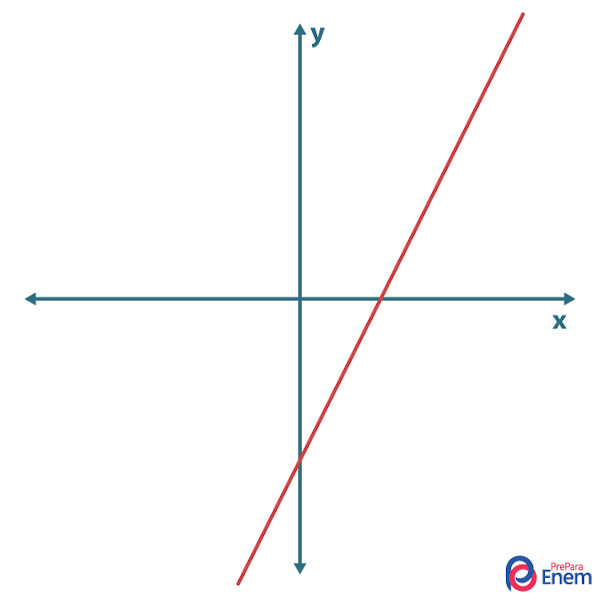
→ Função afim constante
A função afim é constante quando o coeficiente angular é 0. A função é constante quando o valor de y é sempre o mesmo para todos os valores de x.
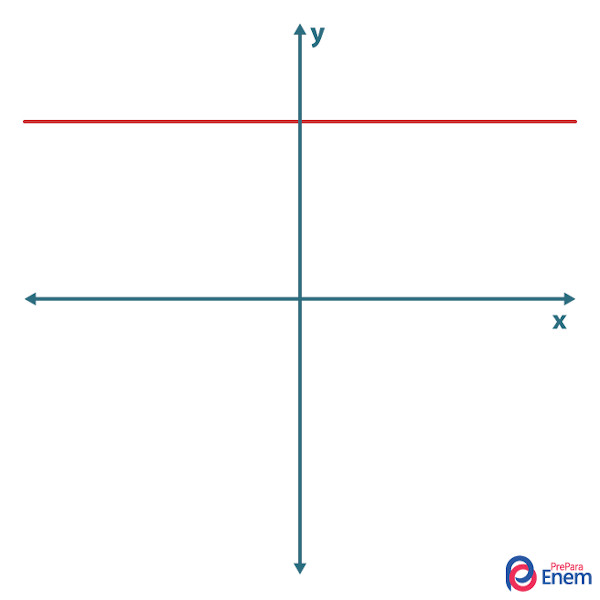
→ Função afim decrescente
A função afim é decrescente quando o seu coeficiente angular é negativo. Ser decrescente significa que à medida que o valor de x aumenta, o valor de y diminui na função.
Veja também: Função sobrejetora — a função em que o conjunto do contradomínio é igual ao conjunto imagem da função
Exercícios resolvidos sobre função afim
Questão 1
Qual é o valor do zero da função \(f(x)=2x+6\)?
A) 2
B) – 2
C) 3
D) – 3
E) 6
Resolução:
Alternativa D
Calculando o zero da função, temos que:
\(2x+6=0\)
\(2x=- 6\)
\(x=\frac{-6}2\)
\(x=-3\)
Questão 2
O valor a ser cobrado por um serviço de limpeza é dado pela função afim \(f(t)=25t+45\), em que t é o tempo gasto para executar esse serviço em horas. Se um cliente contratar esse serviço por 4 horas, então o valor pago por ele será de:
A) R$ 65,00
B) R$ 100,00
C) R$ 145,00
D) R$ 260,00
Resolução:
Alternativa C
Queremos calcular o valor de f(4), portanto:
\(f(4)=25⋅4+45\)
\(f(4)=100+45\)
\(f(4)=145\)
O valor pago por esse cliente será de R$ 145,00.