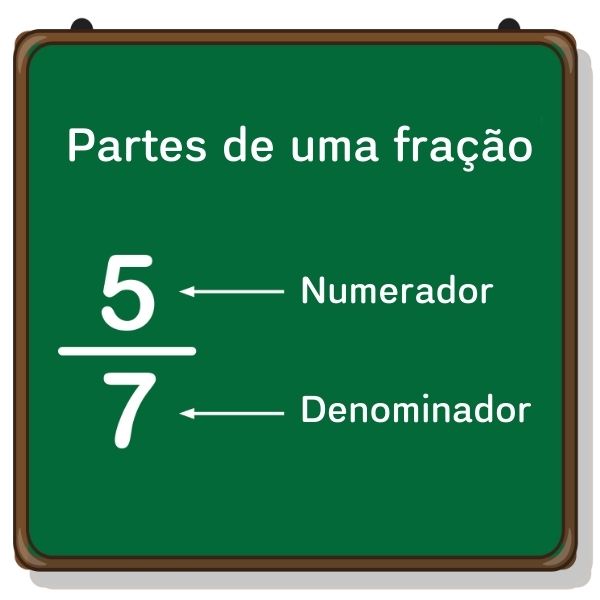
A fração é uma representação de uma divisão. Na parte de cima dela, escrevemos quantas partes temos, e na parte de baixo, escrevemos em quantas partes o todo foi dividido. O número de cima de uma fração é conhecido como numerador, e o que está embaixo é o denominador.
É possível realizar várias operações envolvendo a fração, como adição, multiplicação, subtração e divisão. Vale destacar que, de acordo com as características que as frações possuem, elas podem ser classificadas em:
-
própria;
-
imprópria;
-
aparente;
-
mista;
-
equivalentes;
-
irredutível.
Leia também: Como fazer divisão com números decimais?
Tópicos deste artigo
- 1 - O que é fração?
- 2 - Tipos de fração
- 3 - Operações com frações
- 4 - Exercícios resolvidos sobre frações
O que é fração?
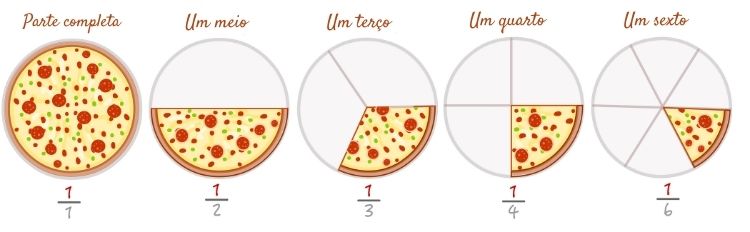
Conhecemos como fração a maneira de representar uma quantidade por meio de uma razão, ou seja, uma divisão, entre dois números. Em uma fração, o número de cima é conhecido como numerador e o número de baixo como denominador.

-
Exemplos de fração
\(\frac{\mathbf{1}}{\mathbf{5}}\)
(Lê-se 1 sobre 5.)
\(\frac{\mathbf{12}}{\mathbf{35}}\)
(Lê-se 12 sobre 35.)
\(\frac{\mathbf{29}}{\mathbf{6}}\)
(Lê-se 29 sobre 6.)
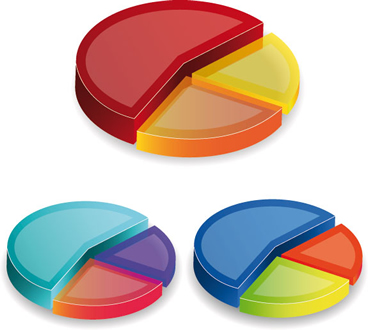
Uma interpretação interessante para frações é a geométrica, em que o numerador representa a quantidade de partes a se considerar e o denominador representa o número de partes em que o todo foi divido:
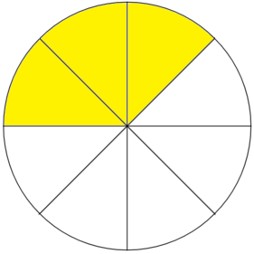
Podemos representar a relação entre a parte amarela e o número de partes que o círculo foi dividido, que, no caso, é a fração:
\(\frac{\mathbf{3}}{\mathbf{8}}\)
→ Videoaula sobre fração
Tipos de fração
-
Fração própria
Quando o numerador é menor que o denominador. Exemplos:
\(\frac{1}{2\ }\ \ \ \ \ \frac{5}{11}\ \ \ \ \frac{9}{10}\)
-
Fração imprópria
Quando o numerador é maior que o denominador. Exemplos:
\(\frac{8}{5}\ \ \ \ \frac{11}{2}\ \ \ \ \frac{20}{18}\)
-
Fração aparente
Quando a divisão entre o numerador e o denominador for um número inteiro. Exemplos:
\(\frac{8}{8}\ \ \ \ \frac{12}{4}\ \ \ \ \frac{15}{3}\)
Todas as três frações são aparentes, pois sabemos que:
8 : 8 = 1
12 : 4 = 3
15 : 3 = 5
Quando dividimos o numerador pelo denominador, nos três casos, encontramos um número inteiro como resposta.
-
Frações equivalentes
Quando representam a mesma parte em relação ao todo, ou seja, representam a mesma quantidade.
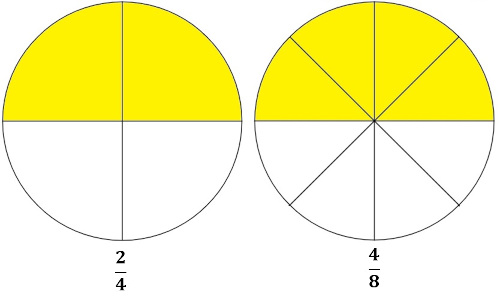
Note que as frações \(\frac{\mathbf{2}}{\mathbf{4}}\) e \(\frac{\mathbf{4}}{\mathbf{8}}\) representam a mesma parte de um objeto, logo, dizemos que elas são equivalentes. É possível perceber que, ao multiplicar o numerador e o denominador da fração \(\frac{2}{4}\) por 2, encontraremos a fração \(\frac{4}{8}\).
Dada uma fração, existem infinitas frações equivalentes a ela, e para encontrá-las, basta multiplicar o numerador e o denominador pelo mesmo número.
-
Frações irredutíveis
Quando não há nenhum número que divide o numerador e o denominador ao mesmo tempo.
Dada uma fração, quando é possível dividir o numerador e o denominador por um mesmo número, o resultado é uma fração equivalente, logo, para escrevê-la na forma mais simples possível, dividimos o numerador e o denominador por um mesmo número, até que não exista nenhum número que os divida ao mesmo tempo. Quando isso acontece, encontramos uma fração irredutível.
Exemplo:
\(\frac{16}{12}\)
Encontraremos o menor número que divide 16 e 12 ao mesmo tempo, que, no caso, é o 4. Assim faremos uma simplificação dessa fração dividindo por 4 tanto o numerador quanto o denominador.
\(\frac{{16}^{:4}}{{12}_{:4}}=\frac{4}{3}\)
Então a fração \(\frac{4}{3}\) é a forma simplificada da fração anterior. Note que não há nenhum outro número diferente de 1 que divide tanto o 4 quanto o 3 ao mesmo tempo, então essa fração é irredutível. Outros exemplos desse tipo:
\(\frac{2}{5}\ \ \ \frac{11}{15}\ \ \ \frac{25}{23}\)
-
Fração mista
É feita por um número inteiro seguido de uma fração, então escrevemos a parte inteira e a parte fracionária da quantidade.
Exemplo:
\(2\frac{3}{5}\)
Essa fração representa 2 inteiros e \(\frac{3}{5}\).
Outros exemplos:
\(3\frac{1}{2}\ \ \ \ \ \ 5\frac{2}{7}\)
Confira na nossa videoaula: Tipos de frações
Operações com frações
Veja como realizar a adição, a subtração, a multiplicação e a divisão entre frações.
-
Adição e subtração de frações
Podemos separar a adição e a subtração de frações em dois casos. O primeiro deles é quando os denominadores são iguais, e o segundo é quando eles são diferentes.
-
-
1º caso: denominadores iguais
-
Basta realizar a adição/subtração com os numeradores da fração e conservar o denominador.
Exemplos:
\(\frac{1}{7}+\frac{5}{7}=\frac{5+1}{7}=\frac{6}{7}\)
\(\frac{4}{9}-\frac{3}{9}=\frac{4-3}{9}=\frac{1}{9}\)
-
-
2º caso: quando os denominadores são diferentes
-
É necessário encontrar frações equivalentes, de forma que o denominador delas se iguale, para isso, deve-se encontrar o mínimo múltiplo comum (MMC) dos denominadores, como no exemplo a seguir.
Exemplo 1:
\(\frac{2}{5}+\frac{3}{8}\)
Note que o denominador é diferente, então é necessário encontrar o MMC entre 5 e 8.
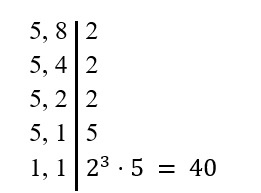
Sabendo que o MMC é igual a 40, então multiplicaremos o numerador e o denominador das duas frações de modo que o resultado seja igual a 40.
Na primeira fração, sabemos que 40 : 5 = 8, então é necessário multiplicar o numerador e o denominador por 8:
\(\frac{2\cdot8}{5\cdot8}=\frac{16}{40}\)
Na segunda fração, sabemos que 40 : 8 = 5, então multiplicaremos o numerador e o denominador por 5:
\(\frac{3\cdot5}{8\cdot5}=\frac{15}{40}\)
Agora que encontramos as frações equivalentes, com os mesmos denominadores, podemos realizar a soma dos numeradores.
\(\frac{16}{40}+\frac{15}{40}=\frac{16+15}{40}=\frac{31}{40}\)
Exemplo 2:
\(\frac{11}{20}-\frac{5}{12}\)
Como os denominadores são diferentes, calcularemos o MMC:
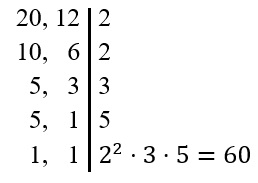
Como o MMC é 60, na primeira fração temos que 60 : 20 = 3, logo, multiplicaremos por 3 o numerador e o denominador da primeira fração:
\(\frac{11\cdot3}{20\cdot3}=\frac{33}{60}\)
Na segunda fração, temos que 60 : 12 = 5, então multiplicaremos o denominador e o numerador por 5:
\(\frac{5\cdot5}{12\cdot5}=\frac{25}{60}\)
Agora que reescrevemos as frações com os mesmos denominadores, é possível realizar a subtração.
\(\frac{33}{60}-\frac{25}{60}=\frac{8}{60}\)
Perceba que essa fração pode ser simplificada dividindo por 4 o numerador e o denominador da resposta. Assim ela ficará irredutível:
\(\frac{8^{:4}}{{60}_{:4}}=\frac{2}{15}\)
-
Multiplicação de frações
Para multiplicar duas frações, calculamos o produto entre os numeradores e o produto entre os denominadores, encontrando uma nova fração.
Exemplo:
\(\frac{5}{12}\cdot\frac{3}{4}=\frac{5\cdot3}{12\cdot4}=\frac{15}{48}\)
Perceba que, nesse caso, é possível simplificar a fração encontrada:
\(\frac{{15}^{:3}}{{48}_{:3}}=\frac{5}{16}\)
-
Divisão de frações
Para calcular a divisão entre duas frações, multiplicamos cruzado, ou seja, o numerador da primeira fração pelo denominador da segunda, e o denominador da primeira pelo segundo numerador.
Exemplo:
Calcularemos a divisão \(\frac{3}{5}:\frac{2}{7}\):
\(\frac{\mathbf{3}}{5}:\frac{2}{\mathbf{7}}=\frac{\mathbf{3}\cdot\mathbf{7}}{5\cdot2}=\frac{\mathbf{21}}{10}\)
Leia também: Operações matemáticas básicas
Exercícios resolvidos sobre frações
Questão 1
Julgue as afirmativas a seguir:
I. As frações \(\frac{2}{9}\) e \(\frac{26}{117}\) são equivalentes.
II. A fração \(\frac{81}{9}\) é aparente.
Sobre as afirmativas I e II, marque a alternativa correta:
A) somente a I é verdadeira.
B) somente a II é verdadeira.
C) nenhuma das afirmativas é verdadeira.
D) todas as afirmativas são verdadeiras.
Resolução:
Alternativa D
I. As frações \(\frac{2}{9} \) e \(\frac{26}{117}\) são equivalentes. (verdadeira)
Se simplificarmos a segunda fração, dividindo por 13, encontraremos a primeira:
\(\frac{{26}^{:13}}{{117}_{:13}}=\frac{2}{9}\)
II. A fração \(\frac{81}{27}\) é aparente. (verdadeira)
Ao dividir 81 por 27, temos 81: 27 = 3. Como a resposta é um número inteiro, então a fração é aparente.
A resposta, portanto, é a letra D.
Questão 2
(FGV) Certa quantia foi repartida entre os irmãos Alceu, Breno e Caio. Alceu recebeu a terça parte do total, e Breno recebeu dois quintos do total. A fração do total que coube a Caio é
A) 3/8.
B) 5/8.
C) 11/15.
D) 9/15.
E) 4/15.
Resolução:
Alternativa E
Sabemos que havia uma quantia inteira 1, e que dela foram tirados um terço \(\left(\frac{1}{3}\right)\) e dois quintos \(\left(\frac{2}{5}\right)\) , logo, a quantia que coube a Caio pode ser calculada por:
\(1-\frac{1}{3}-\frac{2}{5}\)
O mínimo múltiplo comum entre 3 e 5 é 15, logo, temos que:
\(\frac{15}{15}-\frac{5}{15}-\frac{6}{15}\)
\(\frac{15-5-6}{15}\)
\(\frac{4}{15}\)