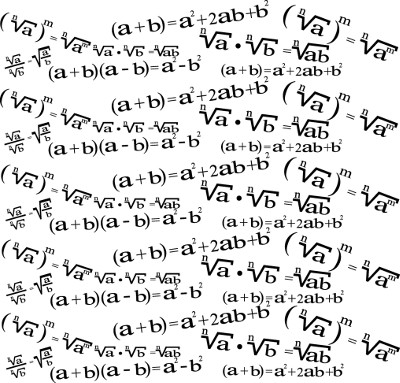Frações algébricas são expressões munidas de pelo menos uma incógnita no denominador. Tendo em vista que incógnitas representam números reais ainda desconhecidos, é possível afirmar que as frações algébricas também representam números reais. Dessa forma, todas as operações válidas para esse conjunto numérico também são válidas para as frações algébricas, a saber: adição, subtração, multiplicação e divisão.
Quando essas operações envolvem frações algébricas, pode ser necessário apelar para outras propriedades matemáticas, como propriedades de potências, fatoração de polinômios, produtos notáveis etc.
Veja um exemplo de fração algébrica:
4x3y2
3k2a
Simplificação de fração algébrica
A simplificação de frações algébricas faz uso de propriedades de potências e, algumas vezes, de fatoração de polinômios. A tentativa é de escrever a fração algébrica na forma mais fatorada possível e eliminar o excesso de incógnitas repetidas no numerador e denominador por meio da divisão de potências de mesma base. Observe o exemplo:
4a3(a2 + 2ab + b2)
16a2(a2 – b2)
Observe que os elementos presentes no numerador podem ser fatorados por dois procedimentos diferentes: o número 4 se transformará em 22 e o polinômio a2 + 2ab + b2, que é um trinômio quadrado perfeito, poderá ser reescrito na forma (a + b)2.
Já o denominador também pode ser fatorado ao rescrever 16 como 24 e a2 – b2, que é uma diferença de dois quadrados, como (a + b)(a – b). Substituindo essas formas fatoradas na fração algébrica dada, obteremos:
22a3(a + b)2
24a2(a + b)(a – b)
Agora, elimine aquilo que aparece repetido no numerador e no denominador. Para facilitar esse processo, as potências podem ser expandidas. Observe:
2·2·a·a·a·(a + b)·(a + b)
2·2·2·2·a·a·(a + b)(a – b)
Em azul, estão os fatores que se repetem e que serão eliminados. O resultado será o seguinte:
a(a + b)
2·2(a – b)
Essa é a forma simplificada da fração algébrica dada como exemplo.
Adição e subtração de fração algébrica
As duas operações são feitas da mesma maneira. Se os denominadores das frações algébricas forem iguais, basta somar/subtrair os numeradores e repetir os denominadores no resultado. Por exemplo:
4xy + 2xy = 4xy + 2xy = 6xy
k k k k
Se os denominadores forem diferentes, teremos que: encontrar frações equivalentes àquelas que queremos somar/subtrair e depois somar/subtrair as frações equivalentes. O procedimento para isso pode ser resumido em alguns passos:
-
Calcular o mínimo múltiplo comum dos denominadores. Como os denominadores são polinômios, o procedimento para encontrar esse MMC pode ser obtido aqui. Antes de calcular o MMC dos denominadores, pode ser necessário fatorá-los. Os processos de fatoração mais importantes podem ser encontrados aqui;
-
Encontrar frações equivalentes àquelas que devem ser somadas/subtraídas;
-
Para isso, o processo é o mesmo usado nas frações numéricas: dividimos o MMC pelo denominador de cada fração e multiplicamos o resultado pelo respectivo numerador. Os valores obtidos serão os numeradores das frações equivalentes;
-
Somar/subtrair os numeradores exatamente como é feito para frações com denominadores iguais.
Para exemplos e mais detalhes a respeito da soma de frações numéricas, clique aqui. Para obter exemplos e mais detalhes sobre adição de frações algébricas, clique aqui.
Multiplicação de fração algébrica
A multiplicação de frações algébricas é exatamente igual à multiplicação de frações numéricas: multiplica-se numerador por numerador e denominador por denominador. A diferença é que, após a multiplicação, é importante analisar se o resultado obtido pode ser simplificado. Esse processo de simplificação é semelhante ao que discutimos no início do texto. Por exemplo:
5xy ·11xk = 5xy ·11xk = 55x2yk = 55
kx yx kx·yx kx2y
Divisão de fração algébrica
Também é feita de modo idêntico à divisão entre frações numéricas. Para tanto, multiplique a primeira fração pelo inverso da segunda. Para encontrar o inverso de uma fração, basta trocar numerador e denominador de lugar. Observe a divisão de frações no exemplo a seguir:
44x2yz : 11xyz = 44x2yz · kh
kh2 kh kh2 11xyz
Após isso, basta realizar a multiplicação e simplificar o resultado:
44x2yz · kh = 44x2yzkh = 4x
kh2 11xyz 11xyzkh2 h