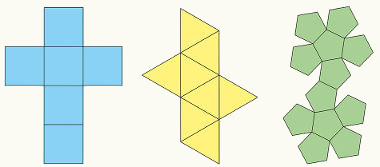
Formas geométricas são os formatos dos objetos ao nosso redor. A Geometria (“ciência de medir terras”, do grego geometrein) é o ramo da Matemática que estuda as formas geométricas. Essa área do conhecimento analisa as medidas, o tamanho e a posição das formas no ambiente bidimensional e tridimensional.
Leia também: Congruência de figuras geométricas — os casos em que figuras distintas possuem medidas iguais
Tópicos deste artigo
- 1 - Resumo sobre formas geométricas
- 2 - Quais são as formas geométricas?
- 3 - Fractais
- 4 - Exercícios resolvidos sobre formas geométricas
Resumo sobre formas geométricas
-
As formas geométricas são os objetos estudados pela Geometria.
-
Classificamos as formas geométricas em formas planas e formas não planas.
-
As formas geométricas planas possuem largura e comprimento, mas não espessura, sendo bidimensionais. Essas formas são divididas em polígonos e não polígonos.
-
Triângulos, quadrados, retângulos e pentágonos são exemplos de formas geométricas planas.
-
As formas geométricas não planas (espaciais) possuem largura, comprimento e espessura, sendo tridimensionais. Essas formas são divididas em poliedros e não poliedros (corpos redondos).
-
Prismas e pirâmides são exemplos de formas geométricas espaciais, ou seja, de sólidos geométricos.
-
Fractais são formas geométricas intricadas, com padrões contínuos.
Quais são as formas geométricas?
As formas geométricas podem ser classificadas em planas ou não planas, dependendo se possuem duas ou três dimensões, respectivamente. Vejamos algumas das formas geométricas mais importantes.
→ Formas geométricas planas

Formas geométricas planas estão restritas ao plano, ou seja, ao ambiente bidimensional. Essas formas possuem largura e comprimento, porém não possuem espessura. São estudadas na Geometria Plana. Podemos subdividir as formas planas em polígonos ou não polígonos.
◦ Polígonos
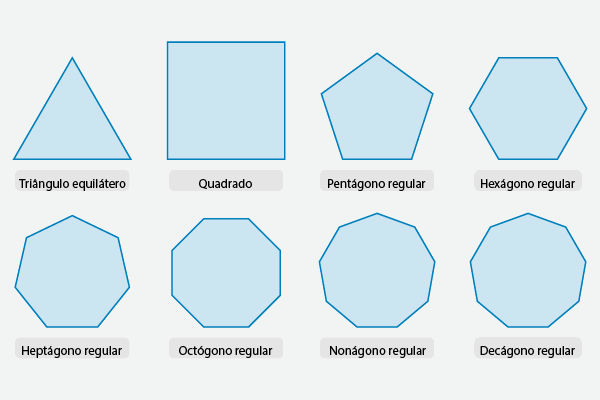
Os polígonos são figuras geométricas planas e fechadas delimitadas por segmentos de reta que se tocam somente nas extremidades. Os segmentos são chamados de lados, e as extremidades, de vértices do polígono. Exemplos comuns de polígonos são: triângulo, quadrado, retângulo, pentágono e hexágono.
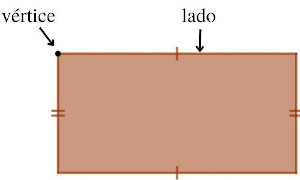
Um polígono é um polígono convexo quando dados dois pontos quaisquer em seu interior, o segmento com extremidades nesses pontos também está no interior do polígono. Quando isso não ocorre, o polígono é um polígono não convexo.
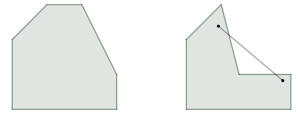
Ainda, um polígono é um polígono regular quando é convexo e possui todos os lados e ângulos congruentes. Se pelo menos um lado não for congruente, o polígono é um polígono irregular.
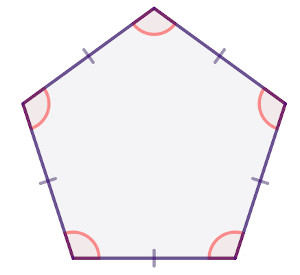
◦ Não polígonos

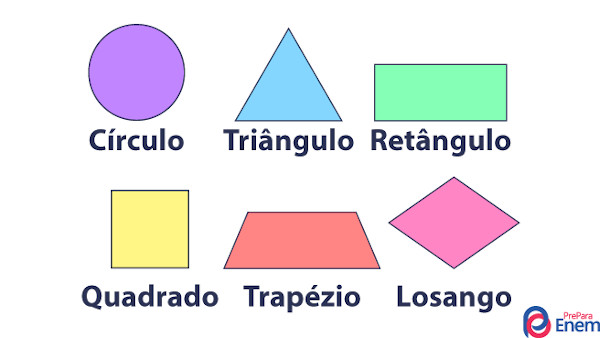
Figuras geométricas planas abertas, curvas ou formadas por segmentos que se cruzam em outros pontos além das extremidades não são consideradas polígonos. Exemplos comuns de não polígonos são: circunferência, círculo e elipse.
Saiba mais: Polígonos semelhantes — a igualdade entre ângulos e a proporcionalidade entre lados correspondentes
→ Formas geométricas não planas
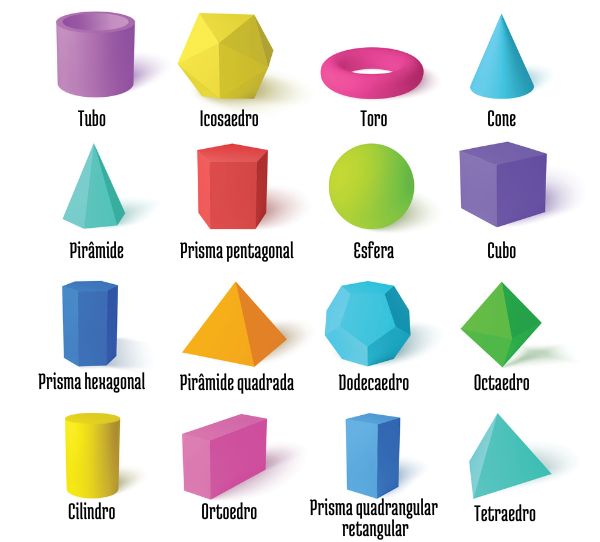
Formas não planas, também chamadas de sólidos geométricos, são objetos tridimensionais. Essas formas possuem comprimento, largura e espessura. São estudadas na Geometria Espacial. Podemos separar os sólidos geométricos em poliedros ou não poliedros.
◦ Poliedros
Os poliedros são formas tridimensionais cujas faces são polígonos. Os segmentos que delimitam as faces são chamados de arestas, e as extremidades dos segmentos são os vértices do poliedro. Exemplos comuns de poliedros são o cubo, o prisma e a pirâmide.
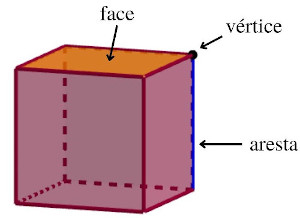
Um poliedro é um poliedro convexo se dados dois pontos quaisquer em seu interior, o segmento com extremidades nesses pontos também está no interior do poliedro. Uma propriedade importante dos poliedros convexos é que eles satisfazem a Relação de Euler (V + F = A + 2). Quando isso não ocorre, o poliedro é um poliedro não convexo.
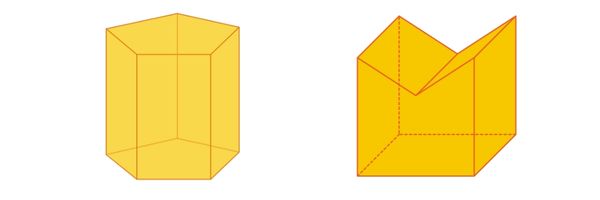
Além disso, um poliedro é um poliedro regular se todas as suas faces são polígonos regulares e congruentes e se os ângulos são congruentes. Existem cinco tipos de poliedros regulares: tetraedro regular, cubo (hexaedro regular), octaedro regular, dodecaedro regular e icosaedro regular. Quando o poliedro não atende a esses critérios, é um poliedro irregular.
◦ Não poliedros
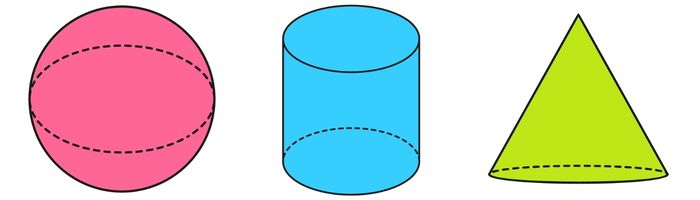
Também conhecidos como corpos redondos, os sólidos geométricos cujas faces não são polígonos não são poliedros. Exemplos comuns de não poliedros são: esfera, cilindro e cone.
◦ Sólidos de Platão
Os sólidos de Platão são poliedros que satisfazem três condições:
-
são poliedros convexos;
-
todas as faces têm o mesmo número de arestas;
-
todos os vértices são extremidades do mesmo número de arestas.
Consequentemente, existem cinco classes de sólidos de Platão: tetraedro, hexaedro (cubo), octaedro, dodecaedro e icosaedro.
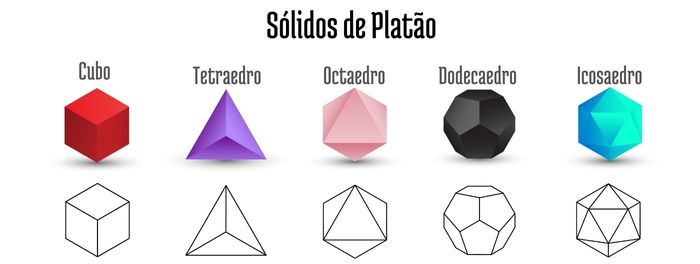
Importante: perceba que todo poliedro regular é sólido de Platão, mas nem todo sólido de Platão é poliedro regular.
Saiba também: Como é feita a planificação de sólidos geométricos?
Fractais
Fractais são formas geométricas complexas, ligadas à percepção do infinito. O termo fractal tem origem no latim: adjetivo fractus e verbo fragere, que significa quebrar, fragmentar. Assim, um fractal é um objeto geométrico que possui uma estrutura repetitiva, independente da distância de observação.

Diferentes padrões fractais podem ser encontrados na natureza, como em flocos de neve, folhas de samambaia e galhos de árvores. O ramo da Matemática que estuda essas formas se chama Geometria Fractal e está associada ao estudo do Caos.
Exercícios resolvidos sobre formas geométricas
Questão 1
(Enem) No desenho técnico, é comum representar um sólido por meio de três vistas (frontal, perfil e superior), resultado da projeção do sólido em três planos, perpendiculares dois a dois. A figura representa as vistas de uma torre.
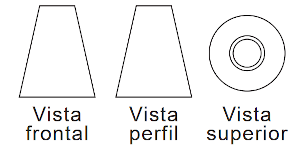
Com base nas vistas fornecidas, qual figura melhor representa essa torre?
A) 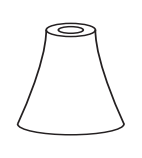
B) 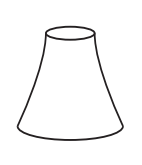
C) 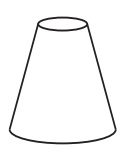
D) 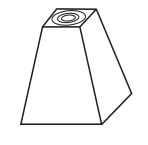
E) 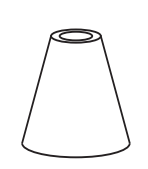
Resolução:
Alternativa E
Por meio das vistas apresentadas, o sólido procurado deve possuir:
-
uma base superior em formato de anel e uma base inferior circular;
-
superfícies laterais cujas secções meridianas formem quadriláteros.
Assim, somente o último sólido representa a torre.
Questão 2
(Enem) A figura seguinte mostra um modelo de sombrinha muito usado em países orientais.
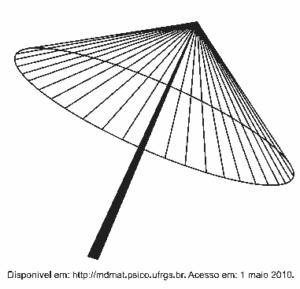
Esta figura é uma representação de uma superfície de revolução chamada de
A) pirâmide.
B) semiesfera.
C) cilindro.
D) tronco de cone.
E) cone.
Resolução:
Alternativa E
Observe que a parte superior da sombrinha é uma superfície de revolução, um cone com base circular e vértice superior.