No estudo do sinal da função afim, buscamos os intervalos nos quais a função possui certas características. Lembrando que os valores das funções dependem unicamente da sua variável e da sua lei de formação.
A forma geral de uma função do 1º grau dá-se da seguinte maneira:

Teremos duas situações a serem analisadas, quanto ao sinal dessa função.
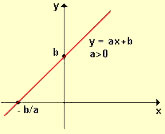
a > 0: Função crescente.

Temos que o valor para x=r consiste na raiz da função, ou seja, no zero da função. Partindo desse zero podemos analisar os dois possíveis sinais de uma função (positivo e negativo).
Note no gráfico que:

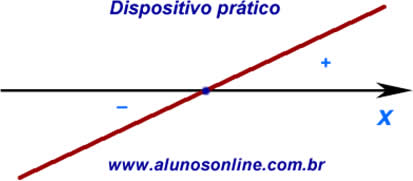
Caso você não queira construir todo o gráfico, basta encontrar o zero da função e analisar o sinal da função na reta dos reais da variável x. Para isso, use o dispositivo prático, mostrado a seguir:

Note que os sinais (positivo e negativo) representam o valor da função naqueles intervalos (x>r e x<r).
a < 0: Função decrescente.
Na função decrescente, quanto maior for o valor de x, menor será o valor de y (ou f(x)), ou seja, o valor da função decresce conforme o valor da variável x aumenta. Sendo assim, a análise do sinal da função será diferente.
Vejamos a representação gráfica de uma função decrescente:

Analisando o gráfico, temos que:

Pelo dispositivo prático, temos:

Portanto, basta saber se a função é crescente ou decrescente, fato este determinado pelo sinal do coeficiente a, e depois determinar o zero da função. Com isso o estudo do sinal fica fácil.
Compreender esse estudo dos sinais é importante não apenas para as funções no geral, mas também para a determinação do conjunto solução das inequações.