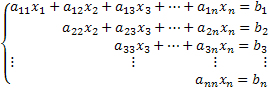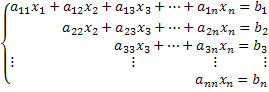Escalonar sistemas consiste em um método para classificar, resolver e discutir sistemas lineares de qualquer ordem. Confira o artigo de Classificação de sistemas lineares escalonados e Processo de escalonamento de um sistema linear.
Contudo, é necessário primeiro compreender o sistema escalonado. Exemplificando um sistema 4x4, discutiremos e compreenderemos tal sistema.
.png)
.png)
Veja que um sistema escalonado é aquele no qual, a cada equação, uma nova incógnita possui coeficiente nulo, anulando assim uma quantidade considerável de incógnitas no sistema. Obtendo um sistema escalonado desta forma, obtêm-se as soluções de maneira fácil. Veja no nosso exemplo genérico de um sistema 4x4 que a última linha nos fornece o valor da incógnita x4. Substituindo esse valor na terceira equação, obtém-se o valor da incógnita x3 e assim sucessivamente.
Exemplo:
.png)
Note que este é um sistema escalonado. Vejamos a solução deste sistema.
Da terceira equação temos que z = 2. Substituindo esse valor na segunda equação, teremos:
.png)
Agora que temos os valores de z e y, substituiremos tais valores na primeira equação.
.png)
Com isso, temos que este sistema é SPD (Sistema Possível Determinado), cuja solução é: (4, 1, 2).
.png)
Na segunda equação, tem-se o valor de y, portanto, basta substituí-lo na primeira equação.
.png)
.png)
Note que neste sistema, o número de equações é inferior ao número de incógnitas. Neste exemplo, temos três incógnitas e apenas duas equações. Em casos como este, podemos escrever a terceira linha, como uma equação nula. Ficando da seguinte forma:
.png)
Entretanto, nem sempre o sistema será dado previamente escalonado, para isso é preciso conhecer as técnicas de escalonamento. Portanto, confira o artigo “Processo de escalonamento de um sistema linear”.