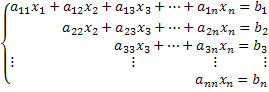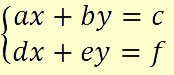Ao solucionarmos um sistema linear, obteremos um conjunto solução com valores correspondentes às incógnitas deste sistema. Diremos que um sistema é equivalente a outro, quando este conjunto solução for igual, ou seja, quando estes sistemas possuírem o mesmo conjunto solução.
Exemplo:
.png)
Então, para verificarmos se um sistema linear é equivalente a outro, basta encontrarmos o conjunto solução de ambos, e verificarmos se estes são iguais.
Verifique se os sistemas a seguir são equivalentes:

Conhecendo o conjunto solução de um dos sistemas, teremos que encontrar o outro conjunto solução e verificar se estes são iguais.
Solucionando o sistema I.
.png)
.png)
Substituindo o valor de x em uma das equações, encontraremos o valor de y.
.png)
Dessa forma, o conjunto solução deste sistema é:
.png)
Também podemos resolver sistemas a fim de encontrarmos parâmetros que indiquem dois sistemas equivalentes.
Exemplo: Quais devem ser os valores para a e b, para que os sistemas sejam equivalentes?

Desenvolvendo o primeiro sistema, teremos o conjunto solução S={(12,8)}, se quisermos obter sistemas equivalentes, este deverá ser o conjunto solução do segundo sistema. Para encontrarmos os valores dos coeficientes a e b, basta substituirmos os valores de x e y no sistema, e encontrarmos os valores de a e b em cada equação.