Equação polinomial

As equações polinomiais são bastante recorrentes em problemas envolvendo a matemática. É por meio da equação que buscamos encontrar valores desconhecidos de determinadas situações. Conhecemos como equação polinomial qualquer equação que envolva um polinômio.

Para encontrarmos as possíveis soluções de uma equação polinomial, é necessário conhecermos o grau desse polinômio. Conhecendo o grau do polinômio, para cada caso, existem métodos específicos para encontrarmos as soluções, mas nosso maior interesse é na resolução de equações polinomiais de 1º grau e de 2º grau.

De acordo com o grau desse polinômio, pelo teorema fundamental da álgebra, é possível sabermos quantas soluções complexas existem para aquela equação. Quanto maior o grau do polinômio, mais difícil será resolver a equação.

Leia também: Quais as diferenças entre função e equação?

Tópicos deste artigo

• 1 - O que é uma equação polinomial?
• 2 - Como resolver uma equação polinomial
  • Equação polinomial do 1º grau
  • Equação polinomial do 2º grau
• 3 - Teorema fundamental da álgebra
• 4 - Exercícios resolvidos:

O que é uma equação polinomial?

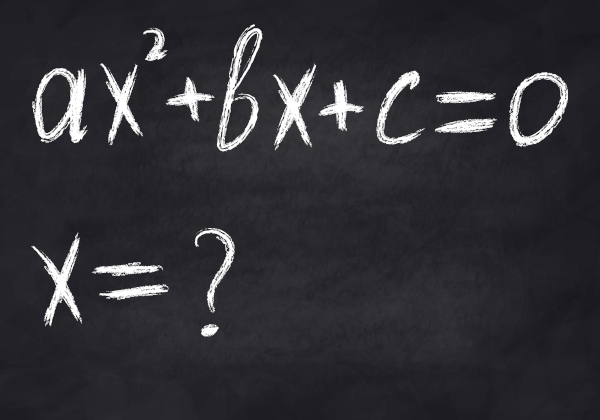
Conhecemos como uma equação polinomial a equação em que P(x) = 0 — em que P(x) é um polinômio qualquer: P(x) = a_n xⁿ + a_n-1 x^n-1 + … + a₂ x² + a₁ x¹ + a₀. Então, de forma geral, uma equação polinomial pode ser representada por:

a_n xⁿ + a_n-1 x^n-1 + … + a₂ x² + a₁ x¹ + a₀ = 0

Exemplos:

• 2x² + 5x – 2 = 0

• -x³ + 2x² – 8x + 2 = 0

• 4y³ + 2y – 2 = 0

Como resolver uma equação polinomial

Nos problemas envolvendo uma equação polinomial, o método de resolução depende do grau do polinômio. Os problemas relacionados aos conteúdos aprendidos no Ensino Médio, e também para os vestibulares e Enem, trazem dois casos de equações, a equação polinomial do 1º grau e a equação polinomial do 2º grau.

• Equação polinomial do 1º grau

Definimos como equação polinomial do primeiro grau a que pode ser descrita por ax + b = 0, em que a e b são números reais. Ela recebe esse nome porque o polinômio possui grau 1, já que esse é o maior expoente de x nesse caso. Para resolver equações do primeiro grau, vamos utilizar as quatro operações básicas a fim de encontrarmos o valor que satisfaz.

Exemplo 1:

Resolva a equação 4x – 8 = 0.

Para encontrar a solução dessa equação, vamos utilizar as operações básicas a fim de isolar a incógnita x. Como é uma igualdade, o que é feito de um lado deve ser feito do outro lado.

Conhecemos como 1º membro da equação o que está à esquerda do sinal de igual, nesse caso, 4x – 8, e de 2º membro da equação, o que está à direita da igualdade, no caso o 0.

1º passo: vamos somar 8 dos dois lados, pois sabemos que -8 + 8 = 0. É bastante comum também a afirmação de que o 8 vai passar para o segundo membro, realizando-se a operação inversa, o que é uma forma simplificada da ideia de somar 8 dos dois lados.

4x – 8 + 8 = 0 + 8

4x = 8

2º passo: note que conhecemos o valor de 4x, logo, vamos dividir por 4 dos dois lados, para encontrarmos o valor de x. Dividir por 4 dos dois lados é o mesmo que “passar o 4 dividindo”.

Encontrar o valor x = 2 significa que 2 é o valor que faz com que a equação seja verdadeira. Ao substituirmos o valor de x = 2, encontraremos uma igualdade verdadeira:

4x – 8 = 0

x = 2

4 · 2 – 8 = 0

8 – 8 = 0

0 = 0

O que mostra que 2 é a solução da equação.

Veja também: Como simplificar frações algébricas?

• Equação polinomial do 2º grau

Para encontrarmos a solução de uma equação polinomial do 2º grau, conhecida também como equação quadrática, utilizamos o método conhecido como fórmula de Bhaskara — o mais utilizado para resolver equações do 2º grau.

Uma equação polinomial do 2º grau é do tipo ax² + bx + c = 0. Para encontrarmos os valores que fazem com que essa equação seja verdadeira, é necessário calcularmos o delta (Δ) e encontrarmos x₁ e x₂ com a fórmula de Bhaskara:

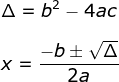
Exemplo 2:

Encontre o conjunto de soluções da equação x² – 4x + 3 = 0.

Para encontrar a solução da equação, primeiro identificamos os coeficientes a, b e c.

a → sempre acompanha o termo x², nesse caso, a = 1.

b → sempre acompanha o termo x, nesse caso, b= -4.

c → é sempre o termo independente, ou seja, não acompanha nenhuma incógnita, nesse caso, c = 3.

Então, para calcular o delta, temos que:

a = 1

b = -4

c = 3

Δ = b² – 4 · a · c

Δ = (-4)² – 4 · 1 · 3

Δ = 16 – 12

Δ = 4

Conhecendo o valor de Δ, vamos encontrar os valores de x que satisfazem a equação por meio da fórmula de Bhaskara:

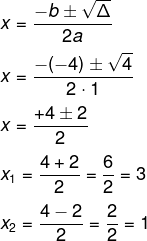
As soluções da equação são 3 e 1. Ao substituirmos qualquer um desses valores no lugar da variável x, isso faz com que a equação seja verdadeira. Para saber mais sobre esse tipo de equação polinomial, leia: Equação do 2º grau.

Teorema fundamental da álgebra

Um dos teoremas mais importantes da álgebra, o teorema fundamental da álgebra (TFA), diz que: dado um polinômio de única variável e grau n, a quantidade de raízes complexas, ou seja, valores que fazem com que P(x) seja igual a 0, também será igual a n.

É possível perceber isso quando analisamos uma equação polinomial do primeiro grau e sabemos que ela possui uma única solução, porém, quando trabalhamos com equações do 2º grau, haverá duas soluções, e assim sucessivamente.

Fatoração

Conhecendo as soluções da equação polinomial, é possível reescrevermos o polinômio de forma fatorada, seja P(x) = a_n xⁿ + a_n-1 x^n-1 + … + a₂ x² + a₁ x¹ + a₀, com raízes complexas iguais a x₁, x₂, x₃, x₄ … x_n. Então podemos reescrever o polinômio em sua forma fatorada da seguinte maneira:

P(x) = a_n(x – x₁) (x – x₂) (x – x₃) …. (x – x_n-1) (x – x_n)

Exemplo:

Escreva a forma fatorada do polinômio P(x) = x² – 4x + 3.

Como resolvemos essa equação no exemplo 2, encontramos como raízes x₁ = 1 e x₂ = 3, e também temos que a = 1, então, na forma fatorada, temos que:

P(x) = 1(x – 1) (x – 3)

Em alguns casos, é possível que uma mesma raiz apareça mais de uma vez na fatoração, assim, quando uma raiz aparece n vezes na fatoração, dizemos que ela possui multiplicidade n.

Exemplo:

Encontre o polinômio de grau 3, tal que as suas raízes sejam x₁ = 5, x₂ = 5, e x₃ = -2, sabendo que o coeficiente de x³ é 3.

Primeiro vamos escrever o polinômio na forma fatorada. Note que 5 é uma raiz do polinômio de multiplicidade 2, então ele será representado da seguinte maneira:

P(x) = 3 (x – 5) (x – 5) (x - (-2))

P(x) = 3 (x – 5)² (x + 2)

Agora vamos calcular a multiplicação desses polinômios:

P(x) = 3 (x² – 10x + 25) (x + 2)

P(x) = 3 (x³ – 10x² + 25x + 2x² – 20x + 50)

Simplificando o polinômio, teremos:

P(x) = 3 (x³ – 8x² + 5x + 50)

P(x) = 3x³ – 24x² + 15x + 150

Exercícios resolvidos:

Questão 1 – (Enem) O Salto Triplo é uma modalidade do atletismo em que o atleta dá um salto em um só pé, uma passada e um salto, nessa ordem. Sendo que o salto com impulsão em um só pé será feito de modo que o atleta caia primeiro sobre o mesmo pé que deu a impulsão; na passada ele cairá com o outro pé, do qual o salto é realizado.

Um atleta da modalidade Salto Triplo, depois de estudar seus movimentos, percebeu que, do segundo para o primeiro salto, o alcance diminuía em 1,2 m, e, do terceiro para o segundo salto, o alcance diminuía 1,5 m. Querendo atingir a meta de 17,4 m nessa prova e considerando os seus estudos, a distância alcançada no primeiro salto teria de estar entre

A) 4,0 m e 5,0 m.

B) 5,0 m e 6,0 m.

C) 6,0 m e 7,0 m.

D) 7,0 m e 8,0 m.

E) 8,0 m e 9,0 m.

Resolução

Alternativa D.

Sabendo que o atleta deu três saltos, temos que x é o alcance do primeiro salto. Como ele perde 1,2 m de alcance do primeiro para o segundo salto, então o segundo salto é x – 1,2, e, por fim, como do terceiro para o segundo salto ele perde 1,5 m, então o terceiro salto será x – 1,2 – 1,5. Assim teremos:

Alcance dos saltos:

1º salto → x

2º salto → x – 1,2

3º salto → x – 1,2 – 1,5 = x – 2,7

A soma do alcance dos três altos precisa ser igual a 17,4 m, logo, a soma dos três saltos tem que ser igual a 17,4: entre 7,0 e 8,0 metros.

Questão 2 – (Enem 2016) Para evitar uma epidemia, a Secretaria de Saúde de uma cidade dedetizou todos os bairros, de modo a evitar a proliferação do mosquito da dengue. Sabe-se que o número f de infectados é dado pela função f(t) = -2t² + 120t (em que t é expresso em dia e t = 0 é o dia anterior à primeira infecção) e que tal expressão é válida para os 60 primeiros dias da epidemia.

A Secretaria de Saúde decidiu que uma segunda dedetização deveria ser feita no dia em que o número de infectados chegasse à marca de 1 600 pessoas, e uma segunda dedetização precisou acontecer.

A segunda dedetização começou no:

A) 19º dia.

B) 20º dia.

C) 29º dia.

D) 30º dia.

E) 60º dia.

Resolução

Alternativa B.

Queremos resolver a equação:

-2t² + 120t = 1600

Igualando a 0, teremos uma equação do 2º grau completa:

-2t² + 120t – 1600 = 0

Agora vamos calcular o valor de Δ:

a = -2

b = 120

c = -1600

Δ = b² – 4ac

Δ = 120² – 4 (-2) (1600)

Δ = 14400 – 12800

Δ = 1600

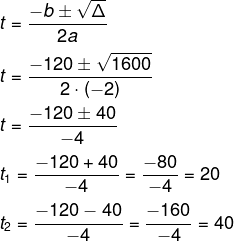
No 20º dia, teremos 1600 infectados pela primeira vez.