Equação modular é aquela que possui pelo menos uma incógnita dentro do módulo. Para representar o módulo de um número, escrevemos esse número n na forma | n |. O módulo de um número real é conhecido também como valor absoluto e representa a distância a que um número se encontra de zero quando representado em uma reta. Sendo assim, o seu valor é sempre positivo.
Para resolver a equação modular, é necessário analisar os dois casos possíveis para o módulo: quando o valor no módulo é negativo e quando o valor no módulo é positivo. Logo, uma equação modular pode ter mais de uma solução. Para resolver esse tipo de equação, é fundamental o domínio das propriedades do módulo.
Saiba mais: O que é inequação modular?
Tópicos deste artigo
- 1 - Resumo sobre equação modular
- 2 - Videoaula sobre equações modulares
- 3 - O que é uma equação modular?
- 4 - O que é módulo de um número real?
- 5 - Como resolver uma equação modular?
- 6 - Exercícios resolvidos sobre equação modular
Resumo sobre equação modular
-
Equação modular é toda equação que possui uma ou mais variáveis dentro de um módulo.
-
O módulo de um número também é conhecido como valor absoluto e é sempre um número positivo.
-
Dado um número real n, sabemos que:
![]()
Videoaula sobre equações modulares
O que é uma equação modular?
A equação modular é qualquer equação que possui incógnita dentro do módulo. Veja alguns exemplos a seguir:
-
\(3x–4∨1\)
-
\(x^2+5x–6∨0\)
-
\(2x\vee–5=3x\)
Para aprender como resolver uma equação modular, é importante, de início, compreender o que é o módulo de um número real.
O que é módulo de um número real?
Conhecemos como módulo de um número real ou valor absoluto a distância a que um número se encontra de zero quando representado em uma reta. Essa distância é sempre positiva, sendo assim, o módulo é sempre um número positivo.
![]()
Exemplos:
-
\(3\vee3\)
-
\(\left|-3\right|=-\left(-3\right)=3\)
-
\(\left|\sqrt5\right|=\sqrt5\)
-
\(\left|-\sqrt3\right|=\sqrt3\)
Leia também: Equação exponencial — a equação que possui incógnitas no expoente
Como resolver uma equação modular?
Para encontrar o conjunto de soluções de uma equação modular, aplicamos na equação a definição de módulo, ou seja, analisamos quando a expressão dentro do módulo é maior que zero e quando a expressão dentro do módulo é menor que zero.
→ Exemplos de resolução de uma equação modular
- Exemplo 1:
Encontre o conjunto de soluções da equação:
\(x\vee3\)
Resolução:
Para eliminar o módulo, vamos analisar os dois casos possíveis:
Primeiro caso
Se:
\(x\geq0\)
Então:
\(\left|x\right|=x\)
Logo, temos que:
\(x =3\)
Segundo caso
Se:
\(x<0\)
Então:
\(\left|x\right|=-x\)
Logo, temos que:
\(-x=3\)\(\rightarrow\)\(x=-3\)
As soluções são, portanto, \(x=3\) ou \(x=-3\).
- Exemplo 2:
Encontre o conjunto de soluções da equação:
\(2x–6∨4\)
Resolução:
Primeiro caso
Se:
\(2x-6\geq0\)
Então:
\(\left|2x-6\right|=2x-6\),
Logo, temos que:
\(2x-6=4\)
Agora, basta utilizarmos as técnicas de resolução de equação:
\(2x=4+6\)
\(2x=10\)
\(x=\frac{10}{2}\)
\(x=5\)
Segundo caso
Se:
\(2x-6<0\)
Então:
\(\left|2x-6\right|=-\left(2x-6\right)\)
Logo, temos que:
\(-\left(2x-6\right)=4\cdot\left(-1\right)\)
\(2x-6=-4\)
\(2x=-4+6\)
\(2x=2\)
\(x=\frac{2}{2}\)
\(x=1\)
As soluções dessa equação modular são, portanto, \(x=1\) ou \(x=5\).
Veja também: Como resolver uma equação do primeiro grau?
Exercícios resolvidos sobre equação modular
Questão 1
A soma das soluções da equação |2x – 1| = x + 5 é:
A) 7/6
B) – 4/3
C) 6
D) 14/3
E) – 8/3
Resolução:
Alternativa D
Analisemos cada um dos casos.
Primeiro caso
Se:
\(\left|2x-1\right|\geq0\)
Então:
\(\left|2x-1\right|=2x-1\)
Logo, temos que:
\(2x–1=x+5\)
\(2x-x=5+1\)
\(x=6\)
Segundo caso
Se:
\(\left|2x-1\right|<0\)
Então:
\(\left|2x-1\right|=-\left(2x-1\right)\)
\(-\left(2x-1\right)=x+5\)
\(-2x+1=x+5\)
\(-2x-x=5-1\)
\(-3x=4\)
\(x=\frac{-4}{3}\)
Logo, temos que:
\(\frac{-4}{3}+6=\frac{-4+18}{3}=\frac{14}{3}\)
Questão 2
(UFJF) O número de soluções negativas da equação modular |5x – 6| = x² é:
A) 0
B) 1
C) 2
D) 3
E) 4
Resolução:
Alternativa B
Há duas possibilidades:
\(5x–6=x2\) ou \(5x–6=-x2\)
Primeiro caso
\(5x-6=x^2\)
\(-x^2+5x-6=0\)
Resolvendo a equação do 2º grau, temos:
a = – 1, b = 5 c = – 6
\(\mathrm{\Delta}=b^2-4ac\)
\(\mathrm{\Delta}=5^2-4\cdot\left(-1\right)\cdot\left(-6\right)\)
\(\mathrm{\Delta}=25-24\)
\(\mathrm{\Delta}=1\)
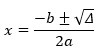
\(x=\frac{-5\pm\sqrt1}{2\cdot\left(-1\right)}\)
\(x=\frac{-5\pm1}{-2}\)
\(x_1=\frac{-5+1}{-2}\)
\(x_1=\frac{-4}{-2}\)
\(x_1=2\)
\(x_2=\frac{-5-1}{-2}\)
\(x_2=\frac{-6}{-2}\)
\(x_2=3\)
Segundo caso
\(5x–6=-x2\)
\(x^2+5x-6=0\)
Resolvendo a equação do 2º grau, temos:
a = 1, b = 5 e c = – 6
\(\mathrm{\Delta}=b^2-4ac\)
\(\mathrm{\Delta}=5^2-4\cdot1\cdot\left(-6\right)\)
\(\mathrm{\Delta}=25+24\)
\(\mathrm{\Delta}=49\)
Assim:
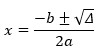
\(x=\frac{-5\pm\sqrt{49}}{2\cdot1}\)
\(x=\frac{-5\pm7}{2}\)
\(x_1=\frac{-5+7}{2}\)
\(x_1=\frac{2}{2}\)
\(x_2=\frac{-5-7}{2}\)
\(x_2=\frac{-12}{2}\)
\(x_2=-6\)
Analisando as soluções, podemos perceber que a única negativa é x = – 6, logo há 1 solução negativa.