A equação geral da reta é uma maneira algébrica de se estudar o comportamento de uma reta no plano cartesiano. Na geometria analítica, estudamos a fundo objetos da geometria plana representados no plano cartesiano. Um desses objetos é a reta, que pode ter seu comportamento descrito pela equação ax + by + c = 0, os coeficientes a, b e c são todos números reais, em que a e b são diferentes de zero.
Para encontrar a equação geral da reta, é necessário conhecer pelo menos dois pontos pertencentes a essa reta. Conhecendo os dois pontos da reta, existem dois métodos distintos para se encontrar a equação geral da reta. Além da equação geral da reta, existem outras que podem descrever esse comportamento, sendo elas a equação reduzida da reta e a equação segmentária da reta.
Leia também: O que é um par ordenado?
Tópicos deste artigo
- 1 - Passo a passo para encontrar a equação geral da reta
- 2 - Equação reduzida da reta
- 3 - Equação segmentária da reta
- 4 - Exercícios resolvidos
Passo a passo para encontrar a equação geral da reta
Para encontrarmos a equação geral da reta, existem dois métodos, um deles utiliza a equação reduzida da reta para chegar-se à equação geral, já o outro é o cálculo do determinante de ordem 3, em ambos os métodos, é necessário conhecer, pelo menos, dois pontos da reta.
Antes de compreender como encontrar a equação da reta geral, veja alguns exemplos.
Exemplo de equação geral da reta:
a) – 3x + 4y + 7 = 0
b) x + y – 3 = 0
c) 2x – 5y = 0
Então, para encontrar a equação geral de uma reta, é necessário conhecer dois pontos dessa reta. Seja A(xA, yA) e B(xB, yB) dois pontos pertencentes à reta cujos valores das coordenadas são conhecidos, para encontrar a equação geral da reta, podemos seguir alguns passos ao definirmos o método que será utilizado.
-
Método 1
Para encontrar a equação geral da reta, utilizaremos duas fórmulas:
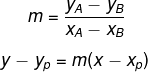
Em que (xp, yp) é um dos pontos que conhecemos.
Exemplo:
A(2,1) e B(5,7)
1º passo: encontrar o coeficiente angular m.
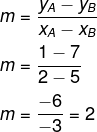
2º passo: escolher um dos pontos e substituir os valores de m e desse ponto na equação, igualando-a a zero.
y – yp = m (x – xp)
Sabendo que m = 2, e escolhendo o ponto A(2,1), temos que:
y – 1 = 2 (x – 2)
y – 1 = 2x – 4
y – 2x – 1 + 4 = 0
– 2x + y + 3 = 0 → equação geral da reta r.
Veja também: Como calcular a distância entre dois pontos no espaço?
-
Método 2
Vamos construir a matriz com os dois pontos que conhecemos: os valores A(xA, yA), B(xB, yB) e um ponto arbitrário, e C (x,y).
1º passo: montar a matriz.
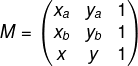
2º passo: resolver a equação det(M) = 0.
Para que os pontos estejam alinhados, o valor do determinante da matriz tem que ser igual a zero, por isso, igualamos o determinante da matriz M a zero.
Exemplo:
Utilizando os pontos do exemplo anterior, encontraremos a equação geral da reta.
A(2,1), B(5,7) e C(x,y)
Primeiro vamos montar a matriz:
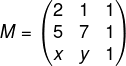
Agora calcularemos o seu determinante:
det(M) = 14 + x + 5y – 7x – 5 – 2y = 0
det(M) = 3y – 5x + 9 = 0
Note que essa é a equação de uma reta, sendo assim, a equação geral da reta que passa pelos pontos A, B e C é – 5x + 3y + 9 = 0.
Equação reduzida da reta
Outra forma de representar a equação da reta é a equação reduzida. A diferença da equação geral para a equação reduzida é que, na equação geral, o segundo membro é sempre igual a zero, agora, na equação reduzida, vamos sempre isolar o y no primeiro membro. A equação reduzida da reta é sempre descrita por y = mx + n, em que m e n são números reais, com m diferente de zero.
Conhecendo a equação geral da reta, é possível encontrar a reduzida apenas isolando o y.
Exemplo:
– 5x + 3y + 9 = 0
Vamos isolar o y no primeiro membro:
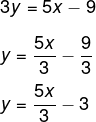
Toda reta pode ser representada por uma equação geral e por uma equação reduzida. Muitas vezes a equação reduzida é mais interessante. Já que o m é conhecido como coeficiente angular, com base nele é possível obter-se informações importantes da reta, pois seu valor traz informações sobre a inclinação dela. Já o n é o coeficiente linear, que é o ponto no plano cartesiano em que a reta corta o eixo y.
Equação segmentária da reta
Assim como a equação geral e a equação reduzida da reta, a equação segmentária é uma maneira de representar a equação da reta. A equação segmentária tem esse nome porque ela nos informa os pontos em que a reta intercepta os eixos x e y. A equação segmentária da reta é descrita por:
![]()
Exemplo:
Encontre a equação segmentária da reta -5x + 3y – 9 = 0.
Vamos isolar o termo independente 9 no segundo membro:
-5x + 3y = 9
Agora vamos dividir toda a equação por 9:
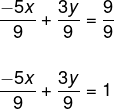
Agora vamos reescrever cada um dos termos colocando c/a e c/b.
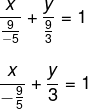
Acesse também: Qual é a equação geral da circunferência?
Exercícios resolvidos
Questão 1 – A representação da equação 4x – 2y – 6 = 0, em sua forma reduzida, é:
A) y = 2x – 3
B) y = -2x + 3
C) y = 2x + 3
D) y = -2x – 3
E) 2y = 4x – 6
Resolução
Alternativa A
Primeiro vamos isolar o y:
-2y = -4x + 6, como o coeficiente de y é negativo, multiplicaremos a equação por -1.
2y = 4x – 6, dividindo todos os termos por 2, encontraremos a equação reduzida.
y = 2x – 3
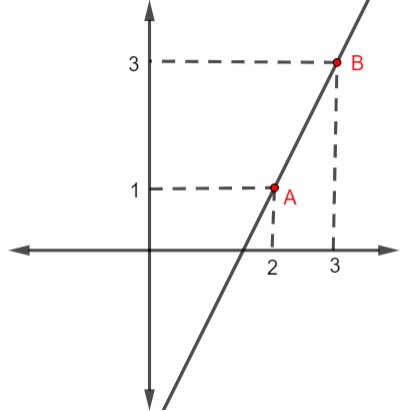
Questão 2 – A equação geral da reta representada no plano cartesiano é:
A) 2x + 2y – 6 = 0
B) x + y – 9 = 0
C) 2x – y + 3 = 0
D) -2x + y + 3 = 0
E) x + 2y – 3 = 0
Resolução
Alternativa D
Primeiro vamos identificar os dois pontos, são eles A(2,1) e B(3,3). Seja P(x,y) um ponto qualquer da reta, devemos calcular o determinante da matriz M e igualar a zero, colocando em cada linha o valor de x, y e 1.
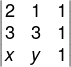
det(M) = 6 + x + 3y – 3x – 3 – 2y = 0
det(M) = -2x + y + 3 = 0