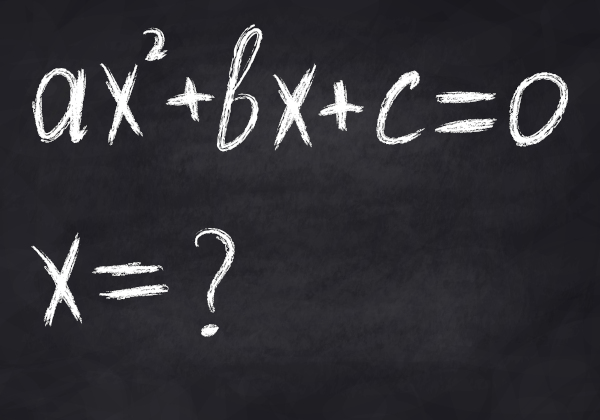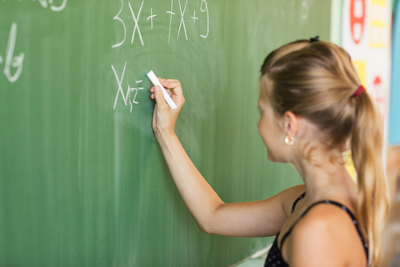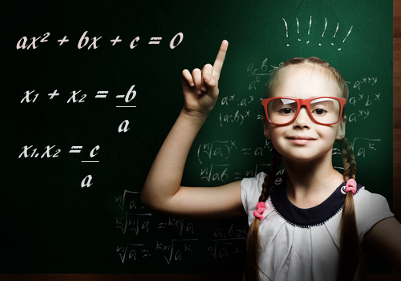Situações-problema que envolvem uma equação do 2º grau são bastante comuns na Matemática, Física e Química. Definimos como equação do 2º grau a equação ax² +bx +c = 0, em que a, b e c são números reais e a ≠0.
De modo geral, existem equações do 2º completas e incompletas, que são resolvidas pela fórmula de Bhaskara ou por soma e produto. Vale dizer que as equações do 2º grau incompletas possuem métodos específicos de resolução, que, algumas vezes, são mais convenientes do que utilizar Bhaskara ou soma e produto.
Leia também: Quais as diferenças entre função e equação?
Tópicos deste artigo
- 1 - O que são equações do segundo grau?
- 2 - Tipos de equações do 2º grau
- 3 - Como resolver equações do 2º grau?
- 4 - Equações incompletas
- 5 - Sistema de equações do segundo grau
- 6 - Exercícios resolvidos sobre equação do 2º grau
O que são equações do segundo grau?
Definimos como equação do 2º grau ou equações quadráticas qualquer equação do tipo ax² + bx + c = 0 em que a, b e c são números reais e a ≠ 0. Ela recebe esse nome porque, no primeiro membro da igualdade, há um polinômio de grau dois com uma única incógnita. Note que, dos coeficientes a, b e c, somente o a é diferente de zero, pois, caso ele fosse igual a zero, o termo ax² seria igual a zero, logo a equação se tornaria uma equação do primeiro grau: bx + c = 0.
Independentemente da ordem da equação, o coeficiente a sempre acompanha o termo x², o coeficiente b sempre acompanha o termo x, e o coeficiente c é sempre o termo independente.
Confira alguns exemplos de equações do 2º grau:
a) 2x² – 3x + 4 = 0 → a = 2; b= – 3; c = 4
b) - x ² + 5x – 1 = 0 → a = -1; b =5; c = –1
c) 5x² = 0 → a = 5; b = 0; c = 0
d) x² – 2 = 0 → a = 1 b = 0; c = –2
e) -3x² + 0,2x = 0 → a= – 3; b= 0,2; c = 0
Tipos de equações do 2º grau
Existem dois tipos de equações do 2º grau: as que são completas e as que são incompletas. Uma equação é conhecida como completa quando ela possui todos os seus coeficientes diferentes de zero, como os exemplos (a) e (b) apresentados anteriormente. Quando pelo menos um de seus coeficientes é igual a zero, a equação é conhecida como incompleta, como nos exemplos (c), (d) e (e).
Exemplos:
-
2x² + 3x – 4 = 0 → Completa
-
9x² – 2 = 0 → Incompleta
Veja também: Como resolver problemas envolvendo equações?
Como resolver equações do 2º grau?
Conhecemos como soluções ou raízes da equação ax² + bx + c = 0 os valores de x que fazem com que essa equação seja verdadeira. Uma equação do 2º grau pode ter no máximo dois números reais que sejam raízes dela. Para resolver equações do 2º grau completas, existem dois métodos mais comuns:
-
fórmula de Bhaskara;
-
soma e produto.
O primeiro método é bastante mecânico, o que faz com que muitos o prefiram. Já para utilizar o segundo, é necessário o conhecimento de múltiplos e divisores. Além disso, quando as soluções da equação são números quebrados, soma e produto não é uma alternativa boa.
-
Fórmula de Bhaskara
Para encontrar a solução de uma equação do 2º grau utilizando a fórmula de Bhaskara, precisamos conhecer duas fórmulas: uma delas é a do delta (Δ), conhecido também como discriminante, e a outra é a fórmula de Bhaskara.
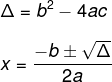
Nem sempre a equação possui solução real. O valor do Δ é que nos indica isso, existindo três possibilidades.
-
Se Δ > 0, então a equação possui duas soluções reais.
-
Se Δ = 0, então a equação possui uma única solução real.
-
Se Δ < 0, então a equação não possui solução real.
Exemplo:
Encontre as raízes da equação x² + 2x – 3 = 0.
1º passo: encontrar os valores dos coeficientes a, b e c.
-
a = 1
-
b= 2
-
c= –3
2º passo: calcular o delta por meio da substituição do valor dos coeficientes na fórmula.
Δ = b² – 4 ac
Δ = 2² – 4· 1 ·(– 3)
Δ = 2² – 4· 1 ·(– 3)
Δ = 4 – 4 ·(– 3)
Δ = 4 + 12
Δ = 16
Como Δ > 0, então essa equação terá duas soluções reais.
3º passo: usar a fórmula de Bhaskara, substituindo as letras pelos valores da equação dos coeficientes e de delta.
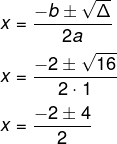
Nesse momento, é necessário dividir as duas soluções: uma será a soma e a outra será a diferença.
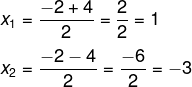
Então as possíveis soluções para essa equação são x = 1 ou x = – 3.
Acesse também: Bhaskara: resolvendo uma equação completa do 2° grau
-
Soma e produto
Nesse método é importante conhecer os divisores de um número. Ele se torna interessante quando as raízes da equação são números inteiros, porém, quando são um número decimal, esse método fica bastante complicado.
A soma e o produto é uma relação entre as raízes x1 e x2 da equação do segundo grau, logo devemos buscar quais são os possíveis valores para as raízes que satisfazem a seguinte relação:
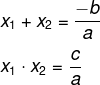
Exemplo:
Encontre as soluções para a equação x² – 5x + 6 = 0.
1º passo: encontrar a, b e c.
a = 1
b = -5
c = 6
2º passo: substituir os valores de a, b e c na fórmula.
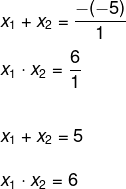
3º passo: encontrar o valor de x1 e x2 analisando a equação.
Nesse caso, estamos procurando dois números cujo produto seja igual a 6 e a soma seja igual a 5.
Os números cuja multiplicação é igual a 6 são:
I. 6 x 1 = 6
II. 3 x 2 =6
III. (-6) x (-1) = 6
IV. (-3) x (-2) = 6
Dos possíveis resultados, vamos buscar aquele em que a soma seja igual a 5. Note que somente a II possui soma igual a 5, logo as raízes da equação são x1=3 e x2=2.
Leia também: Soma e produto das raízes de uma equação do 2º grau
Equações incompletas
Existem três possibilidades de equação incompleta. Para cada uma delas, é possível realizar a resolução por soma e produto ou também pela fórmula de Bhaskara, porém cada uma delas possui uma terceira forma, geralmente com resolução mais rápida.
-
Equações incompletas do tipo ax² = 0
Nesse caso não há muito o que ser feito, já que b = 0 e c = 0. Aplicar qualquer um dos métodos anteriores seria bastante demorado. Então, basta isolarmos o x.
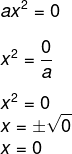
Logo, para qualquer valor de a — lembrando que, por definição, a é diferente de zero —, o valor de x sempre será 0.
-
Equações incompletas do tipo ax² + bx =0
Nesse caso, quando somente c = 0, é possível colocar o x em evidência na equação, gerando o seguinte produto:
x(ax +b) = 0
Para que uma multiplicação seja igual a zero, um dos seus termos precisa ser zero, logo as possibilidades são:
x= 0 ou ax+b = 0
Uma das soluções é x = 0, e a outra é uma equação do primeiro grau, que podemos resolver isolando o x.
Exemplo:
2x² + 3x = 0
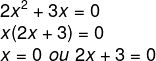
Encontramos uma solução x1 = 0. Isolando x na segunda equação, temos que:
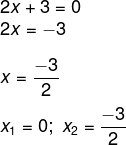
-
Equações incompletas do tipo ax² + c =0
Nesse caso é possível resolver isolando a incógnita, já que o termo c é independente, ou seja, não acompanha nenhuma incógnita. É necessário o domínio de equação do 1º grau nesse caso.
Exemplo:
3x² – 12 = 0
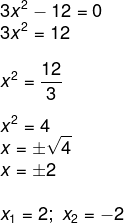
Sistema de equações do segundo grau
Resolver sistemas de equação do segundo grau exige que você tenha domínio da resolução de um sistema de equações do primeiro grau. Nesse caso, é essencial o domínio do método da adição e do método de substituição.
Exemplo:
![]()
1º passo: isolar uma das incógnitas na equação do primeiro grau.
Note que a equação II é do primeiro grau, logo reescreveremos isolando o y.
y = 1 – x
2º passo: substituir y na primeira equação.
x² + y² = 5
x² + (1 – x)² = 5
x² + 1 – 2x +x² = 5
2x² – 2x + 1 =5
Note que estamos encontrando uma equação do 2º grau, então vamos igualar a equação a zero.
2x² – 2x + 1 – 5 = 0
2x² – 2x – 4 = 0
Tendo a equação do 2º grau, vamos resolver utilizando soma e produto, mas Bhaskara também seria eficiente nesse caso.
-
a = 2
-
b = -2
-
c = -4
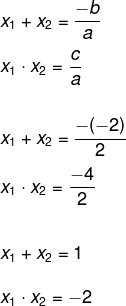
Os possíveis números cujo produto é igual a -2 são:
A. 1 x (-2) = - 2
B. (-1) x 2 = - 2
Dos resultados possíveis, queremos aquele que a soma seja igual a 1, logo o resultado B é a solução da equação.
x1 = -1 e x2 = 2
3º passo: conhecendo o valor de x, vamos encontrar os possíveis valores para y substituindo cada um deles na equação x + y = 1.
x+ y = 1
x = -1
-1 + y = 1
y = 1+1 = 2
O par ( -1, 2) é a solução do sistema de equação.
Agora faremos o seguinte:
x+ y = 1
x = 2
2+y =1
y = 1 – 2
y = -1
O par (2, -1) também é solução do sistema.
As possíveis soluções do sistema são S { (2, -1); (-1, 2)}.
Veja também: Equações biquadradas – equações de quarto grau que possuem resolução específica
Exercícios resolvidos sobre equação do 2º grau
Questão 1 – (Fuvest - adaptada) Se m e n são raízes de x² -6x +10 = 0, então a soma do inverso de m com o inverso de n é igual a?
A) 6
B) 2
C) 1
D) 3/5
E) 1/6
Resolução
Alternativa D.
Primeiro vamos encontrar o valor de m e n. Para isso, temos a equação x² – 6x + 10 = 0.
a =1
b = -6
c = 10
Utilizando soma e produto, temos que:
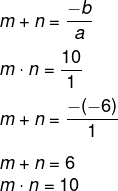
Logo, a soma do inverso de m e de n pode ser resolvida por:
![]()
Como é conhecido o valor do numerador e do denominador, temos que:
![]()
Questão 2 - O valor de c que faça com que a equação x² +6x + c =0 tenha somente uma solução real é:
A) -9
B) 3
C) 2
D) -3
E) 9
Resolução
Alternativa E.
Para que a equação tenha somente uma solução, o Δ precisa ser igual a zero.
a = 1
b = 6
Δ = b² – 4 ac
Δ = 6² – 4· 1 c
Δ = 36 – 4c
36 – 4c = 0
36 = 4c
c = 36/4
c= 9