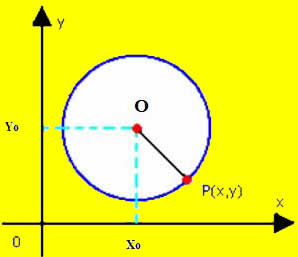
O estudo das posições relativas de uma reta em relação a uma circunferência nos mostra três possibilidades para estas posições, onde todas dependem da distância do centro da circunferência até a reta.
Para uma melhor compreensão do que será abordado neste artigo, indicamos a leitura dos artigos Distância entre ponto e reta e Posição relativa entre uma reta e uma circunferência.
Iremos encontrar a reta tangente partindo de um ponto cuja posição é de grande relevância para o estudo da reta tangente que passa por ele. Sendo assim, teremos os seguintes casos:
• Ponto P interno à circunferência (distância do centro ao ponto menor que o raio), não existe nenhuma reta tangente nestas condições;
• O ponto P como um ponto da circunferência (distância do centro ao ponto igual ao raio), nos dá uma única reta tangente, sendo P o ponto de tangência;
• Ponto P externo à circunferência (distância do centro ao ponto maior que o raio), teremos duas retas tangentes passando por este ponto.
Sendo assim, antes de irmos à busca da reta tangente, devemos verificar a posição relativa entre o ponto e a circunferência.
Vejamos um exemplo:
Determine as equações das retas tangentes à circunferência λ: x²+y²=1, traçadas pelo ponto P(√2, 0).
Devemos verificar a posição relativa à circunferência. Ou seja, calcular a distância deste ponto até o centro da circunferência.
Temos que esta circunferência possui centro C(0,0) e raio r=1. Sendo assim,
.png)
Se o ponto P é um ponto externo, podemos afirmar que devemos encontrar duas retas tangentes.
Se as retas são tangentes, sabemos que a distância do centro até a reta tangente deverá ser igual ao raio. Esta reta tangente deverá passar pelo ponto P(√2, 0).
Sendo assim, a equação da reta t será:
t: y-0=m(x-√2) -> mx-y-√2m=0
Com a equação da reta temos condições de calcular a distância do centro da circunferência até a reta tangente.
.png)
Basta substituirmos o valor do coeficiente angular m na equação da nossa reta tangente para obtermos a resposta final.
.png)
Portanto, para encontrarmos a equação de uma reta tangente traçada por um ponto dado é preciso conhecer a posição relativa deste ponto, para assim analisarmos o comportamento da reta que passa por este ponto e tangencia a circunferência.