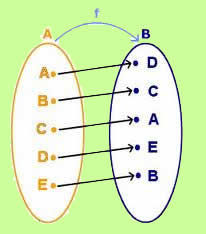
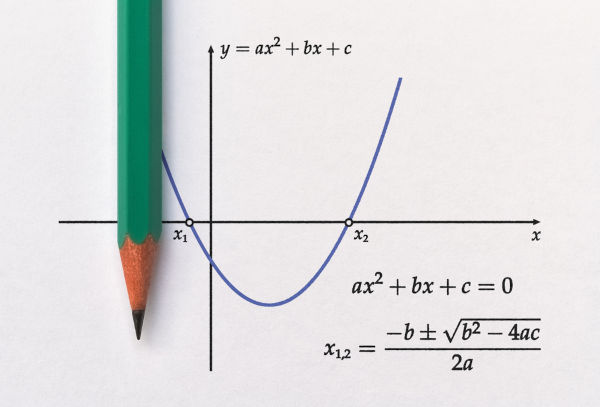
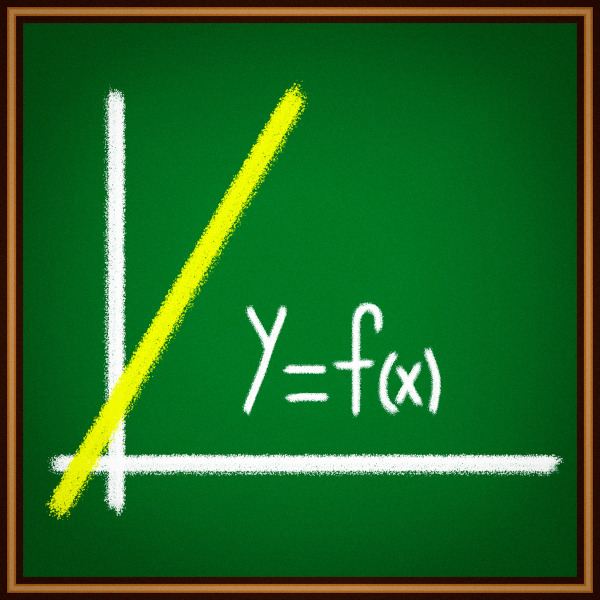
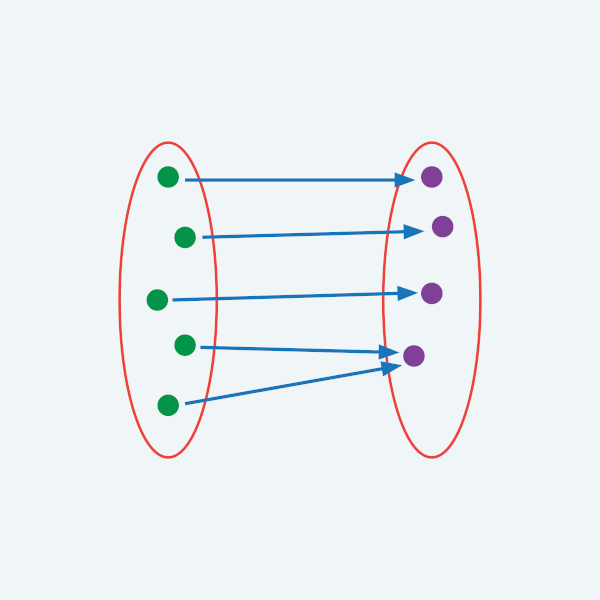
Uma função é uma regra que relaciona cada elemento de um conjunto A a um único elemento de um conjunto B. Nessa definição, o conjunto A é chamado de domínio, o conjunto B é o contradomínio, e existe ainda um subconjunto do conjunto B chamado imagem.
Uma função determina, para todo elemento x do conjunto A, qual elemento y do conjunto B está relacionado a ele. Em outras palavras, todos os elementos do conjunto A são relacionados a algum elemento do conjunto B, e para cada elemento do conjunto A existe um único “correspondente” no conjunto B.
A forma algébrica de representar a definição da função corresponde, considerados os conjuntos A e B, à regra em que a função f é:
f: A → B
y = f(x)
Observe que essa função é denominada “f”, o que pode ser feito com qualquer letra. Os símbolos A → B indicam que cada elemento do conjunto A, aplicado na função f, tem como resultado um elemento do conjunto B. É por isso que o conjunto A é chamado de domínio. Os resultados em B serão determinados a partir dos valores de A. Por esse motivo, seja x um elemento qualquer do conjunto A, x é chamado variável independente, e seja y um elemento qualquer do conjunto B, y é a variável dependente.
Domínio
Dada a função f de A em B, definida como y = f(x) (modo como deve ser lida a simbologia usada anteriormente), já sabemos que seu domínio é o conjunto A e que um elemento qualquer de A, representado pela letra x, é chamado variável independente.
O domínio é formado por todos os elementos que “dominam” os possíveis resultados encontrados para y em uma função. Esse conjunto é chamado por esse nome porque cada um dos seus valores determina um único resultado no outro conjunto.
Exemplo:
f: N → Z
y = 2x + 1
O domínio dessa função é o conjunto dos números naturais, ou seja:
N = {0, 1, 2, 3, 4, 5, …}
Portanto, esses são os valores que podem substituir a variável x na função.
Contradomínio
Dada a função f de A em B, definida como y = f(x), já sabemos que o conjunto B é chamado contradomínio. A definição de função garante que cada elemento do domínio (conjunto A) é relacionado a um único elemento do contradomínio (conjunto B). Note que a palavra “cada” garante que todos os elementos do domínio são usados em uma função, mas a expressão “um único elemento do conjunto B” não garante que todos os elementos do contradomínio serão relacionados a elementos do domínio.
Utilizando o mesmo exemplo anterior:
f: N → Z
y = 2x + 1
Note que o contradomínio dessa função é definido no conjunto dos números inteiros. Entretanto, sabemos que “2x + 1” terá como resultado apenas números ímpares. Portanto, o conjunto Z contém todos os elementos que se relacionam a elementos do domínio, não sendo necessariamente seus únicos elementos.
Imagem
O conjunto imagem é formado por todos os elementos do contradomínio que estão relacionados a algum elemento do domínio. No exemplo anterior:
f: N → Z
y = 2x + 1
Os resultados obtidos substituindo elementos do domínio na função são:
Se x = 0, y = 1
se x = 1, y = 3
se x = 2, y = 5
…
Isso significa que os valores de y sempre pertencem ao conjunto dos números ímpares não negativos. Portanto, a imagem dessa função é o conjunto dos números ímpares a partir de 1.
Cada um dos valores de y obtidos é chamado de imagem, assim, se x = 10, sua imagem é y = 21 na função dada como exemplo.