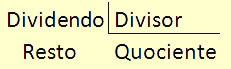Em uma divisão existem alguns termos: dividendo (número que será dividido) quociente (resultado da divisão), divisor (número que divide) e resto (o que sobra da divisão), quando o resto é igual a zero dizemos que a divisão é exata. Sendo assim, podemos concluir que nessa divisão ocorre uma divisibilidade, ou seja, podemos encontrar múltiplos e divisores.
Por exemplo, quando resolvemos a divisão 123 : 3 encontramos como quociente 41 e resto igual a 0.
Concluímos que essa divisão é exata (não sobra resto maior que zero), então dizemos que:
123 é divisível por 3, pois a divisão é exata; ou que 123 é múltiplo de 3, pois existe um número natural que multiplicado por 3 resulta em 123; ou que 3 é divisor de 123, pois existe um número que divide 123 e resulta em 3.
A partir desse exemplo podemos definir múltiplo e divisor como:
Múltiplos são resultados de uma multiplicação de dois números naturais. Por exemplo, 30 é múltiplo de 6, pois 6 x 5 = 30.
Divisores são números que dividem outros, desde que a divisão seja exata, por exemplo: 2 é divisor de 10, pois
10: 2 = 5.
Quando especificamos os múltiplos e os divisores de um número formamos conjuntos dos múltiplos e dos divisores, veja alguns exemplos de conjunto dos múltiplos e divisores de números naturais e perceba as suas particularidades.
M(5) = {0,5,10,15,20,25,30,35, ... }
M(15) = {0,15,30,45,60,75, ... }
M(10) = {0,10,20,30,40,50,60, ... }
M(2) = {0,2,4,6,8,10,12,14,16, ...}
Observando os conjuntos acima percebemos que todos eles são infinitos e que possuem um elemento em comum, o elemento 0. Como todos os conjuntos citados são formados por múltiplos de números, podemos concluir que o conjunto dos múltiplos de qualquer número sempre será infinito, pois existem infinitos números naturais que podem ser multiplicados. Podemos concluir também que sempre o 0 fará parte dos elementos de um conjuntos dos múltiplos de um número, pois qualquer número multiplicado por zero resultará em zero.
D(55) = {1,5,11,55}
D(10) = {1,2,5,10}
D(20) = {1,2,4,5,10,20}
D(200) = {1,2,4,5,8,10,20,25,40,50,100,200}
Os conjuntos dos divisores de números naturais deixam claro que todos esses conjuntos são finitos, pois não é toda divisão que o resto é igual a zero e o número 1 é divisor de qualquer número natural, pois qualquer número dividido por ele mesmo é igual a 1.
OBSERVAÇÕES:
• Quando um número é divisível por apenas um e por ele mesmo dizemos que esse número é primo.
• O único número primo par é o 2.
Aproveite para conferir nossa videoaula sobre o assunto: