A distância entre dois pontos no espaço segue o mesmo fundamento da distância entre dois pontos no plano, contudo, com uma dimensão a mais. Isso significa que a distância entre dois pontos no espaço também é o comprimento do menor segmento de reta que os liga, os pontos possuem uma coordenada “z” a mais e a fórmula para o cálculo da distância também possui mais um quadrado da diferença.
→ Fórmula: distância entre dois pontos no espaço
A fórmula para calcular a distância entre dois pontos no espaço é a seguinte:
![]()
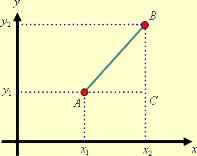
Essa fórmula é obtida da seguinte maneira: Primeiramente, desenhe uma linha reta entre os dois pontos do espaço para representar a distância entre eles.

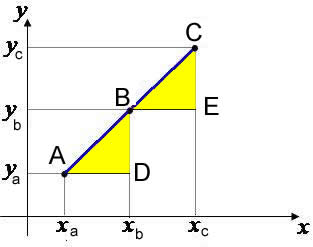
Posteriormente, desenhe a projeção do segmento sobre o plano xy:

Calcule o comprimento dessa projeção utilizando a fórmula para distância entre dois pontos:
![]()
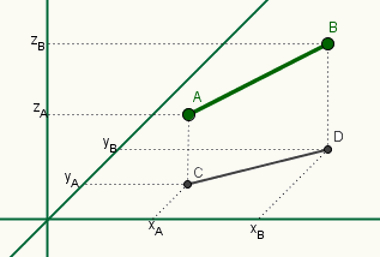
Essa é a base do triângulo retângulo cuja hipotenusa é o segmento AB. Observe isso na imagem seguinte, em perspectiva:

Para calcular o comprimento do segmento AB, basta utilizar o teorema de Pitágoras. Antes disso, porém, observe que a distância entre B e D é a diferença entre zA e zB, ou seja, dBD = (zB – zA)2. Desse modo, pelo teorema de Pitágoras, teremos a distância entre A e B:

→ Cálculo da distância entre dois pontos no espaço
Para calcular a distância entre dois pontos no espaço, basta substituir os valores numéricos de suas coordenadas na respectiva fórmula. Veja o cálculo da distância entre os pontos A = (1,2,3) e B = (-4, -5, -6).

Aproveite para conferir nossas videoaulas sobre o assunto: