A distância entre dois pontos é determinada pela Geometria Analítica, responsável por estabelecer relações entre fundamentos geométricos e algébricos. As relações são intituladas com base num sistema de coordenadas cartesianas, que é constituído de dois eixos perpendiculares enumerados.

No plano cartesiano, qualquer ponto possui uma coordenada de localização, basta identificar o ponto e observar os valores primeiramente em relação ao eixo horizontal x (abscissa) e posteriormente em relação ao eixo vertical y (ordenada).
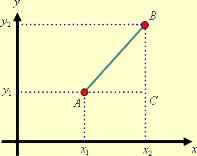
Nesse sistema de coordenadas podemos demarcar dois pontos e determinar a distância entre eles. Observe:

Observe que o triângulo formado é retângulo de catetos AC e BC e hipotenusa AB. Se aplicarmos o Teorema de Pitágoras nesse triângulo determinando a medida da hipotenusa estaremos também calculando a distância entre os pontos A e B. Vamos aplicar as propriedades da relação de Pitágoras no triângulo ABC, originando a expressão matemática responsável pela determinação da distância entre dois pontos em função de suas coordenadas.
O Teorema de Pitágoras diz: “A soma dos quadrados dos catetos é igual ao quadrado da hipotenusa”. No triângulo ABC temos que:
Cateto AC = x2 – x1
Cateto BC = y2 – y1
![]()
Exemplo 1
Qual a distância entre os pontos P(3, –3) e Q(–6, 2)?

A distância entre os pontos P e Q é igual a √106 unidades.
Exemplo 2
Determine a distância entre os pontos A(10, 20) e B(15, 6), localizados no sistema de coordenadas cartesianas.

Os pontos A e B se distanciam um do outro √221 unidades.
Aproveite para conferir nossa videoaula sobre o assunto: