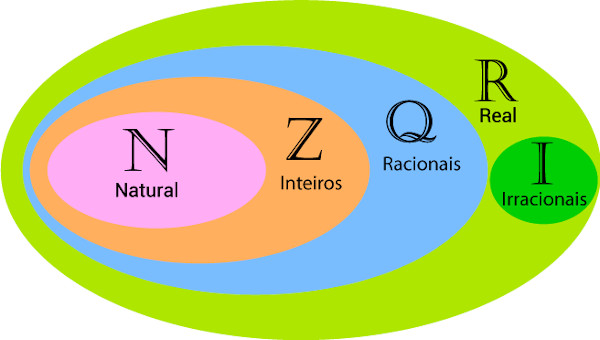
O diagrama de Venn é um método para representarmos conjuntos numéricos de forma geométrica. Essa representação facilita a visualização e realização das operações entre conjuntos. Entender a relação entre dois ou mais conjuntos é fundamental para a compreensão da teoria de conjuntos, logo, a partir do diagrama, é possível identificar a intersecção, a união e quando os conjuntos não possuem nenhum elemento em comum. A representação dos conjuntos pelo diagrama de Venn é um suporte para a resolução de problemas envolvendo conjuntos.
Leia também: Quais são os possíveis subconjuntos dos números naturais?

Tópicos deste artigo
- 1 - Relação de pertinência
- 2 - Representação de um único conjunto
- 3 - Representação de dois ou mais conjuntos
- 4 - O que significa cada uma das regiões?
- 5 - Representação de três conjuntos
- 6 - Exercícios resolvidos
Relação de pertinência
Para fazer a representação no diagrama de Venn, é fundamental compreendermos conceitos básicos de conjunto, como o que é pertinência — a relação de inclusão entre os conjuntos e as operações.
Inicialmente, dado um conjunto A, dizemos que um elemento (Є) pertence ao conjunto A se ele é desse conjunto, caso contrário, ele não pertence ao conjunto A.
Exemplo:
A = {1, 3, 5, 7, 9}

Representação de um único conjunto
Ao estudar álgebra, é fundamental que você desenvolva uma noção básica sobre conjuntos numéricos. Durante o estudo de conjuntos, é bastante comum a necessidade de analisarmos, a fundo, as relações que existem entre dois conjuntos ou mais. Para facilitar a visualização dessas relações, o diagrama de Venn é uma ferramenta de organização e representação dos conjuntos de forma geométrica.
Para representar o diagrama, precisamos saber com quantos conjuntos estamos trabalhando e se há elementos em comum entre eles ou não. Primeiro faremos a representação de um único conjunto, para isso é necessário o domínio do conceito de pertinência. Representaremos, no diagrama, os elementos que pertencem ao conjunto.
Exemplo:
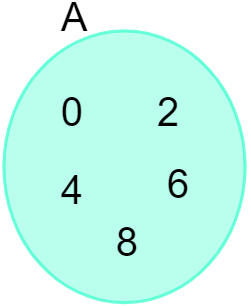
Dado o conjunto A = {0, 2, 4, 6, 8}, podemos representá-lo no diagrama a seguir:
Veja também: Introdução ao estudo dos conjuntos – conceitos básicos, operações
Representação de dois ou mais conjuntos
-
Relação de inclusão
Na busca de compreender-se a representação de dois ou mais conjuntos, é necessário o domínio da relação de inclusão e das operações entre conjuntos. Sobre a relação de inclusão, dizemos que o conjunto A está contido no conjunto B se, e somente si, todos os elementos do conjunto A pertencem ao conjunto B. Podemos dizer também que o conjunto B contém o conjunto A.
![]()
Isso significa, respectivamente, que A está contido em B e que B contém A. Independentemente da forma de representação, diz-se a mesma coisa.
Exemplo:
A = {1, 2, 3, 4} e B = {1, 2, 3, 4, 5, 6, 7}, note que todos os elementos de A também pertencem ao conjunto B, logo, podemos dizer que o conjunto A está contido no conjunto B. A representação então é feita da seguinte forma:
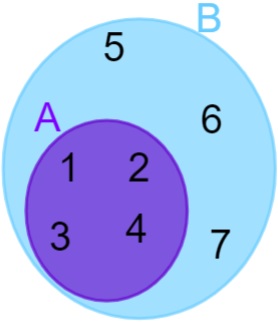
-
Conjuntos disjuntos
Também conhecidos como conjuntos mutuamente excludentes, são conjuntos numéricos que não possuem nenhum elemento em comum. Chamamos de intersecção os elementos que pertencem a dois conjuntos ao mesmo tempo, logo, para conjuntos disjuntos, a intersecção é vazia. Nesse caso a representação é bastante simples.
Exemplo:
A = {1, 2, 3, 4} e B = {5, 6, 7, 8}, note que não há nenhum elemento em comum no conjunto A e B, quando isso acontece, podemos dizer que a intersecção de A com B é vazia, representada por:
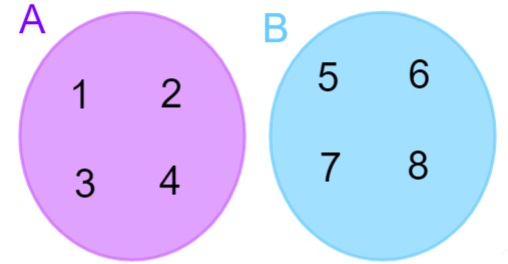
-
Quando existem elementos na intersecção
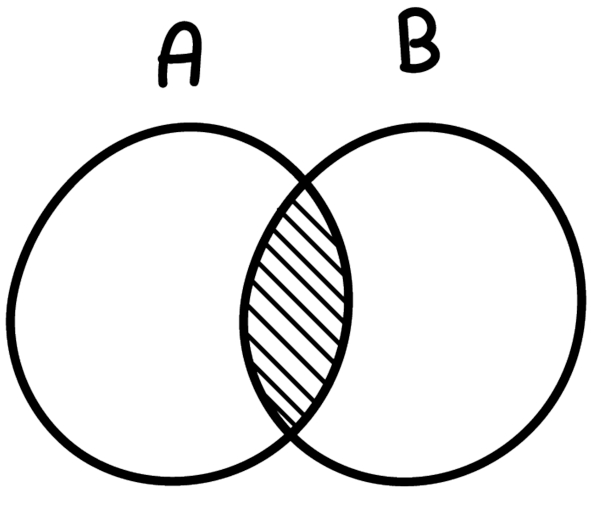
Importa, nesse caso, o domínio das operações entre esses conjuntos, o que conhecemos como intersecção de dois ou mais conjuntos. Quando existe intersecção, representamos os conjuntos com uma região em comum entre eles, essa região contém os elementos que pertencem tanto ao conjunto A quanto ao conjunto B ao mesmo tempo.
Exemplo:
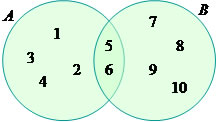
A = {1, 2, 4, 5, 6, 7} e B = {2, 3, 4, 6, 8}, note que existem alguns elementos que pertencem tanto ao conjunto A quanto ao conjunto B, o que chamamos de intersecção. Sua representação é feita da seguinte forma:
![]() –> intersecção de A com B
–> intersecção de A com B
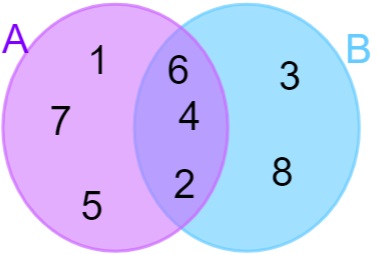
O que significa cada uma das regiões?
De forma geral, é importante a compreensão de cada uma das regiões do diagrama.
Elementos que pertencem ao conjunto A
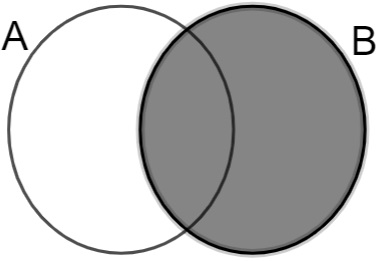
Elementos que pertencem ao conjunto B
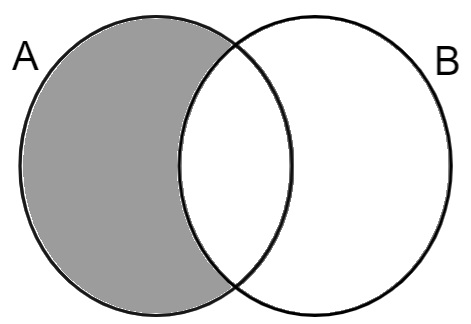
Elementos que pertencem somente ao conjunto A. Ao estudar-se operações entre conjuntos, esse conjunto é conhecido como a subtração de A – B.
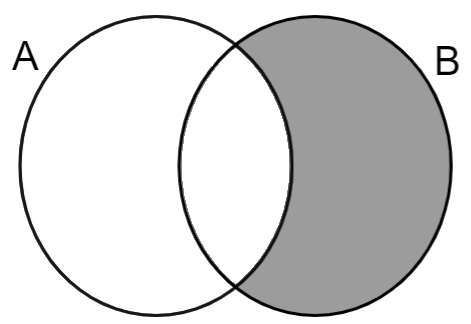
Elementos que pertencem somente ao conjunto B. Ao estudar-se operações entre conjuntos, esse conjunto é conhecido como a subtração de B – A.
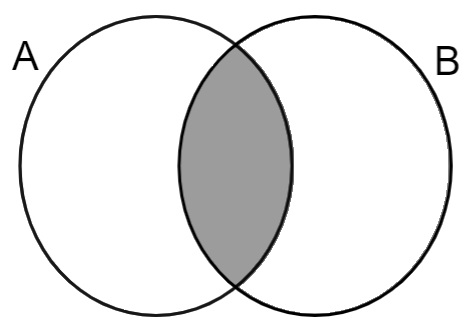
Elementos que pertencem ao conjunto A e ao conjunto B simultaneamente, ou seja, pertencem à intersecção dos conjuntos.
Acesse também: Quais são os tipos de conjuntos?
Representação de três conjuntos
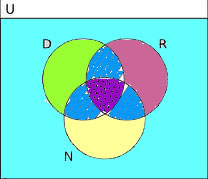
A representação de três conjuntos pode ser bastante trabalhosa, e o erro é bastante comum nesse caso. Para realizar essa representação, precisamos conhecer cada uma das regiões. Quando os conjuntos possuem intersecção, o diagrama pode ser dividido em sete regiões, conforme a imagem a seguir:
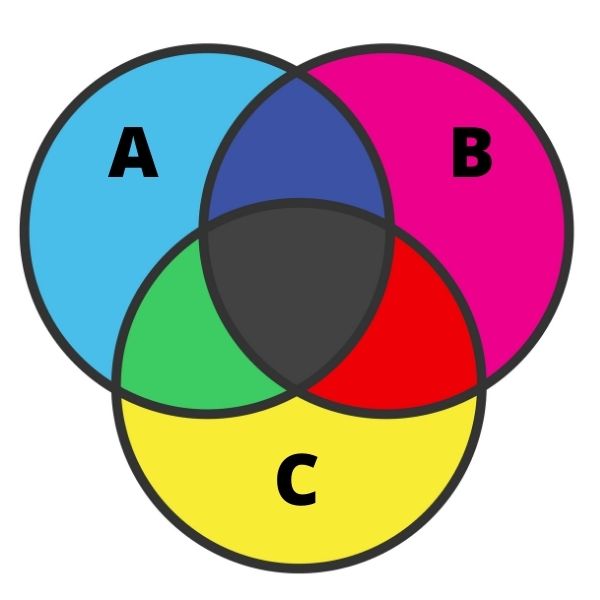
Analisando a imagem, temos em azul-claro os elementos que pertencem somente ao conjunto A. Com a mesma ideia, em rosa e em amarelo, temos, respectivamente, os elementos que pertencem somente aos conjuntos B e C.
Nas intersecções em preto, estão os elementos que pertencem aos três conjuntos simultaneamente. Na cor verde, há os elementos que pertencem somente aos conjuntos A e C; na cor vermelha, os elementos que pertencem somente aos conjuntos B e C; e, por fim, em azul-escuro, há os elementos que pertencem aos conjuntos A e B.
Exemplo:
Represente no diagrama os conjuntos a seguir:
A = {1, 2, 3, 4, 5}; B = {0, 2, 4, 6, 8}; C = {1, 2, 6, 7}
1º passo: encontrar as intersecções.
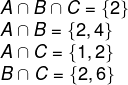
2º passo: construção do diagrama, começando pelas intersecções.
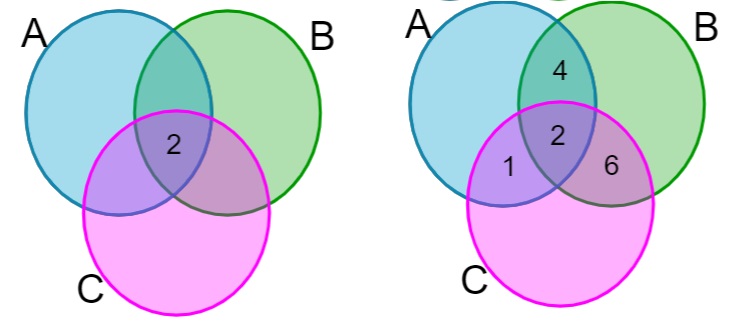
3º passo: escrever os elementos exclusivos restantes em cada um dos conjuntos.
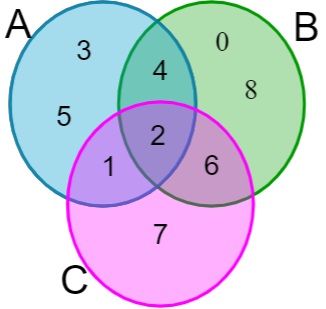
Exercícios resolvidos
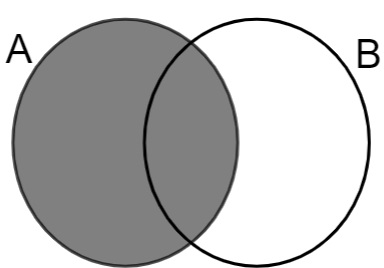
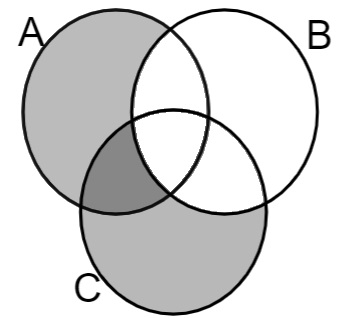
Questão 1 - Analisando-se os conjuntos A, B e C, a região pintada pode ser representada por:
a) A U B – C
b) A U C – B
c) B U C – A
d) A U B U C
Resolução
Alternativa B. Analisando a imagem, observamos que a área em branco, ou seja, retirada, é a do conjunto B, e que elementos da área pintada pertencem ao conjunto A e ao conjunto C e não ao conjunto B, logo: A U C – B.
Questão 2 - Analise o diagrama:
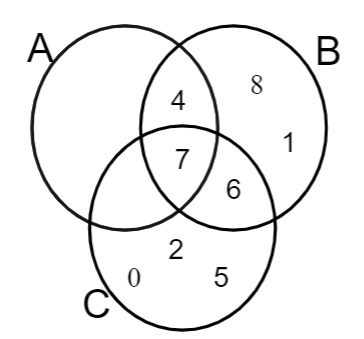
Julgue as afirmativas a seguir:
I- O conjunto A é um conjunto vazio.
II- Não existe um elemento que pertence ao conjunto A e C ao mesmo tempo.
III- O número 7 pertence a todos os conjuntos.
IV- O conjunto {0, 2, 5, 6} é composto por elementos que pertencem somente ao conjunto C.
a) Todas são falsas.
b) Somente II e III são falsas.
c) Somente I e II são falsas.
d) Somente II, III e IV são falsas.
e) Somente I, II e IV são falsas.
Resolução
Alternativa E.
I- Falsa, pois 4 e 7 pertencem ao conjunto A.
II- Falsa, pois o 7 pertence a todos os conjuntos, logo, ele pertence a A e C.
III- Verdadeira, pois 7 está na intersecção dos três conjuntos.
IV- Falsa, pois os elementos que pertencem somente a C são {0, 2, 5}. Note que o 6 está na intersecção e C com B.