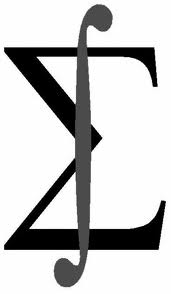Desvio-padrão

O desvio-padrão é uma medida de dispersão (ou variabilidade) muito utilizada na estatística. Essa medida caracteriza o quão próximos os dados coletados estão da média aritmética. O desvio-padrão está relacionado com o conceito de variância, outra medida de dispersão aplicada na estatística. Inclusive, o valor do desvio-padrão é obtido pela raiz quadrada da variância.

Leia também: Média ponderada — a média em que cada valor tem determinado peso

Tópicos deste artigo

• 1 - Resumo sobre desvio-padrão
• 2 - O que é desvio-padrão?
• 3 - Diferenças entre desvio-padrão e variância
• 4 - Como se calcula o desvio-padrão?
• 5 - Tipos de desvio-padrão
• 6 - Exercícios resolvidos sobre desvio-padrão

Resumo sobre desvio-padrão

• O desvio-padrão é uma medida de dispersão (variabilidade).

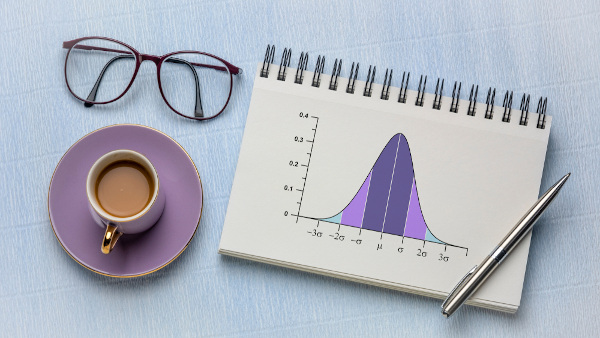
• A letra minúscula sigma (σ) e a letra s são utilizadas para representar o desvio-padrão.

• A letra minúscula um (μ) é utilizada para representar a média aritmética.

• A maior parte dos dados se encontra no intervalo [μ – σ, μ + σ].

• O desvio-padrão corresponde à raiz quadrada da variância, outra medida de variabilidade.

O que é desvio-padrão?

O desvio-padrão é uma medida de dispersão (ou variabilidade). Essa medida indica como os dados variam em relação à média aritmética.

Exemplo:

Em um campeonato de basquete, Ana e Rebeca disputavam quem realizaria o maior número de cestas. Após cinco jogos, o placar foi o seguinte:

Como as duas marcaram a mesma quantidade de cestas (65), a vencedora foi a jogadora mais regular durante o campeonato.

Essa regularidade é determinada pelo desvio-padrão, como veremos adiante. Antes, no entanto, é necessário mencionar um conceito muito próximo do desvio-padrão, chamado de variância.

Diferenças entre desvio-padrão e variância

O desvio-padrão é obtido com base na raiz quadrada da variância. A variância (σ²) determina a variabilidade de um conjunto de dados pela seguinte expressão:

\(σ^2=\frac{∑_{i=1}^N(x_i-μ)^2 }N\)

• N → quantidade de dados

• μ → média aritmética dos dados

• \(∑_{i=1}^N(x_i-μ)^2 \) → \((x_1-μ)^2+(x_2-μ)^2+(x_3-μ)^2+ ...+(x_N-μ)^2\)

• \(x_1,x_2,x_3,…,x_N\) → dados

Apesar da escrita matemática parecer difícil, as contas e a interpretação do resultado são mais simples, como estudaremos a seguir.

Vamos voltar ao exemplo do campeonato de basquete e calcular a variância do número de cestas marcadas para cada jogadora. Para calculá-la, calcularemos a média aritmética para cada uma:

Ana: \(\frac{12+10+13+15+15}5 =13\)

Rebeca: \(\frac{15+11+10+12+17}5 =13\)

Como era esperado (considerando que ambas realizaram 65 cestas em cinco jogos), a média das duas jogadoras é a mesma: 13 cestas. Agora, vamos calcular a variância de cada uma:

Ana: \( σ^2=\frac{(12-13)^2+(10-13)^2+(13-13)^2+(15-13)^2+(15-13)^2}5=\frac{18}5=3,6\)

Rebeca: \(σ^2=\frac{(15-13)^2+(11-13)^2+(10-13)^2+(12-13)^2+(17-13)^2}5=\frac{34}5=6,8\)

Observe que há uma questão com esses resultados. Como o cálculo da variância envolve elevar a diferença entre os dados e a média ao quadrado, a unidade “número de cestas” aparece ao quadrado. Para resolver esse detalhe, observaremos o desvio-padrão para cada uma das jogadoras, que, como sabemos, é justamente a raiz quadrada da variância:

Ana: \( σ=\sqrt[2]{3,6}≅1,9\)

Rebeca: \( σ=\sqrt[2]{6,8}≅2,6\)

Assim, ao longo dos cinco jogos, a maior parte do número de cestas de Ana variou 1,9 (para mais ou para menos) em torno da média 13, ou seja, entre \(13-1,9=11,1\) e \(13+1,9=14,9\).

Já no caso de Rebeca, ao longo dos cinco jogos, a maior parte do número de cestas variou 2,6 (para mais ou para menos) em torno da média 13, ou seja, entre \(13-2,6=10,4 \) e \(13+2,6=15,6\).

Portanto, por apresentar o menor desvio-padrão, a jogadora mais regular foi Ana.

Como se calcula o desvio-padrão?

Considerando um grupo de dados não agrupados de uma população, o desvio-padrão (σ) é calculado pela seguinte expressão:

\(σ=\sqrt[2]{\frac{∑_{i=1}^N(x_i-μ)^2 }N}\)

• N → quantidade de dados

• μ → média aritmética dos dados

• \(∑_{i=1}^N(x_i-μ)^2 \) → \((x_1-μ)^2+(x_2-μ)^2+(x_3-μ)^2+ ...+(x_N-μ)^2\)

• \(x_1,x_2,x_3,…,x_N\) → dados

Exemplo:

José e Fabiano estão concorrendo a um prêmio pela melhor performance escolar na disciplina de História. Durante o bimestre, ambos realizaram três provas e obtiveram as seguintes notas:

Como a média das notas dos dois estudantes foi a mesma, o prêmio foi destinado ao aluno com menor variabilidade de notas. Quem foi o vencedor?

Resolução:

Perceba que o vencedor foi o estudante com menor desvio-padrão. Assim, precisamos inicialmente calcular as médias:

José: \(\frac{10+9,4+9,7}3 = \frac{ 29,1}3=9,7\)

Fabiano: \(\frac{9,6+9,5+10}3 = \frac{29,1}3=9,7\)

Observe que, como informado no enunciado, as médias dos dois alunos são iguais.

Agora, podemos encontrar o desvio-padrão de cada um:

José: \( σ=\sqrt[2]{\frac{(10-9,7)^2+(9,4-9,7)^2+(9,7-9,7)^2}3}≅0,245\)

Fabiano: \(σ=\sqrt{\frac{(9,6-9,7)^2+(9,5-9,7)^2+(10-9,7)^2}3} ≅0,2\)

Portanto, Fabiano foi o estudante que recebeu o prêmio.

Tipos de desvio-padrão

O desvio-padrão está relacionado com o tipo de informação trabalhada e com a organização dos dados. Desse modo, o tipo de desvio-padrão é definido de acordo com os dados trabalhados. Nos exemplos anteriores, tratamos de dados não agrupados de uma população e, portanto, calculamos o desvio-padrão populacional.

Se os dados trabalhados fossem de outro tipo (como dados agrupados) ou estivessem escritos de outra maneira (como no caso de dados agrupados em classes), a expressão do desvio-padrão deveria ser adaptada.

Veja também: Estatística no Enem — como esse tema é cobrado?

Exercícios resolvidos sobre desvio-padrão

Questão 1

(FGV) Considere as duas listas de números a seguir.

Lista 1: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11

Lista 2: 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15

Sejam \(D_1\) e \(D_2\) os desvios-padrões das listas 1 e 2 respectivamente. É correto concluir que:

A) \( D_1=D_2\)

B) \( D_2=D_1+4\)

C) \( D_2=D_1+2\)

D) \( D_2=2D_1\)

E) \( D_2=\sqrt{2D_1}\)

Resolução:

Alternativa A

Sejam \(μ_1\) e \(μ_2\) as médias das listas 1 e 2, respectivamente, e sejam \(σ_1\) e \(σ_2\) os desvios-padrões. Observe que \(μ_1=6\) e \(μ_2=10\). Assim, temos as seguintes expressões para \(σ_1\) e \(σ_2\) (perceba que \((-2)^2=4 \) e \(2^2=4\)):

\(σ_1= \sqrt[2]{\frac{(1-6)^2+(2-6)^2+(3-6)^2+(4-6)^2+(5-6)^2+(6-6)^2+(7-6)^2+(8-6)^2+(9-6)^2+(10-6)^2+(11-6)^2}{11}}\)

\(σ_1= \sqrt[2]{\frac{5^2+4^2+3^2+2^2+1^2+0^2+1^2+2^2+3^2+4^2+5^2}{11}}\)

\(σ_2= \sqrt[2]{\frac{(5-10)^2+(6-10)^2+(7-10)^2+(8-10)^2+(9-10)^2+(10-10)^2+(11-10)^2+(12-10)^2+(13-10)^2+(14-10)^2+(15-10)^2}{11}}\)

\(σ_2= \sqrt[2]{\frac{(5^2+4^2+3^2+2^2+1^2+0^2+1^2+2^2+3^2+4^2+5^2}{11}}\)

Portanto, \(D_1\)=\(D_2\).

Questão 2

(Enem) O procedimento de perda rápida de “peso” é comum entre os atletas dos esportes de combate. Para participar de um torneio, quatro atletas da categoria até 66 kg, Peso-Pena, foram submetidos a dietas balanceadas e atividades físicas. Realizaram três “pesagens” antes do início do torneio. Pelo regulamento do torneio, a primeira luta deverá ocorrer entre o atleta mais regular e o menos regular quanto aos “pesos”. As informações com base nas pesagens dos atletas estão no quadro.

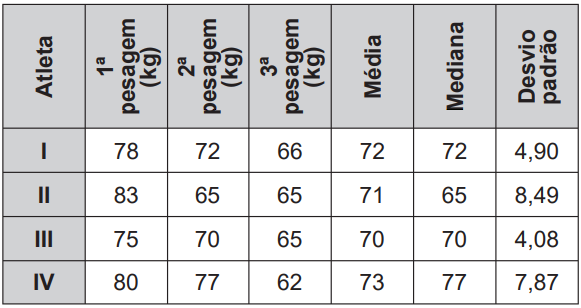
Após as três “pesagens”, os organizadores do torneio informaram aos atletas quais deles se enfrentariam na primeira luta. A primeira luta foi entre os atletas:

A) I e III

B) I e IV

C) II e III

D) II e IV

E) III e IV

Resolução:

Alternativa C

Como a primeira luta ocorre entre o atleta mais regular e o menos regular, os organizadores devem escolher, respectivamente, os atletas com menor e maior desvio-padrão. Assim, segundo a tabela, a primeira luta acontece entre os atletas III e II.