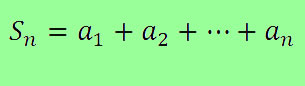A fórmula para soma dos termos de uma Progressão Aritmética (PA) é bastante conhecida e apenas multiplica metade do número de termos de uma PA pela soma de seus termos inicial e final. A demonstração dessa fórmula envolve justamente algumas somas de termos, partindo de um princípio matemático percebido primeiro por Gauss.
Soma de Gauss
Quando criança, Gaus e sua turma na escola foram castigados por um professor: deveriam somar todos os números de 1 a 100. Como bom matemático que já era aos dez anos de idade, Gauss levou poucos minutos para encontrar o resultado 5050 e foi o único a acertar.
Gauss conseguiu esse feito por perceber que a soma dos extremos 1 e 100 é igual a 101, a soma do segundo com o penúltimo termo também é 101 e a do terceiro com o antepenúltimo também. Gauss simplesmente supôs que todas as somas dariam 101 e multiplicou esse resultado por metade do número de elementos da sequência, pois, como estava somando dois a dois, obteria 50 resultados iguais a 101.
Com isso, foi possível criar a seguinte regra:
Em uma PA, a soma dos termos equidistantes das extremidades tem o mesmo resultado que a soma das extremidades.
Demonstração da soma dos termos da PA
Tendo em vista que, somando termos equidistantes das extremidades, o resultado será o mesmo, podemos tomar uma PA de n termos e somar cada termo com sua extremidade. Assim, dada a PA (x1, x2, … ,xn-1, xn), a soma de seus termos é:
Sn = x1 + x2 +… +xn-1 + xn
Agora, a partir da mesma soma, mas com os termos invertidos:
Sn = x1 + x2 +… +xn-1 + xn
Sn = xn + xn – 1 +… +x2 + x1
Observe que os termos opostos já estão um abaixo do outro, mas nós duplicaremos o número de termos ao somarmos essas duas expressões. Portanto, diferentemente de Gauss, obteremos o dobro de uma soma:
Sn = x1 + x2 +… +xn-1 + xn
+ Sn = xn + xn – 1 +… +x2 + x1
2Sn = (x1 + xn) + (x2 + xn-1) +… + (xn-1 + x2) + (xn + x1)
O dobro da soma de Gauss é exatamente o número de termos da PA. Como todas as somas acima são iguais à soma dos extremos, faremos essa substituição e reescreveremos a soma como uma multiplicação:
2Sn = (x1 + xn) + (x2 + xn-1) +… + (xn-1 + x2) + (xn + x1)
2Sn = (x1 + xn) + (x1 + xn) +… + (x1 + xn) + (x1 + xn)
2Sn = n(x1 + xn)
Encontramos o dobro da soma pretendida. Dividindo a equação por 2, teremos:
2Sn = n(x1 + xn)
Sn = n(x1 + xn)
2
Essa é a fórmula usada para a soma dos termos de uma PA.
Exemplo:
Dada a P.A. (12, 24, …), calcule a soma dos seus 72 primeiros termos.
A fórmula para o cálculo da soma dos termos de uma PA depende do número de termos da PA (72), do primeiro termo (12) e do último, que não sabemos. Para encontrá-lo, utilize a fórmula do termo geral de uma PA.
an = a1 + (n – 1)r
a72 = 12 + (72 – 1)12
a72 = 12 + (71)12
a72 = 12 + 852
a72 = 864
Agora, usando a fórmula para soma dos termos de uma PA:
Sn = n(x1 + xn)
2
S72 = 72(12 + 864)
2
S72 = 72(876)
2
S72 = 63072
2
S72 = 31536
Exemplo 2
Calcule a soma dos 100 primeiros termos da PA (1, 2, 3, 4, …).
Já sabemos que o 100º termo da PA é 100. Usando a fórmula par calcular a soma dos termos de uma PA, teremos:
Sn = n(x1 + xn)
2
S100 = 100(1 + 100)
2
S100 = 100(101)
2
S100 = 10100
2
S100 = 5050
Videoaulas relacionadas: